手写LVQ（学习向量量化）聚类算法

LVQ聚类与k-means不同之处在于，它是有标记的聚类。

基本思想：初始化q个原型向量（q代表需要聚类的类别数），每个原型向量也初始化其标签（标签与样本标签取值范围相同），如果原型向量的标签与某样本标签相同/不同，则使用两者间距离更新原型向量（相同时靠近更新，不同时远离更新）。因此，原型向量将反映一个标签的样本与其他标签的样本间的“边界”。训练完毕后，根据样本到原型向量的距离，对样本进行团簇划分。

缺点：因为一般使用欧氏距离，各特征的权重是相同的，无法反映不同特征的重要性差异。

伪代码如下：

 

 python实现如下：

1，算法部分

# 学习向量量化LVQ：有标记的聚类
import numpy as np
import random

def dis(x,y):
    return np.sqrt(np.sum(np.power(x[:-1]-y[:-1],2)))
# lvq算法
def lvq(data,labels,k=4,lr=0.01,epochs=1000,delta=1e-3):
    '''
    data:np.array,last feature is the label.
    labels:1-dimension list or array,label of the data.
    k:num_group
    lr:learning rate
    epochs:max epoch to stop running earlier
    delta: max distance for two vectors to be 'equal'.
    '''
#     学习向量
    q=np.empty(shape=(k,data.shape[-1]),dtype=np.float32)
#     确认是否所有向量更新完了
    all_vectors_updated=np.empty(shape=(k,),dtype=np.bool)
    num_labels=len(labels)
#     初始化原型向量，从每一类中随机选取样本，如果类别数小于聚类数，循环随机取各类别中的样本
    for i in range(k):
        q[i]=random.choice(data[data[:,-1]==labels[i%num_labels]])
    step=0
    while not all_vectors_updated.all() and step<epochs:
#         从样本中随机选取样本，书上是这么写的，为啥不循环，要随机呢？np.random的choice只支持一维
        x=random.choice(data)
        min_dis=np.inf
        index=0
        for i in range(k):
            distance=dis(x,q[i])
            if distance<min_dis:
                min_dis=distance
                index=i
#         保存更新前向量
        temp_q=q[index].copy()
#         如果标签相同，则q更新后接近样本x，否则远离
        if x[-1]==q[index][-1]:
            q[index][:-1]=q[index][:-1]+lr*(x[:-1]-q[index][:-1])
        else:
            q[index][:-1]=q[index][:-1]-lr*(x[:-1]-q[index][:-1])
#         更新记录数组
        if dis(temp_q,q[index])<delta:
            all_vectors_updated[index]=True
        step+=1
#     训练完后，样本划分到最近的原型向量簇中
    categoried_data=[]
    for i in range(k):
        categoried_data.append([])
    for item in data:
        min_dis=np.inf
        index=0
        for i in range(k):
            distance=dis(item,q[i])
            if distance<min_dis:
                min_dis=distance
                index=i
        categoried_data[index].append(item)
    return q,categoried_data
        
    

2，验证、测试

2.1 随机x-y平面上的点，根据y=x将数据划分为2个类别，然后聚类

先看看原始数据分布：

x=np.random.randint(-50,50,size=100)
y=np.random.randint(-50,50,size=100)
x=np.array(list(zip(x,y)))

import matplotlib.pyplot as plt
%matplotlib inline

plt.plot([item[0] for item in x],[item[1] for item in x],'ro')

 

 处理输入数据：

# y>x:1  y<=x:0
y=np.array([ 1&(item[1]>item[0]) for item in x])
y=np.expand_dims(y,axis=-1)
data=np.concatenate((x,y),axis=1).astype(np.float32)

训练，显示结果

q,categoried_data=lvq(data,np.array([0.,1.]),k=4)

color=['bo','ko','go','co','yo','ro']
for i in range(len(categoried_data)):
    data_i=categoried_data[i]
    plt.plot([item[0] for item in data_i],[item[1] for item in data_i],color[i])
plt.plot([item[0] for item in q],[item[1] for item in q],color[-1])
plt.show()

这里执行了2次，可以看出与k-means一样，对初值敏感

 

 

 

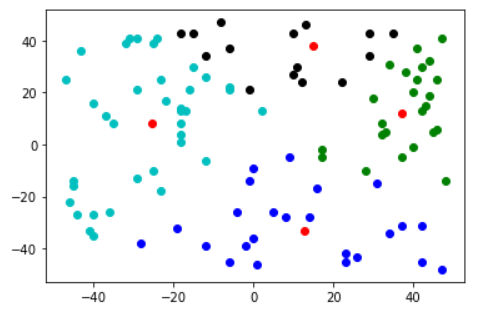
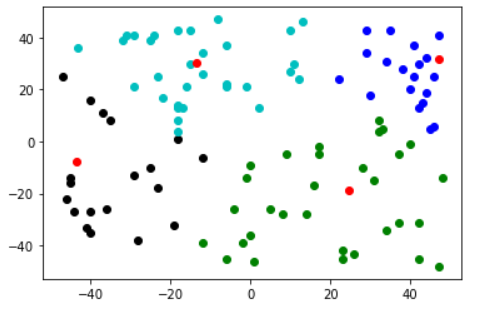
 总结：

根据上图可以看出，聚类的效果是在标记的前提下进行的，即团簇是很少跨过分类边界y=x的。相当于对每一个类别，进行了细分。因为每次训练根据一个样本更新，epochs应该设置大一点。