手写k-means算法

作为聚类的代表算法，k-means本属于NP难问题，通过迭代优化的方式，可以求解出近似解。

伪代码如下：

 

 1，算法部分

距离采用欧氏距离。参数默认值随意选的。

import numpy as np
def k_means(x,k=4,epochs=500,delta=1e-3):
#     随机选取k个样本点作为中心
    indices=np.random.randint(0,len(x),size=k)
    centers=x[indices]
#     保存分类结果
    results=[]
    for i in range(k):
        results.append([])
    step=1
    flag=True
    while flag:
        if step>epochs:
            return centers,results
        else:
#             合适的位置清空
            for i in range(k):
                results[i]=[]
#         将所有样本划分到离它最近的中心簇
        for i in range(len(x)):
            current=x[i]
            min_dis=np.inf
            tmp=0
            for j in range(k):
                distance=dis(current,centers[j])
                if distance<min_dis:
                    min_dis=distance
                    tmp=j
            results[tmp].append(current)
#　　　　　更新中心
        for i in range(k):
            old_center=centers[i]
            new_center=np.array(results[i]).mean(axis=0)
#             如果新，旧中心不等，更新
#             if not (old_center==new_center).all():
            if dis(old_center,new_center)>delta:
                centers[i]=new_center
                flag=False
        if flag:
            break
        # 需要更新flag重设为True
        else:
            flag=True
        step+=1
    return centers,results
                
def dis(x,y):
    return np.sqrt(np.sum(np.power(x-y,2)))

2，验证

我随机出了一些平面上的点，然后对其分类。

x=np.random.randint(0,50,size=100)
y=np.random.randint(0,50,size=100)
z=np.array(list(zip(x,y)))

import matplotlib.pyplot as plt
%matplotlib inline

plt.plot(x,y,'ro')

首先看看未分类之前的，当然也是跟分类后的分布是一样的。

然后看看分类后的结果：

centers,results=k_means(z)

color=['ko','go','bo','yo']
for i in range(len(results)):
    result=results[i]
    plt.plot([res[0] for res in result],[res[1] for res in result],color[i])
plt.plot([res[0] for res in centers],[res[1] for res in centers],'ro')
plt.show()

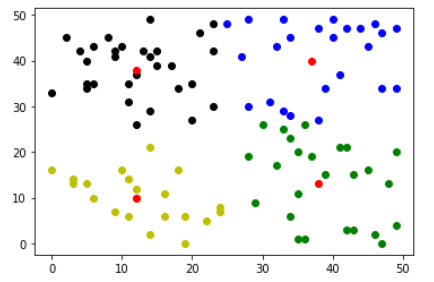
 可以看出，4个分类还是挺合理的。

再增加k=5试试，多执行几次看看。

centers,results=k_means(z,k=5)

color=['ko','go','bo','yo','co']
for i in range(len(results)):
    result=results[i]
    plt.plot([res[0] for res in result],[res[1] for res in result],color[i])
plt.plot([res[0] for res in centers],[res[1] for res in centers],'ro')
plt.show()

 

 

 

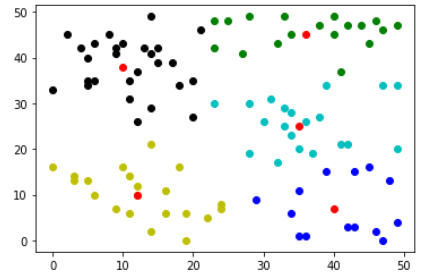
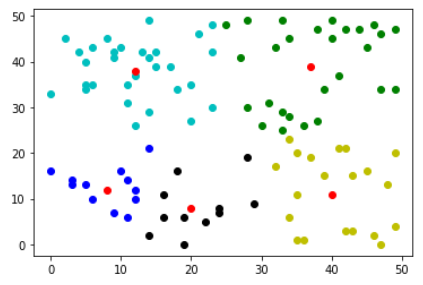
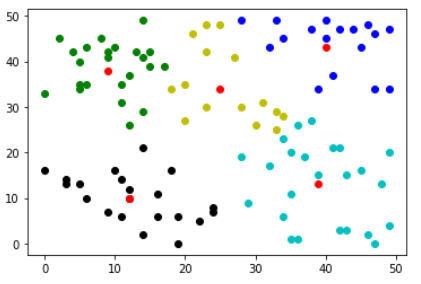
 可以看出，此算法对初值很敏感。

   _^v^_