动态规划经典算法--最长公共子序列 LCS

转移方程

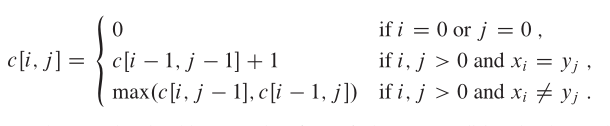
代码：

//法一：
#include <bits/stdc++.h>
using namespace std;
//---------------https://lunatic.blog.csdn.net/-------------------//
int dp[100][100];
string s[100][100];
int main()
{
    string a, b;
    cin >> a >> b;
    dp[0][0] = 0;
    memset(dp, 0, sizeof(dp));
    for (int i = 0; i < a.size(); i++)
        for (int j = 0; j < b.size(); j++)
        {

            if (a[i] == b[j])
            {
                dp[i + 1][j + 1] = dp[i][j] + 1;
                s[i + 1][j + 1] = s[i][j] + a[i];
            }
            else
            {
                if (dp[i + 1][j] > dp[i + 1][j])
                {
                    dp[i + 1][j + 1] = dp[i + 1][j];
                    s[i + 1][j + 1] = s[i+1][j] ;
                }
                else 
                {
                     dp[i + 1][j + 1] = dp[i][j+1];
                    s[i + 1][j + 1] = s[i][j+1]  ;
                }
            }
        }
        cout<<dp[a.size()][b.size()]<<endl;
        cout<<s[a.size()][b.size()];
}

//法二：
#include <bits/stdc++.h>
using namespace std;
//---------------https://lunatic.blog.csdn.net/-------------------//
string a, b;
int dp[100][100];
int c[100][100];
void printAns(int i, int j)
{

    if (i == -1 || j == -1)
        return;
    if (c[i][j] == 0)
    {
        printAns(i - 1, j - 1);
        cout << a[i];
    }
    else if (c[i][j] == 1)
        printAns(i, j - 1);
    else
        printAns(i - 1, j);
}
int main()
{

    cin >> a >> b;
    dp[0][0] = 0;
    for (int i = 0; i < a.size(); i++)
        for (int j = 0; j < b.size(); j++)
        {

            if (a[i] == b[j])
            {
                dp[i + 1][j + 1] = dp[i][j] + 1;
                c[i][j] = 0; //代表相等
            }
            else
            {
                if (dp[i + 1][j] > dp[i + 1][j])
                {
                    dp[i + 1][j + 1] = dp[i + 1][j];
                    c[i][j] = 1; //代表不相等，从上面的不相等
                }
                else
                {
                    dp[i + 1][j + 1] = dp[i][j + 1];
                    c[i][j] = -1; //代表不相等，从左面的不相等
                }
            }
        }
    cout << dp[a.size()][b.size()] << endl;
    printAns(a.size() - 1, b.size() - 1);
    cout << endl;
}