随想随写，写得还是太繁琐了，同时比较仓促，大概率存在叙述上的不周密甚至错漏，请批判看待，欢迎指正。
1.简述充分条件与必要条件
如果只是想判断充分条件/必要条件，那么只要记住下述内容就足够了。
- 若$p \Rightarrow q$，则称$p$是$q$的充分条件，$q$是$p$的必要条件。
- 充要条件：若$p \Leftrightarrow q$，则$p$和$q$互为充分必要条件。
需要强调的一点是，充分条件/必要条件是在同一个推导过程中相伴存在的，如$p \Rightarrow q$伴随着充分条件和必要条件的存在。注意，不要被“条件推结论”这一观点引导，产生“$q$是$p$的必要条件是对应$q \Rightarrow p$这个推导过程”的错误印象。[1]
2.对充分条件和必要条件的理解
除开通过$p \Rightarrow q$形式分辨充分条件/必要条件，其实也可以从更加通用的角度来理解充分条件与必要条件这一对概念。
想象一个开关并联的电路(如图①)和一个开关串联的电路(如图②)[2]
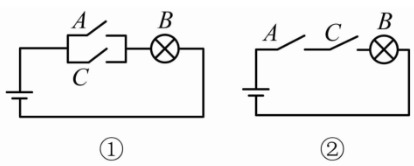
如果我们以灯泡B亮作为结论，为了使得灯泡亮，图①和图②两种电路有不同的选择。
对于图①，开关A与开关C中任一开关关闭，灯泡都会亮。
那么“开关A关闭”或“开关C关闭”，是“灯泡亮”这一结论成立的充分条件。
对于图②，开关A与开关C必须一同关闭，灯泡才会亮。
那么“开关A关闭”或“开关C关闭”，是“灯泡亮”这一结论成立的必要条件。
3.阶段小结
上述两部分内容，展示了两种典型的充分条件/必要条件概念的解释方式。
第一种从$p \Rightarrow q$出发，简明地点出了充分条件和必要条件，第二种从实例出发，说明了充分条件/必要条件与结论之间的关系。
虽然角度不同，但两者实际上是一回事。
以$x^{2}+2x+1 ＞ 4$为例，学过一元二次不等式后很容易解出使得该不等式成立的$x$的取值范围是$x＞1 \cup x<-3$。(容易知道，$x^{2}+2x+1 ＞ 4 \Leftrightarrow x＞1 \cup x<-3$，二者等价)
如果把$x^{2}+2x+1 ＞ 4$作为结论，该结论的必要条件和充分条件是好举例的。
充分条件举例：$x＞1$、$x<-3$、$x<-2$等等。$x＞1 \cup x<-3$的任一子集都是$x^{2}+2x+1 ＞ 4$成立的充分条件。
以$x＞1$为例，$ [1,+\infty] \subset [-\infty,-3] \cup [1,+\infty]$ [例①]
只要满足前者($x＞1$)，必然满足后者($x＞1 \cup x<-3$)，所以$x＞1$是$x＞1 \cup x<-3$充分条件。而如果反过来看，满足$x＞1 \cup x<-3$，不一定就满足$x＞1$，但要满足$x＞1$，必须要满足$x＞1 \cup x<-3$，所以$x＞1 \cup x<-3$是$x＞1$的必要条件。这也就是第一个段落中所说的$p \Rightarrow q$过程伴随者充分条件/必要条件的存在。
必要条件举例：$x \notin [-3,-2]$、$x \notin [-3,-1]$、$x \notin [-2,-1]$等等。只要$x＞1 \cup x<-3$是取到的范围的子集即可。
必要条件也是如此，以$x \notin [-3,-2]$为例，$[-\infty,-3] \cup [1,+\infty] \subset \complement_R[-3,-2]$ [例②]
思路类似于[举例①]，偷个懒，不再说了。
4.再延伸
如果再细致地思考一下第三段落中的举例，会发现充分条件和必要条件可以用集合的关系去表示。
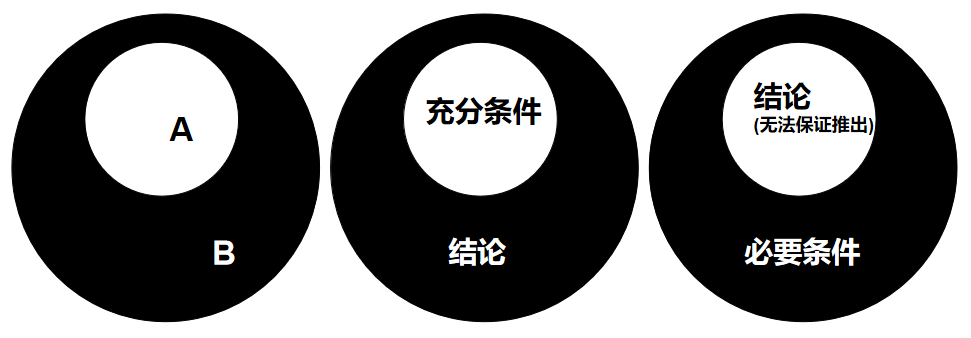
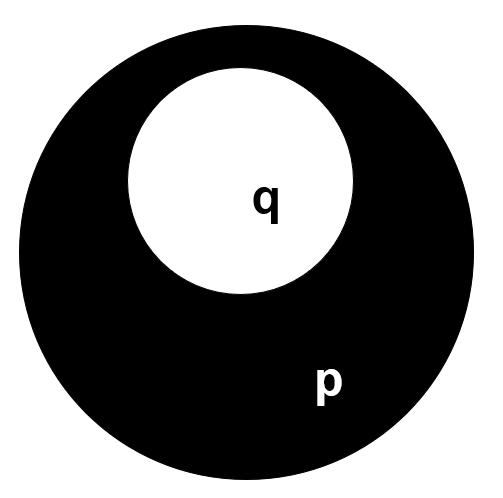
如上图，如果把[例①]以韦恩图的形式展示出来，会发现条件(图中记为区域A)和结论(图中记为区域B)的关系如第一张图所示。
$A \Rightarrow B$则$A$是$B$的充分条件，$B$是$A$的必要条件。
从图中可以观察到的一些细节：充分条件的取值范围是小于等于结论恰好成立的取值范围的(即子集)。与结论恰好成立所需要的条件相比来说，充分条件显得太充分了(条件限制太多)，所以只要符合充分条件，就一定能使得结论成立，就像第二张图中，如果一个点出现在白色圆中，这个点必然也在外部的黑色圆之中。
但如果想要站到黑色圆内，却不一定需要在白色圆内：以站在黑色圆内为目的，除了白色圆内还有很多区域，这些区域都是站在黑色圆内的充分条件(所以充分条件是不唯一的，而且同一个结论的不同充分条件之间的交集可以为空。)
对所有的充分条件取并集(满足其一即可)的结果，就是使得结论恰好成立的条件。(所以其实最大的充分条件[3]，就是使得结论恰好成立的条件。)
而对于必要条件来说，即使是已经符合了必要条件，也不能确保结论(这个结论不是上面充分条件讨论中的结论)成立，就像第三张图中，站在黑色圆内并不能保证站在白色圆内，但如果不在黑色圆内，那么一定不在白色圆内。
和充分条件一样，一个结论的必要条件也不是唯一的，只要包含结论的条件都是必要条件。
而想要使得结论成立，必须满足所有的必要条件。也就是对所有必要条件取交集。(所以其实最小的必要条件[3]，就是使得结论恰好成立的条件。)
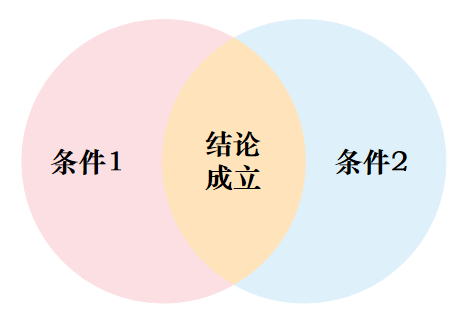
在涉及必要条件这一概念时需要注意的一点是，单个必要条件往往是不能确保结论成立的。
5.充分必要条件与充分性、必要性
在第四自然段中提到了最大的充分条件和最小的必要条件[3]，对于同一个$p \Rightarrow q$过程来说，最大的充分条件和最小的必要条件是相同的，此时条件圆和结论圆完全重叠，$q \Rightarrow p$成立。
因而有$p \Leftrightarrow q$，$p$与$q$互为充分必要条件。
这里涉及了四个新的概念：充分必要条件、 既不充分也不必要条件、充分不必要条件、必要不充分条件。
虽然乍看起来是全新的概念，但实际上在第三四段的讨论中，对此已有所涉及。
首先要明确的是充分条件/必要条件和这四个新的概念的关系。
在第一段内容中已经说明，$p \Rightarrow q$伴随着充分条件和必要条件的存在，而一个推导过程也只有一对充分条件/必要条件。
如在$p \Rightarrow q$过程中，$p$是$q$的充分条件，$q$是$p$的必要条件，这一过程中，是不会有“$p$是$q$的必要条件，$q$是$p$的充分条件”的说法的。
而“$p$是$q$的必要条件，$q$是$p$的充分条件”这种表述对应的是$p \Leftarrow q$(即$q \Rightarrow p$)这一过程中。
也就是说，充分必要条件、 既不充分也不必要条件、充分不必要条件、必要不充分条件包括了对$p \Rightarrow q$和$q \Rightarrow p$两个过程的描述，两两组合如下表：
| $p \Leftarrow q$ | $p \nLeftarrow q$ | |
| $p \Rightarrow q$ |
$p \Leftrightarrow q$ $p$是$q$的充分必要条件 $q$是$p$的充分必要条件 |
$p \Rightarrow q,p \nLeftarrow q$ $p$是$q$的充分不必要条件 $q$是$p$的必要不充分条件 |
| $p \nRightarrow q$ |
$p \nRightarrow q,p \Leftarrow q$ $p$是$q$的必要不充分条件 $q$是$p$的充分不必要条件 |
$p \nLeftrightarrow q$ $p$是$q$的既不充分也不必要条件 $q$是$p$的既不充分也不必要条件 |
可以看到的是必要不充分条件-充分必要条件-充分不必要条件对应$p$圆和$q$圆的关系与第四段的图示形式上是一致的，只不过在第四段中出现时只针对$p \Rightarrow q$过程而这里是同时对$p \Rightarrow q,q \Rightarrow p$两个过程。而判定到底属于哪一类条件，也取决于叙述，”$p$是$q$“和”$q$是$p$“会有不同的结果(但两者之间也存在联系)。
与之相关的一组概念是充分性和必要性。在充分必要条件证明题中常见。充要条件证明的表述通常分为“1)A的充要条件是B。2)A是B的充要条件。”两种。
请注意这两种表述中谁是条件谁是结论。前者B是条件A是结论，后者A是条件B是结论。
条件推结论是证明充分性，结论推条件是证明必要性。
6.注释与参考文献
[1]如果$q \Rightarrow p$，说明q是p的充分条件。只是必要条件是无法保证一定推出结论的，所以必要条件A一般不能写成$A \Rightarrow …$的形式。
[2]车慧,钱军先.稚化教师的思维,促进学生的理解——从“充分条件和必要条件”的三次设计谈数学概念教学[J].中学数学月刊,2016(02):27-29.
