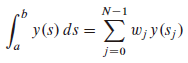[摘记]数值方法14——积分方程和反演理论
注:以下来自《C++数值算法一书》,仅对章节内容做摘要,为的是给自己扫盲,不涉及算法。
Fredholm方程涉及具有固定上、下限的定积分。第一类非齐次Fredholm方程形式如下:
K(t,s)称为核,上式对应的矩阵方程为Kf=g。第一类方程是病态的,核作用到一个函数通常起到光滑的作用,会丢失信息,这类问题专门的处理方法是反演问题。
第二类Fredholm方程写为:
没有特别的病态。
Volterra方程是Fredholm的一种特殊形式,去除不必要的积分部分,将积分上限改为自变量t的形式。第一类Volterra方程:
第二类Volterra方程写为
1. 第二类Fredholm方程
要求f(t)使用的方法称为Nystrom方法,这是一个非常基本的方法:
wj是积分法则的权,N点sj集是横坐标。这里倾向于用高阶积分法以保持N尽可能小。对于光滑、非奇异问题,最好的是高斯积分。
2. Volterra方程
Volterra方程的大部分算法从t=a开始,随着不断地迭代逐渐求出解。最简单的方法是在均匀步长的网格上用梯形法则。
对于高阶方法,目前认为最好的是逐块法。
3. 具有奇异核的积分方程
深入讨论略
4. 反演问题与先验信息的利用
我完全看不懂= =,甚至提到了哲学思想0 0
5. 线性正则化方法
又称为Phillips-Twomey方法、约束线性反演方法等。对之前的反演方法做了些改进,是本书推荐的方法。
6. Backus-Gilbert方法
与上一个方法相比,致力于提高稳定性而不是注重光滑性。
7. 最大熵图像恢复
反演问题涉及到的概率问题在这里发挥到了极致,还有哲学思想、历史性。。。。请恕我理解无能
这章可以说完全看不懂,慎入= =
本文原创,转载请注明出处