[摘记]数值方法13——两点边值问题

注：以下来自《C++数值算法一书》，仅对章节内容做摘要，为的是给自己扫盲，不涉及算法。

当微分方程要求在多于一个的自变量值上满足边界条件时，这种问题叫做两点边值问题。解两点边值问题有两种不同类型的数值解法：打靶法和松弛法

 

1. 打靶法

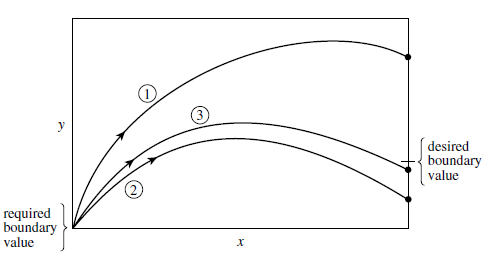
打靶法的积分过程是从x₁到x₂，并且努力使积分结果在积分的终点和边界条件匹配。在一个边界x₁上选择了所有因变量的值，这些值必须和该边界的边界条件保持一致。而另一个边界x₂上的因变量依赖于随机猜测的参数。在迭代过程中，渐渐地接近真实值，就像打靶一样。打靶法适合于解震荡的很厉害的情况，精确地运用了多维全局收敛Newton-Raphson，设法零化n₂个变元的n₂个函数，这些函数通过从x₁到x₂积分N个微分方程得到。

 

2. 对拟合点打靶

有时，由于错误严重的起始条件，初始解从x₁到x₂要碰到某些不可计算的，或是灾难性的结果。拟合点打靶首先从x₁积分到x₁和x₂之间的一个点x_f，然后再从x₂反向积分到x_f。

 

3. 松弛法

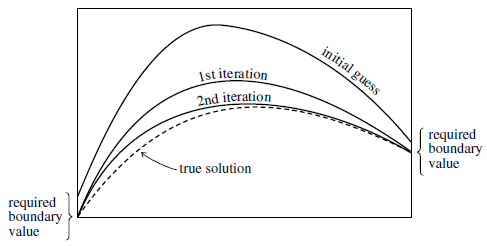
松弛法用了另外一种逼近方法，微分方程由覆盖积分限的一系列有限个差分方程来替代，试验解由各个网格点上的因变量的值组成，并不满足所需的有限个差分方程和边界条件。迭代调整所有在网格上的值，使他们满足各个联系的差分方程，也满足边界条件。适用于解平滑的情况，需要良好的初始预测值。

 

深入讨论略

本文原创，转载请注明出处

http://www.cnblogs.com/luluathena/