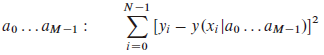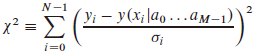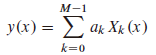[摘记]数值方法11——数据建模
注：以下来自《C++数值算法一书》，仅对章节内容做摘要，为的是给自己扫盲，不涉及算法。
给定一组观察结果，我们经常要对这组数据进行浓缩和概括，使它适合依赖于可调整参数的模型。基本方法是选择或设计一个优值图形函数，它必须能度量数据和具有特别参数选择的模型之间一致性的程序。接着，对模型的参数进行调节，使优值函数取最小值，产生最佳拟合参数。
参数拟合不是一个参数估计的终结。一个真正有用的拟合过程必须提供：1参数；2参数的误差估计；3拟合优度的统计度量；如果3中的结果表明这种模型不和数据一致，那么1和2的结果几乎没有价值。
1. 最大似然估计的最小二乘法
假定用具有M个可调参数
的模型来拟合N个数据点
。这个模型给出了已测自变量和因变量之间的一个函数关系：
通过对a的最小二乘方拟合，求：
如果每个数据点都有它自己已知的标准差，则可以用χ2拟合。
2. 拟合数据成直线
这个问题被称为线性回归，用N个数据点拟合成直线模型：
然后可以用χ2拟合来确定a和b。
3. 一般的线性最小二乘方
上一个问题的推广是x的任意M个特定函数的线性组合，得到一般形式的多项式：
其中Xk(x)可以是x的非线性函数。
为了寻求使χ2最小化的最佳参数，引入一个设计矩阵A：
再引入向量b：
然后可以用正规方程组或者奇异值分解法来求解。
4. 非线性模型
在非线性依赖情况下，求最小值必须迭代进行。当非常接近极小值时，我们希望χ2函数趋近于二次型，可以将它写为
其中，d是长度为M的向量，而D是M*M的矩阵。如果这种近似是一种很好的近似，则可以用一步得到最小值：
如果这是一个比较差的近似，首先要做的是沿负梯度方向走一步：
为了利用上面两个式子，必须求得χ2函数的梯度和二阶导数矩阵（黑塞矩阵）D。
Levenberg-Marquardt方法能够在上面两个公式之间光滑地变动，在实际应用中非常有效。
5. 被估模型参数的置信界限
这里的目的是为了知道参数集与真实参数值的差
的分布，在不知道真实参数值以及不可能获得假设数据集的无穷多个全域时，寻找估计或近似
的概率分布的方法。有一种常用的方法蒙特卡罗模拟用a(0)替代atrue。
6. 稳健估计
有时候实验误差会对估计结果造成很大的影响，中位数对中心值的估计比均值更稳健。稳健估计可以分为三类：M估计由最大似然论述得出，是参数的估计关系最密切的一类，依据测量误差的分布，选择合适的公式去计算参数；L估计是“顺序统计量的线性组合”；R估计是建立在秩检验上的估计，例如两个分布的相等或者不等可以用Wilcoxon检验来估计。
本文原创，转载请注明出处
