[摘记]数值方法07——求根与非线性方程组
注:以下来自《C++数值算法一书》,仅对章节内容做摘要,为的是给自己扫盲,不涉及算法。
第8章排序是算法导论说过的,大家都知道的算法。也是我看的最轻松的。。。。略
除线性情况外,求根过程总要借助迭代来完成,在一维和多维情况下都是如此。常用的算法总是从某个近似的初始解出发,不断修改这个解,直到满足某种预先确定的收敛准则位置。
1. 划界与二分
思想:如果f(a)与f(b)具有相反的符号,则我们认为将有一根被划界在区间(a,b)内,又若函数是连续的,则至少有一个根必落在该区间内(中值定理)。一旦知道了某个区间内包含有方程的一个根,则计算函数在该区间中点的值,并考察起符号,用中点替代与它具有相同函数符号的端点。每次迭代都将包含根的区间减少一半。
2. 弦截法、试位法和Ridders方法
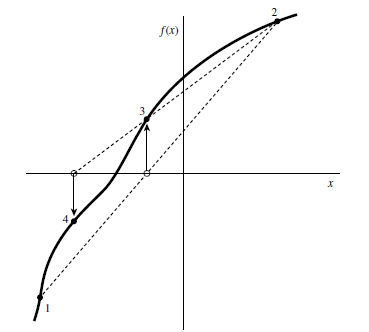
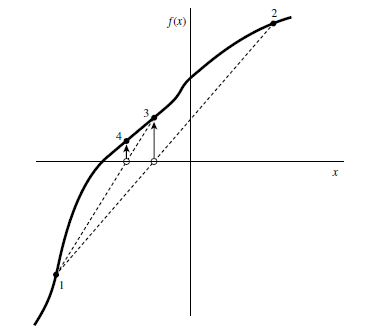
思想:对于在根附近光滑的函数,弦截法、试位法收敛速度通常快于二分法。感觉图示会比较直观:
图左为弦截法,每次更新左右区间,图中为[1,2]->[3,4];图右为试位法,每次仅更新区间端点之一,图中为[1,2]->[1,3]->[1,4]
Ridders方法对试位法进行了极有益的改进,使用特定的函数计算出修正过的x3和x4,加速迭代。
3. Van Wijngaarden-Dekker-Brent方法
Brent方法既能够超线性收敛,又不失二分法的确定性。它将根的划界、二分法以及二次反插值方法相结合。二次反插值是用3个估值点拟合一个二次反函数(x作为y的二次函数),该函数在y=0处的值将作为根x的下一估值。对只知函数值(而不可求其导数或函数的形式)的一般一元方程的求根,建议用此方法。
4. 利用导数的Newton-Raphson方法
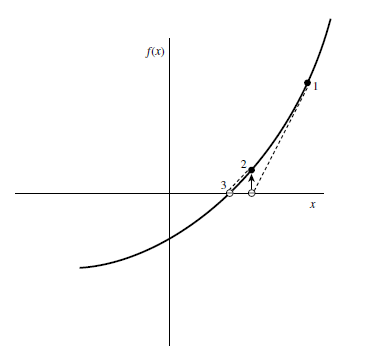
还是上图吧,求点1的切线与x轴交点,投影到函数得到点2,依此类推。这是一种很有效率的方法,达到了二次收敛。但有可能死于局部极值的状况,这时会无法收敛。可以与二分法结合,摆脱这种困境。
5. 多项式的根
我们知道n阶多项式有n个根,可能是实数也可能是复数,或者有重根。多项式的降阶可以大大减少计算量,但需谨慎使用,以免误差太大。如果要获取复根,可以参考Muller方法、拉盖尔方法等。
6. 非线性方程组的Newton-Raphson方法
对于含1个以上线性方程的方程组,目前还没有一种好的一般性解法。Newton-Raphson方法是多维求根方法里最简单的一种,对于足够好的初值,收敛效果很明显。
深入讨论略
本文原创,转载请注明出处