[读书笔记/翻译]Multiple View Geometry in Computer Vision-1.2,1.3
1.2 Camera projections
点镜头 投影其实是一个降维的过程,通常是将3D的事物用2D的图像表示出来。下面介绍中心投影(centre projection),空间中的点经过一个固定点(投影中心)延伸出的射线。这个射线与图像平面的交点就是点的图像。
注:听起来像小孔成像。。。具体的还是看书上的截图吧,我这里是扫描版不清楚,就不贴出来了。
如果空间上的点共面,则这个面与图像平面存在投影转换;所有的从同一镜头中心投影过来的图像都跟一个投影转换相关。其实前两条的原理是一样的,以为这些面都是穿过同一中心的光线的映射。
穿过(0,0,0,1)的点(X,Y,Z,T)的射线可以用(X,Y,Z)表示,可以看出对任何常量k,k(X,Y,Z)都表示同样的射线。因此所有的射线都用齐次坐标表示。事实上它们构成了射线的2D空间。来自同一中心的不同投影所产生的图像格式差异就是由形成光线的集合决定的。简单来说,同一镜头中心生成的图像是等价的。
Calibrated cameras 对于3D世界的欧式几何,需要在投影空间指定一个特殊的无穷远平面和一个特定的平面上的二次曲面作为绝对二次曲线来决定的(这句翻译的不好,详见1.1)。如果镜头不在这个平面上,则平面与图像平面上有一一对应的映射。因为图像上的任何点都被定义为在空间中有一条线与无穷远平面相交在一个点。而绝对二次曲线一定在图像上有一个二次曲线的投影。这个图像曲线被称为IAC(Image of the Absolute Conic)。如果图像上IAC的位置已知,则我们说镜头是calibrated。(WIKI了一下没找到Calibrated camera的概念,但有Camera Calibration,对于给定的照片,找出镜头的参数。)
Calibrated camera可以确定图像上两个点的投影射线的夹角。 已知空间中的两条线的夹角取决于相对于绝对二次曲线它们在哪与无穷远平面相交。在Calibrated camera中,由于存在一一对应,两个图像点与IAC w之间的投影关系就等于它们在空间的射线与无穷远平面的交叉和绝对二次曲面的关系。因此,已知IAC,我们可以直接测量图像来得到射线的夹角。可以通过image patch来计算视野表现的区域,决定图像上的一个椭圆能否逆投影到一个圆锥。后面就可以看到,这有助于决定一个重建场景的欧式结构。
注:以上说的是能否通过一张图像来重建场景。
传统的重建技术分析平行线的特征和灭点来决定场景的仿射结构(累死于绘画时先确定水平线,然后画出透视关系线条这样一个过程的逆过程)。这样一个过程尚且不能成为全自动的,但投影集合知识可以用于用户指导的单视点重建场景系统中。
1.3 多视点重建
接下来首先讨论两幅图像的重建。考虑一个集合xi <-> xi’,对应两幅图像。假定存在镜头矩阵P和P’以及3D点的集合Xi。PXi=xi,P’Xi=xi’。镜头矩阵和3D点都不是已知,需要由我们来决定。
很明显点的位置不能被唯一确定,即使给出一个立方体的几幅图,还是不能确定它的绝对位置、朝向和大小。重建只能说是得到世界的相似转换,除非已知两个镜头的calibration,才能用投影转换这种更一般的转换来表达重建。假设投影转换是一个4*4的矩阵H:
H的选择是随意的,我们说这个重建具有投影随意性,或者说是一个投影重建。这是最坏的情况。两幅图片的点集合重建的基本工具是基础矩阵,表现了图像点的约束。这个约束起源于两个视点的镜头中心与图像点、空间点的共面性。给定基础矩阵F(3*3的二阶矩阵,可以由点计算出来),点xi <-> xi’必须满足:
镜头矩阵P和P'唯一地决定了基础矩阵F,反之,基础矩阵决定了一对镜头矩阵,取决于3D投影随意性。因此投影矩阵封装了两个镜头的完整投影几何,不随3D投影转换而改变。基础矩阵重建场景的算法很简单,以下是它的提纲:
- 给定对应两个视点的点集合,根据共面方程
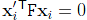 形成F的元的线性方程式。
形成F的元的线性方程式。 - 根据线性方程组的解得出F。
- 根据9.5节中的公式计算两个镜头矩阵。
- 已知镜头矩阵和对应的镜头点,计算3D点。这个方法被称为三角测量法(triangulation)。
本文原创,转载请注明出处:



