前缀和与差分

前缀和

其实可以把它理解为数学上的数列的前n项和（对于一个一维数组的前缀和）。

我们定义对于一个数组a的前缀和数组s，s[i] = a[1]+a[2]+...+a[i].

 

二维前缀和

与一维前缀和类似，设s[i][j]表示所有a[i'][j']的和。（1≤i'≤i,1≤j'≤j）

有一点像“矩形的面积”那样，把一整块区域的值都加起来。

 

前缀和的用途

一般用来求区间和。

对于一维情况，现在我给出一个数列a，要求你回答m次询问，每次询问下标j到k的和。朴素的做法显然是对于每次询问都执行一次相加操作，然后输出结果。这样做是正确的，但是当m过大时就会导致计算次数过多而有可能超时。

超时的原因一目了然，重复计算。那么我们应该怎么改进这个方法呢？想象一下，我们如果先提前算好了每一个位置的前缀和，然后用s[k]-s[j]，结果不就是我们这次询问的答案吗？这样便会使计算量大大减小。

对于二维的区间和，也是类似的。

 

我们借助这个图片研究一下。假设在这个矩阵（二维数组）中，我们要求和的是上图中红色区域。现在我们已经预处理出了所有点的前缀和，现在给定两个点（x1,y1），（x2,y2），我们要求 以这两个点连线为对角线的一个子矩阵的数值之和。暴力做法直接挨个加这个我就不再多说了，反正早晚都得TLE，我们重点考虑用前缀和的快速做法。

首先我们可以把s[x2][y2]求出来，它代表整个大矩形的前缀和，然后我们分别减去它左边多出来的一块的前缀和和下边多出来一块的前缀和，这样就是最终答案了？

不是！这不是最终答案。可以发现，在我们剪掉这两个多出的区域时，下边的一小块被减了两次，但减两次显然是不合理的，我们应该加回来。。

所以对于一次的查询答案ans应该等于s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]。

这个二维前缀和也称差分序列。

 

用差分实现区间操作

给定一个长度为n的数列a，要求支持操作add(L,R,k)表示对a[L]~a[R]的每个数都加上k。并求修改后的序列a。

暴力做法显然，TLE，下一个。

我们考虑用差分的做法。这里 需要一个辅助数组c，c用来记录某一个位置上的总改变量。c[i]表示的是i~n这些元素都加上c[i]这个数。我们对[L,R]区间进行加值操作，在c[L]处加一个k，在c[R+1]处就减去一个k。最后求序列的每个位置变成了多少，只需要求一下c数组的前缀和，然后和原数组按位相加就好。

这个结论的证明我不是太会。。呃记住它是对的就好啦。。

对于二维的情况，一个n*m的矩阵，要求支持操作add(x1,y1,x2,y2,a)，表示对于以(x1,y1)为左下角，(x2,y2)为右上角的矩形区域，每个元素都加上a。要求修改后的矩阵。

我们的做法和一维类似。用数组c存储总改变量。在c[x1][y1]处加上a，在c[x2+1][y1]和c[x1][y2+1]处减a，在c[x2+1][y2+1]再加上a。最后(i,k)位置上的数值就是c数组在(i,k)位置的前缀和。

 

差分

用差分实现区间操作

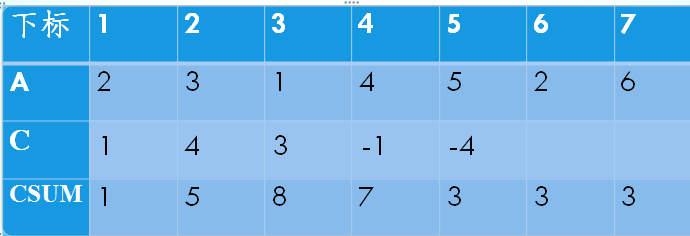
取C数组为修改数组，C[i]表示的是i~n这些元素都加上C[i]这个数
样例：
ADD(1,3,1)
ADD(2,4,4)
ADD(3,7,3)
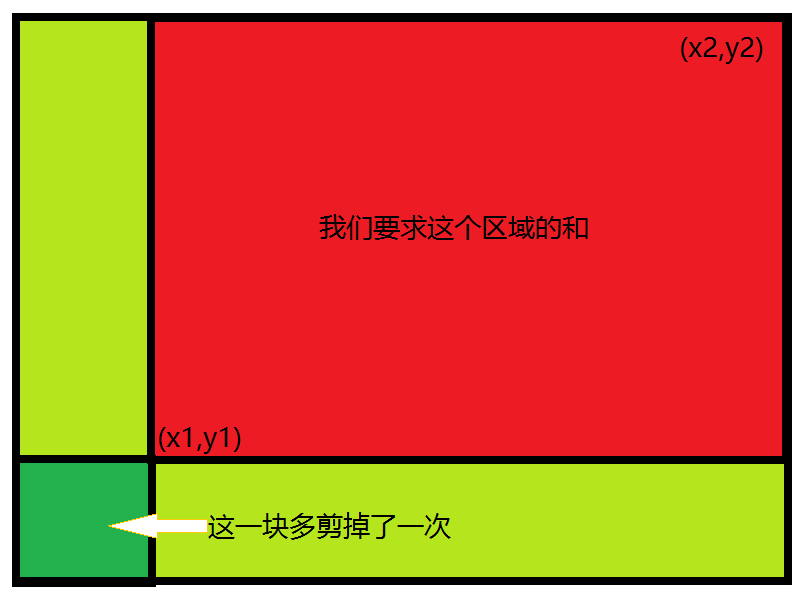
我们对[L,R]区间进行加value操作，在C[L]处加上value，在C[R+1]处减去value
最后求序列的每个位置变成了多少，只要看一下这个位置上C的前缀和就可以

升级版：对于一个n*m的表格，要求支持操作ADD(x1,y1,x2,y2,a)，表示对于以(x1,y1)为左下角，(x2,y2)为右上角的矩形区域，每个元素都加上a。问最后的表格的样子
和一维版的做法类似。
用数组C存修改信息。在C[x1][y1]处加上a，在C[x2+1][y1]和C[x1][y2+1]处减a，在C[x2+1][y2+1]再加上a。
最后(i,k)位置上的数值就是C数组在(i,k)位置的前缀和。
树状数组区间修改单点查询的时候要用！

 

上述知识点为我在网上dalao博主找的较好的解释！

 

我自己对用差分对区间操作的理解，我们对[L,R]区间进行加value操作，在C[L]处加上value，在C[R+1]处减去value，因为最后要用c数组的前缀和与原始数组分别相加，所以在C[L]处加上value只对L以后数有影响，在L以后的前缀和都加上了value，因为要求的作用范围是[L,R]，所以R以后的前缀和不能产生影响，则应该在C[R+1]处减去value，以与前面加的value相抵消。二维数组同理。

下面是我遇到的例题：

上交大OJ 1002：二哥种花生

Description

二哥在自己的后花园里种了一些花生，也快到了收获的时候了。这片花生地是一个长度为L、宽度为W的矩形，每个单位面积上花生产量都是独立的。他想知道，对于某个指定的区域大小，在这么大的矩形区域内，花生的产量最大会是多少。

Input Format

第1行有2个整数，长度L和宽度W。

第2行至第L+1行，每行有W个整数，分别表示对应的单位面积上的花生产量A（ 0≤A<10 ）。

第L+2行有2个整数，分别是指定的区域大小的长度a和宽度b。

Output Format

输出一个整数m，表示在指定大小的区域内，花生最大产量为m。

Sample Input

4 5
1 2 3 4 5
6 7 8 0 0
0 9 2 2 3
3 0 0 0 1
3 3

Sample Output

38

样例解释

左上角：38 = (1+2+3) + (6+7+8) + (0+9+2)

数据范围

对于30%的数据： 1≤L,W≤100；

对于100%的数据： 1≤L,W≤1000。

全部区域大小满足：1≤a≤L，1≤b≤W 。

 

分析：这里就用到前缀和来求解遍历，以防超时！

AC code:

#include <iostream>
using namespace std;
const int maxn = 1000 + 5;
int c[maxn][maxn] = {0};
int main() {
    int L, W;
    cin >> L >> W;
    for(int i = 1; i <= L; i++)
        for(int j = 1; j <= W; j++) {
            cin >> c[i][j];
            c[i][j] = c[i][j] + c[i][j-1] + c[i-1][j] - c[i-1][j-1];      //求前缀和
        }

    int a, b;
    long max=0, sum;
    cin >> a >> b;
    
    for( int i = 1; i <= L - a + 1; i++) {
        for(int j = 1; j <= W - b + 1; j++) {
            sum = c[i+a-1][j+b-1] - c[i-1][j+b-1] - c[i+a-1][j-1] + c[i-1][j-1];
            if(sum > max)
                max = sum;
        }
    }
    cout << max;
    return 0;
}