【算法】二分查找

二分查找，又叫折半查找，是一种在有序数组（以及其它线性存储结构）中查找一个元素的高效算法。时间复杂度为   O(logⁿ)

算法思想

假设数组长度为len，待查找的元素为T。

 

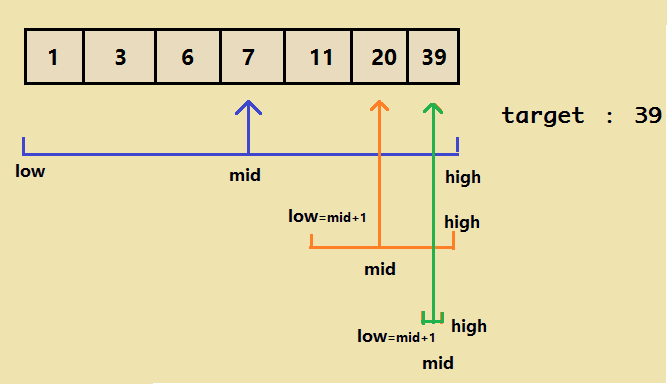
1、让low= 0 ， high  = len-1

2、如果low>high，则查找以失败结束，否则循环进行查找

3、让mid 为  不大于 (Low+High) /2 的整数，即 mid = floor((Low+High)/2)

4、如果arr[mid]<T ,则 让 Low = mid +1,继续第二步

     如果arr[mid]>T 则让High = mid - 1,继续第二步

     如果arr[mid]==T,则查找成功，mid就是T在数组arr中的index，返回mid。

 

 

 

 

注意事项

①使用的前提是数组有序

②如果数组中有重复元素，当需要查找的元素恰好是重复元素时，返回的索引是这些重复元素中哪个的索引值是不确定。这需要注意的。如下查找元素3。

            [1,2,3,3,7]      返回的是第一个3的index

            [1,3,3,7,8]      返回的是最后一个3的index

            [1,3,3,3,7]      返回的是中间一个3的index

 

 

代码实现

public static int binarySearch(int[] arr,int target)
{
        int low = 0;
        int high = arr.length - 1;
        int mid=-1;
        
        while (low <= high)
        {
            mid = (high-low)/2 + low ;    //使用 (low+high) /2 可能会溢出。对于java，使用 mid =  (high+low)>>>1; 也可以防止溢出
            

            if (arr[mid] < target)
                low = mid + 1;
            else if (arr[mid] > target)
                high = mid - 1;
            
            else   //arr[mid] == target
                return mid; //  found
        }
        return -1; // not found.

}

 

对于时间复杂度的分析

为什么时间复杂度最坏为   O(logⁿ)呢？ (注意：计算机科学中， log 默认都是以2为底的)

最坏的情况为：我们去查找数组中的最后一个元素（或者第一个元素），因为他们都最偏离中间,需要不断折半，直到最后折半后的数组只剩下一个元素。

假设这个数组长度为 n   ，且假设 2^x  = n ;那么 让n 递归的除以2，需要x次，才能近视为1。x即为时间需要循环的次数。

x = logⁿ