- 前言:
本学期JAVA第三阶段学习已结束以及本学期JAVA课程已完结,在此,对于第三阶段的学习与作业练习进行总结。在最后一阶段,对javafx进行了学习与了解;PTA作业完成了“点线形系列5-凸五边形的计算”、“电信计费系列1-座机计费”、“电信计费系列2-手机+座机计费”以及收费系列的信息收费处理。难度上,多边形计算系列的题目难度较大,电信收费系列的题目难度降低但是测试点依然细节繁琐。就此,对于各题进行总结与学习以及题目分析。
1)PTA第四次大作业整体上讲,整体难度较大,为两道连续的关于“点线系列的五边形的计算”,题目繁琐复杂。这次题目是所有电线系列题目中最难的也是系列最后一道题目。其题目要求:用户输入一组选项和数据,进行与五边形有关的计算。以下五边形顶点的坐标要求按顺序依次输入,连续输入的两个顶点是相邻顶点,第一个和最后一个输入的顶点相邻。输入五个点坐标时,有两种情况要求判断,一判断是否是五边形,判断结果输出true/false、二判断是凹五边形(false)还是凸五边形(true),如果是凸五边形,则再输出五边形周长、面积,结果之间以一个英文空格符分隔。当输入七个点坐标时,输入七个点坐标,前两个点构成一条直线,后五个点构成一个凸五边形、凸四边形或凸三角形,输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个,再按面积从小到大输出被直线分割成两部分的面积。输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),输出两个多边形公共区域的面积。注:只考虑每个多边形被另一个多边形分割成最多两个部分的情况,不考虑一个多边形将另一个分割成超过两个区域的情况、等情况。可见,题目繁琐复杂,需要利用面向对象将其简化;并且使用合理算法优化程序。
2)PTA大作业六、七、八为电信收费系列,包括“ 电信计费系列1-座机计费”、“电信计费系列2-手机+座机计费”、“ 电信计费系列3-短信计费”。题目难度相对于前面的降低,不过类图丰富复杂,需要花功夫梳理。要求如下:
实现一个简单的电信计费程序:针对南昌市电信分公司针对市内座机用户采用的计费方式进行计算输出。题目要求设定好的输入格式,以固定形式用正则表达式判断。其中时间必须符合"yyyy.MM.dd HH:mm:ss"格式并且使用SimpleDateFormat类更便于编写。随之的一系列的测试点是对 座机打座机、座机打手机、手机打座机、手机打手机、手机给手机发信息的计算与输出。题目看是繁琐,实则仅是类较多,对于算法考察较少,理解之后写起来比较好上手。
- 题目 设计与分析 踩坑心得 改进建议
(1)PTA大作业五 点线形系列5-凸五边形的计算-1
(2)PTA大作业五 点线形系列5-凸五边形的计算-2
设计与分析:
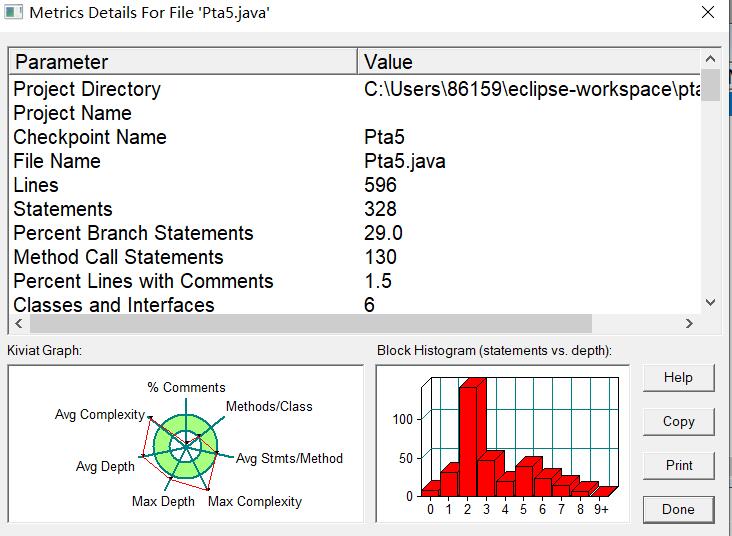
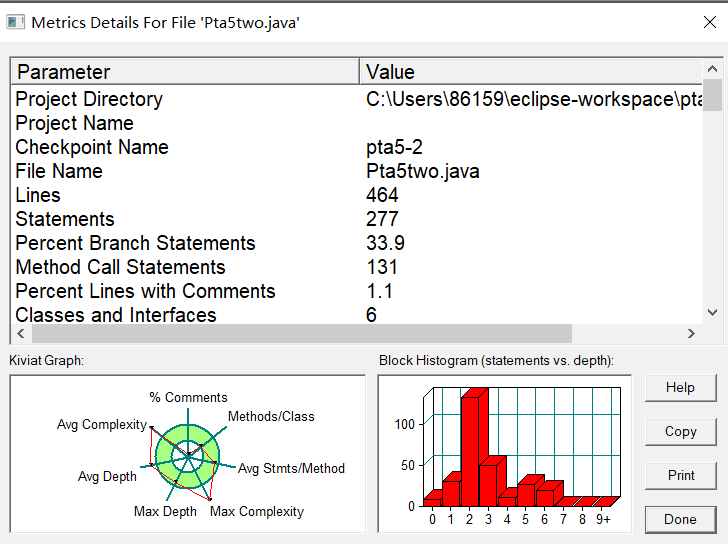
由SourceMonitor图解可以的出,题目较复杂运行过程繁琐。对于这两道题目,其实就是同一题干的两道题目,是多边形点线序列中最难最复杂的一道题目。题目一共需求六个功能:1:输入五个点坐标,判断是否是五边形,判断结果输出true/false。
2:输入五个点坐标,判断是凹五边形(false)还是凸五边形(true),如果是凸五边形,则再输出五边形周长、面积,结果之间以一个英文空格符分隔。 若五个点坐标无法构成五边形,输出"not a pentagon"
3:输入七个点坐标,前两个点构成一条直线,后五个点构成一个凸五边形、凸四边形或凸三角形,输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个,再按面积从小到大输出被直线分割成两部分的面积(不换行)。若直线与多边形形的一条边线重合,输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入,若前两点重合,输出"points coincide"。
4:输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),判断它们两个之间是否存在包含关系(一个多边形有一条或多条边与另一个多边形重合,其他部分都包含在另一个多边形内部,也算包含)。
两者存在六种关系:1、分离(完全无重合点) 2、连接(只有一个点或一条边重合) 3、完全重合 4、被包含(前一个多边形在后一个多边形的内部)5、交错 6、包含(后一个多边形在前一个多边形的内部)。
各种关系的输出格式如下:
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon
5:输入十个点坐标,前、后五个点分别构成一个凸多边形(三角形、四边形、五边形),输出两个多边形公共区域的面积。注:只考虑每个多边形被另一个多边形分割成最多两个部分的情况,不考虑一个多边形将另一个分割成超过两个区域的情况。
6:输入六个点坐标,输出第一个是否在后五个点所构成的多边形(限定为凸多边形,不考虑凹多边形),的内部(若是五边形输出in the pentagon/outof the pentagon,若是四边形输出in the quadrilateral/outof the quadrilateral,若是三角形输出in the triangle/outof the triangle)。输入入错存在冗余点要排除,冗余点的判定方法见选项5。如果点在多边形的某条边上,输出"on the triangle/on the quadrilateral/on the pentagon"。由于题目复杂过高,直接算的方法会很麻烦以及难以实现,可以使用向量积解决很多问题。
踩坑心得:
public boolean isPentagon() { boolean flag = true; if ((p[3] - p[1]) * (p[4] - p[2]) == (p[5] - p[3]) * (p[2] - p[0])) flag = false; else if ((p[7] - p[5]) * (p[4] - p[2]) == (p[5] - p[3]) * (p[6] - p[4])) flag = false; else if ((p[7] - p[5]) * (p[8] - p[6]) == (p[9] - p[7]) * (p[6] - p[4])) flag = false; else if ((p[9] - p[1]) * (p[8] - p[6]) == (p[9] - p[7]) * (p[8] - p[0])) flag = false; else if ((p[9] - p[1]) * (p[2] - p[0]) == (p[3] - p[1]) * (p[8] - p[0])) flag = false; double t1 = Xmul(p[6] - p[0], p[7] - p[1], p[4] - p[0], p[5] - p[1]) * Xmul(p[6] - p[2], p[7] - p[3], p[4] - p[2], p[5] - p[3]); double t2 = Xmul(p[8] - p[2], p[9] - p[3], p[6] - p[2], p[7] - p[3]) * Xmul(p[8] - p[4], p[9] - p[5], p[6] - p[4], p[7] - p[5]); double t3 = Xmul(p[0] - p[4], p[1] - p[5], p[8] - p[4], p[9] - p[5]) * Xmul(p[0] - p[6], p[1] - p[7], p[8] - p[6], p[9] - p[7]); if (t1 < 0 || t2 < 0 || t3 < 0) flag = false; return flag; } public boolean isConvex() { boolean flag = true; double t1 = Xmul(p[2] - p[0], p[3] - p[1], p[8] - p[0], p[9] - p[1]); double t2 = Xmul(p[4] - p[2], p[5] - p[3], p[0] - p[2], p[1] - p[3]); double t3 = Xmul(p[6] - p[4], p[7] - p[5], p[2] - p[4], p[3] - p[5]); double t4 = Xmul(p[8] - p[6], p[9] - p[7], p[4] - p[6], p[5] - p[7]); double t5 = Xmul(p[0] - p[8], p[1] - p[9], p[6] - p[8], p[7] - p[9]); if (t1 < 0 || t2 < 0 || t3 < 0 || t4 < 0 || t5 < 0) flag = false; return flag; } public static double Xmul(double x1, double y1, double x2, double y2) {// 求两向量叉乘 return x1 * y2 - x2 * y1; }
对于此处的计算,由于需要判断多次不相邻边不相交、相邻边相交的情况,利用向量积是很好的办法。对于两个相交的边,其中一条边的两点必定在另一条线的异侧,不相交的边则反之。可以由两次向量积的计算的乘积来判断是否在同侧或是异侧。
public static Point getJpoint(Line line1,Line line2){
double area1=Math.abs( 0.5*Pentagon.Xmul(line2.x1-line1.x1, line2.y1-line1.y1
,line2.x2-line1.x1,line2.y2-line1.y1) );
double area2=Math.abs( 0.5*Pentagon.Xmul(line2.x1-line1.x2, line2.y1-line1.y2
,line2.x2-line1.x2,line2.y2-line1.y2) );
double x=(area1*line1.x2+area2*line1.x1)/(area1+area2);
double y=(area1*line1.y2+area2*line1.y1)/(area1+area2);
Point point = new Point(x,y);
return point;
}
由于题目后期要求求面积,故先写出一个求交点的函数,以简化代码方便使用,对于求交点,还是要巧妙的使用向量积。首先给出用向量积求出线段是否相交的方法:
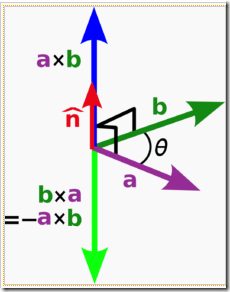
向量外积,也叫向量叉乘。与内积不同的是,向量外积的结果还是一个向量,它的模为两个向量围成的平行四边形的面积,方向与平行四边形所在的平面垂直,指向由右手螺旋定则确定。写成公式为:
∣∣∣a→×b→∣∣∣=∣∣a→∣∣∙∣∣∣b→∣∣∣∙sinθ|a→×b→|=|a→|∙|b→|∙sinθ。 其中,θ为两个向量的夹角。如果知道两个向量的坐标a→=(ax,ay,az)a→=(ax,ay,az)、b→=(bx,by,bz)b→=(bx,by,bz),则两个向量的外积的坐标运算为:
a→×b→=(aybz−azby)i→+(azbx−axbz)j→+(axby−aybx)k→a→×b→=(aybz−azby)i→+(azbx−axbz)j→+(axby−aybx)k→
为了便于记忆,还可以写为三阶行列式的形式: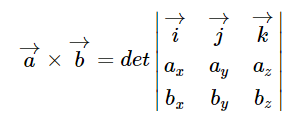 。
。
利用向量积判断点与线的相对位置:假设有向线段为AB−→−AB→,点为CC,首先计算外积AC−→−×AB−→−=(AC−→−x⋅AB−→−y−AC−→−y⋅AB−→−x)k→AC→×AB→=(AC→x⋅AB→y−AC→y⋅AB→x)k→ (因为有AB−→−z=0AB→z=0、AC−→−z=0AC→z=0)。根据右手螺旋定则,如果k→k→的系数为正数,说明点C在线段AB的右侧;如果为负数,说明点C在线段AB的左侧;如果为0,说明点C在线段AB所在的直线上。
改进建议:
对于这类点线类题目,数据较多就会繁琐复杂,建议改进所有算法都使用向量积进行运算,包括线与线的位置,点与线的位置。判断方法总结:1.如果线段CD的两个端点C和D,与另一条线段的一个端点(A或B,只能是其中一个)连成的向量,与向量AB做叉乘,若结果为0,则线段AB与线段CD相交;
2.如果线段CD的两个端点C和D,与另一条线段的一个端点(A或B,只能是其中一个)连成的向量,与向量AB做叉乘,若结果异号,表示C和D分别在直线AB的两边,若结果同号,则表示CD两点都在AB的一边,则肯定不相交。
3.如果线段CD的两端满足在线段AB的两边,同理:还需证明端点A和段点B也在线段CD的两边;
由于三道题目是同一系列题目,在此一起分析与学习。由SourceMonitor图以及类可以看出程序类别复杂多样,但是实际上算法较简单。题目有三题的要求分别为:实现一个简单的电信计费程序:假设南昌市电信分公司针对市内座机用户采用的计费方式:月租20元,接电话免费,市内拨打电话0.1元/分钟,省内长途0.3元/分钟,国内长途拨打0.6元/分钟。不足一分钟按一分钟计。南昌市的区号:0791,江西省内各地市区号包括:0790~0799以及0701。输入信息包括两种类型
1、逐行输入南昌市用户开户的信息,每行一个用户,
格式:u-号码 计费类型 (计费类型包括:0-座机 1-手机实时计费 2-手机A套餐)
例如:u-079186300001 0
座机号码除区号外由是7-8位数字组成。
本题只考虑计费类型0-座机计费,电信系列2、3题会逐步增加计费类型。
2、逐行输入本月某些用户的通讯信息,通讯信息格式:
座机呼叫座机:t-主叫号码 接听号码 起始时间 结束时间
t-079186330022 058686330022 2022.1.3 10:00:25 2022.1.3 10:05:11
以上四项内容之间以一个英文空格分隔,
时间必须符合"yyyy.MM.dd HH:mm:ss"格式。提示:使用SimpleDateFormat类。
以上两类信息,先输入所有开户信息,再输入所有通讯信息,最后一行以“end”结束。
3、针对市内座机用户采用的计费方式(与电信计费系列1内容相同):
月租20元,接电话免费,市内拨打电话0.1元/分钟,省内长途0.3元/分钟,国内长途拨打0.6元/分钟。不足一分钟按一分钟计。
假设本市的区号:0791,江西省内各地市区号包括:0790~0799以及0701。
4、针对手机用户采用实时计费方式:
月租15元,市内省内接电话均免费,市内拨打市内电话0.1元/分钟,市内拨打省内电话0.2元/分钟,市内拨打省外电话0.3元/分钟,省内漫游打电话0.3元/分钟,省外漫游接听0.3元/分钟,省外漫游拨打0.6元/分钟;
5、实现一个简单的电信计费程序,针对手机的短信采用如下计费方式:
1、接收短信免费,发送短信0.1元/条,超过3条0.2元/条,超过5条0.3元/条。
2、如果一次发送短信的字符数量超过10个,按每10个字符一条短信进行计算。
注:被叫电话属于市内、省内还是国内由被叫电话的接听地点区号决定,比如以下案例中,南昌市手机用户13307912264在区号为020的广州接听了电话,主叫号码应被计算为拨打了一个省外长途,同时,手机用户13307912264也要被计算省外接听漫游费:
注意:
本题非法输入只做格式非法的判断,不做内容是否合理的判断(时间除外,否则无法计算),比如:
1、输入的所有通讯信息均认为是同一个月的通讯信息,不做日期是否在同一个月还是多个月的判定,直接将通讯费用累加,因此月租只计算一次。
2、记录中如果同一电话号码的多条通话记录时间出现重合,这种情况也不做判断,直接 计算每条记录的费用并累加。
3、用户区号不为南昌市的区号也作为正常用户处理。
输出格式:
根据输入的详细通讯信息,计算所有已开户的用户的当月费用(精确到小数点后2位,
单位元)。假设每个用户初始余额是100元。
每条通讯信息单独计费后累加,不是将所有时间累计后统一计费。
格式:号码+英文空格符+总的话费+英文空格符+余额
每个用户一行,用户之间按号码字符从小到大排序。
错误处理:
输入数据中出现的不符合格式要求的行一律忽略。
踩坑心得:
String regex1 = "([u])([-])+([0-9]{11,12})+\\s+([0-2]{1})";
Pattern pattern1 = Pattern.compile(regex1);
Matcher matcher1 = pattern1.matcher(a);
String regex2 = "([t])([-])([0-9]{11,12})\\s([0-9]{11,12})\\s([0-9]{4}.([1-9]{1}|1[0-2]).([1-9]{1}|1[0-9]|2[0-9]|3[0-1])\\s(0[0-9]|1[0-9]|2[0-3]):([0-5]{1}[0-9]):([0-5]{1}[0-9]))\\s([0-9]{4}.([1-9]{1}|1[0-2]).([1-9]{1}|1[0-9]|2[0-9]|3[0-1])\\s(0[0-9]|1[0-9]|2[0-3]):([0-5]{1}[0-9]):([0-5]{1}[0-9]))";
Pattern pattern2 = Pattern.compile(regex2);
Matcher matcher2 = pattern2.matcher(a);
第一题Test()函数中代码对输入的识别主要是靠正则表达式来判断与提取,此处正则表达式需要制作细节处理,稍有遗漏测点就会出大问题。对于时间的处理输入必须符合要求,比如不能输入2022.13.61 28:72:65。正则表达式中,matcher.group()的使用也有一些该注意的,matcher.group(0)表示整个被识别的表达式,而matcher.group(1).....之类的以括号分割计数提取括号中的内容。
String regex1 = "([u])([-])+([0-9]{10,12})+\\s+([0-2]{1})";
Pattern pattern1 = Pattern.compile(regex1);
Matcher matcher1 = pattern1.matcher(a);
// 座机打座机
String regex2 = "([t])([-])([0-9]{10,12})\\s([0-9]{10,12})\\s([0-9]{4}.([1-9]{1}|1[0-2]).([1-9]{1}|1[0-9]|2[0-9]|3[0-1])\\s(0[0-9]|1[0-9]|2[0-3]):([0-5]{1}[0-9]):([0-5]{1}[0-9]))\\s([0-9]{4}.([1-9]{1}|1[0-2]).([1-9]{1}|1[0-9]|2[0-9]|3[0-1])\\s(0[0-9]|1[0-9]|2[0-3]):([0-5]{1}[0-9]):([0-5]{1}[0-9]))";
Pattern pattern2 = Pattern.compile(regex2);
Matcher matcher2 = pattern2.matcher(a);
// 座机打手机
String regex3 = "([t])([-])([0-9]{10,12})\\s([0-9]{11})\\s([0-9]{3,4})\\s([0-9]{4}.([1-9]{1}|1[0-2]).([1-9]{1}|1[0-9]|2[0-9]|3[0-1])\\s(0[0-9]|1[0-9]|2[0-3]):([0-5]{1}[0-9]):([0-5]{1}[0-9]))\\s([0-9]{4}.([1-9]{1}|1[0-2]).([1-9]{1}|1[0-9]|2[0-9]|3[0-1])\\s(0[0-9]|1[0-9]|2[0-3]):([0-5]{1}[0-9]):([0-5]{1}[0-9]))";
Pattern pattern3 = Pattern.compile(regex3);
Matcher matcher3 = pattern3.matcher(a);
// 手机打手机
String regex4 = "[t][-]([0-9]{11})\\s([0-9]{3,4})\\s([0-9]{11})\\s([0-9]{3,4})\\s([0-9]{4}.([1-9]{1}|1[0-2]).([1-9]{1}|1[0-9]|2[0-9]|3[0-1])\\s(0[0-9]|1[0-9]|2[0-3]):([0-5]{1}[0-9]):([0-5]{1}[0-9]))\\s([0-9]{4}.([1-9]{1}|1[0-2]).([1-9]{1}|1[0-9]|2[0-9]|3[0-1])\\s(0[0-9]|1[0-9]|2[0-3]):([0-5]{1}[0-9]):([0-5]{1}[0-9]))";
Pattern pattern4 = Pattern.compile(regex4);
Matcher matcher4 = pattern4.matcher(a);
// 手机打座机
String regex5 = "([t])([-])([0-9]{11})\\s([0-9]{3,4})\\s([0-9]{10,12})\\s([0-9]{4}.([1-9]{1}|1[0-2]).([1-9]{1}|1[0-9]|2[0-9]|3[0-1])\\s(0[0-9]|1[0-9]|2[0-3]):([0-5]{1}[0-9]):([0-5]{1}[0-9]))\\s([0-9]{4}.([1-9]{1}|1[0-2]).([1-9]{1}|1[0-9]|2[0-9]|3[0-1])\\s(0[0-9]|1[0-9]|2[0-3]):([0-5]{1}[0-9]):([0-5]{1}[0-9]))";
Pattern pattern5 = Pattern.compile(regex5);
Matcher matcher5 = pattern5.matcher(a);
第二题Test()类中增加了手机,直接增加了好多种情况,对于不同的情况正则表达式的书写大有不同,需要修改,之前以为变化不大没去修改,测试错漏了很多。
String regex1 = "([u])([-])+(1[0-9]{10})+\\s+(3)";
Pattern pattern1 = Pattern.compile(regex1);
Matcher matcher1 = pattern1.matcher(a);
String regex2 = "([m])([-])(1[0-9]{10})\\s(1[0-9]{10})\\s((\\d|\\.|\\s|\\,|[a-zA-Z])+)$";
Pattern pattern2 = Pattern.compile(regex2);
Matcher matcher2 = pattern2.matcher(a);
第三题的主要是对手机与手机的信息处理,与之前对比,简洁了许多。对于信息的正则表达式,由于题目中要求只允许“数字、字母、英文逗号、英文句号和空格的出现”,需要对信息进行限定。正则表达式中"|"表示或者,"+"表示有许多个相同元素,就此可以进行限定。需要注意的是,由于只能出现“数字、字母、英文逗号、英文句号和空格的出现”,需要用$对信息进行终止,否则程序将对前面符合要求而后面跟着不符要求的输入进行1常规处理,不符合题意。
改进建议:
建议在正则表达式的书写更精简一些,比如表达数字[0-9]可以换成\\d的1一系列操作,这样更容易看清楚以及时找出错误。在编译代码的时候不用过于着急,应当顾其全面,经量减少遗漏。
总结:
(1)在第三阶段的学习与作业中,自主学习了向量积求点线、线线之间关系的算法;学习了正则表达式的使用以及其函数的使用;课堂学习了javafx的用法,掌握了javafx的基础操作。
(2)在这几次练习中,逐渐感受到了算法的重要性,可以说算法就是代码的精华部分,没有算法就写不了代码。
(3)感谢OOP课程老师的指导与作业监督,虽然过程很累,但还是得向前看,迎接新的学习。
(4)给老师的建议:建议老师发放题目的时间合理安排,目前课程题目总是集中一个时间发布。我建议将PTA、MOOC以及实验的题目分开时间布置。



