Manacher(马拉车算法)

Manacher(马拉车算法)

P3805 模板manacher 算法

1、写出暴力方法

• 先处理字符串，用#分隔，头为都要有

• 用一个r数组存储每个点的最长子串的半径

• 枚举每个点然后向外扩张

• 扩张完毕后自减 表示半径

• 获取最大值

暴力法如下

string deal(string& str) {
    string temp = "#";
    for (char ch : str)(temp += ch) += '#';
    return temp;
}
int r[22000010] = { 0 };
int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    
    string str;
    cin >> str;
    str = deal(str);
    int len = str.length(), ans = 0, c = 0;
    for (int i = 0; i < len; i++) {
        while (i - r[i] >= 0 && str[i - r[i]] == str[i + r[i]])r[i]++;
        r[i]--;
        ans = max(ans, r[i]);
    }
    return 0;
}

2、通过利用对称性

• 解释：在一个较大的半径范围内 其中的数如果半径较小，那么关于大半径范围对称
• 如图所示

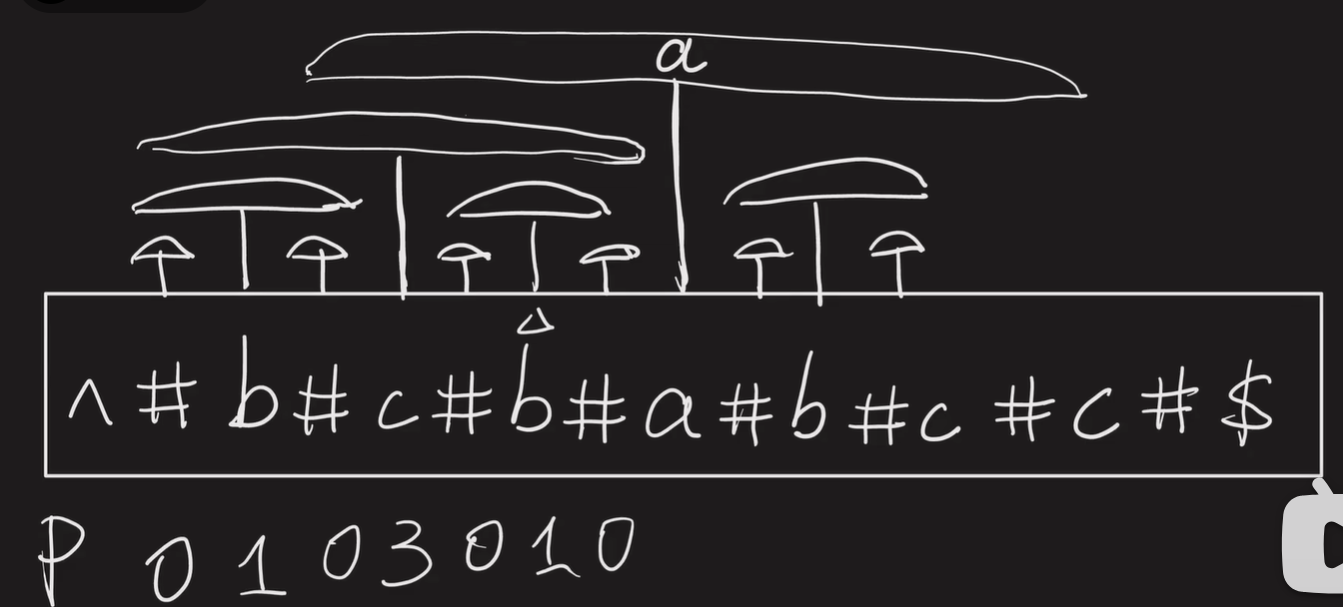
• 用一个变量c记录当前范围最大的并且范围最靠右端的位置
• 每次遇到新的位置时
  • 先将新位置的半径赋为对称的对应半径
    • 如果出现半径超出范围，如图中倒数第二个C，那么赋值为到最右边半径的距离
  • 然后向外拓展判断
  • 最后比较c和当前index的最右端

string deal(string& str) {
    string temp = "#";
    for (char ch : str)(temp += ch) += '#';
    return temp;
}
int r[22000010] = { 0 };
int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    
    string str;
    cin >> str;
    str = deal(str);
    int len = str.length(), ans = 0, c = 0;
    //由于下标0位置为'#'所以直接从下标1开始
    for (int i = 1; i < len; i++) {
        //如果当前点在c的包裹内就赋值，如果刚好在c半径的右边一位，会出现-1
        if (c + r[c] >= i)r[i] = min(r[2 * c - i], c + r[c] - i);
        //暴力法
        while (i - r[i] >= 0 && str[i - r[i]] == str[i + r[i]])r[i]++;
        r[i]--;
        //如果最右端更新，那么c也更新
        if (c + r[c] < i + r[i])c = i;
        ans = max(ans, r[i]);
    }
    cout << ans;
    return 0;
}