浮点数在计算机中的表示

首先看一个 十进制小数11.75 他的二进制表示形式：1011.1100，虽然计算机中数字是以二进制进行存储的，但这种形式的表示是无法在计算机中进行使用的

那么计算机内部是怎么表示小数呢？

根据国际标准IEEE 754 ，任意一个浮点数都可以表示为：

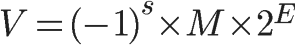
其中:最前面的(-1)^S可以用来表示符号正负；M表示尾数，E为指数；2是基数；

实际上在计算机中的浮点数表示形式是这样的：

对于32位的单精度浮点数， 最高的1位是符号位s，中间8位是指数E，剩下的23位是尾数M

• 指数部分：用EXCESS系统表示。其实也就是我们理解的移码表示。

因为指数可能是负数，需要用正数来表示负数。如8位的单精度浮点数可以表示的范围：00000000~11111111即：0~255。将中间值：01111111（127）表示为0。那么整体可以表示的范围就是-127~128。

• 尾数部分：小数点前面为1。

通过逻辑移位将二进制小数前面变为1，尾数部分只取小数点后面的数。比如二进制浮点数：0.11，移位之后二进制表示：1.1x2^(-1);

例子：

一个单精度二进制浮点数表示为：0-01111110-1000000...0(尾数部分23位)，他所表示的十进制数字是多少？

将其带入浮点数表示公式：

• 第一位0可以表示为正数。

• 中间为指数，它表示的值是01111110（126）-01111111（127）计算得到的，为-1（用EXCESS系统表示）

• 末尾是尾数：加上小数点前面的1，即为1.1

最后二进制表示形式为：1.1x2^(-1),计算可知是0.75

反过来。想要计算单精度浮点数0.75怎么表示为二进制，规则一样：

• 用二进制表示：0.11

• 将小数点前面固定为1后为：1.1x2^(-1)

• -1是EXCESS系统表示的值，实际在二进制中的指数值为：-1+127（01111111）=126（01111110）

关于浮点数表述还可以看这一道例题：https://www.ruanyifeng.com/blog/2010/06/ieee_floating-point_representation.html