1、红黑树的特性
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
(4)如果一个节点是红色的,则它的子节点必须是黑色的。不可以同时存在两个红色节点相连
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
如果一个节点存在黑色子节点,那么该节点肯定有两个子节点
2、插入操作
-
查找插入的位置:插入节点的颜色必须是红色,插入黑色节点会破坏平衡
-
插入后自平衡
红黑树插入情景分析:
(1) 情景1:红黑树为空树
-
将插入节点作为根节点,然后将根节点设置为黑色
(2) 情景2:插入点的key已存在
-
替换原节点的value值
(3) 情景3:插入节点的父节点是黑节点
-
直接插入,不会影响自平衡
(4) 情景4:插入节点的父节点是红节点
根据性质2:父节点为红色一定不是根节点;根据性质4:爷节点肯定是黑色。
情景4.1:叔叔节点存在,且为红色
-
将父节点P和叔节点U改为黑色
-
爷节点PP改为红色。
-
进行后续处理:
-
如果PP的父节点是黑色,则无需处理
-
如果PP的父节点是红色,将PP设为当前插入节点,继续做自平衡处理
情景4.2:叔节点不存在或为黑节点,且插入节点的父节点是爷节点的左孩子
注意:叔叔节点应该非红即空,否则破坏性质5
情景4.2.1:插入节点是父节点的左孩子(LL双红情况)
-
将父节点P设为黑色,将爷节点PP设为红色
-
对爷节点PP进行右旋
情景4.2.1:插入节点是父节点的右孩子(LR双红情况)
-
对父节点P进行左旋
-
将P设为当前节点,得到LL双红情况
-
将I设为黑色,将爷节点PP设为红色
-
对爷节点PP进行右旋
情景4.3:叔叔节点不存在或为黑节点,且插入节点的父节点是爷节点的右孩子
对应情景4.2,只是方向相反
情景4.3.1:插入节点是父节点的右孩子(RR双红情况)
-
父节点P设为黑色,爷节点PP设为红色
-
对爷节点PP进行左旋
情景4.3.2:插入节点是父节点的左孩子(LR双红)
-
对父节点p进行右旋
-
将P节点作为当前节点,得到RR双红情况
-
把I设为黑色,爷节点PP设为红色
-
对爷节点PP进行左旋
示例
3、从2-3树到红黑树
红黑树的起源,自然是二叉查找树了,这种树结构从根节点开始,左子节点小于它,右子节点大于它。每个节点都符合这个特性,所以易于查找,是一种很好的数据结构。但是它有一个问题,就是容易偏向某一侧,这样就像一个链表结构了,失去了树结构的优点,查找时间会变坏。红黑树就是一种平衡树,它可以保证二叉树基本符合矮矮胖胖的结构,但是理解红黑树之前,必须先了解另一种树,叫2-3树,红黑树背后的逻辑就是它。
(1) 2-3树的组成
一颗2-3树或为一颗空树,或有以下节点组成:
-
2-节点,含有一个元素和两个子树(左右子树),左子树所有元素的值均小于它父节点,右子树所有元素的值均大于它父节点;
-
3-节点,还有两个元素和三个子树(左中右子树),左子树所有元素的值均小于它父节点,中子树所有元素的值都位于父节点两个元素之间,右子树所有元素的值均大于它父节点;
-
子树可以是空树、2-节点或者3-节点;
-
没有元素相等的节点。
(2) 2-3树的插入
1.向2-节点中插入元素;
直接插入
2.一颗棵只含有一个节点且为3-节点的树中插入元素
3.向一个父节点为2-节点的3-节点中插入元素
如果命中查找结束于3-节点,先临时将其成为4-节点,把待插入元素添加到其中,然后将4-节点转化为3个2-节点,中间的节点成为左右节点的父节点。如果之前临时4-节点有父节点,就会变成向一个父节点为2-节点的3-节点中插入元素,中间节点与父节点为2-节点的合并。
4.向一个父节点为3-节点的3-节点中插入元素。
插入元素后一直向上分解临时的4-节点,直到遇到2-节点的父节点变成3-节点不再分解。如果达到树根节点还是4-节点,则进行分解根节点,此时树高+1(只有分解根节点才会增加树高)。
(3) 2-3树与红黑树
红黑树的背后逻辑就是2-3树的逻辑,但是由于用红黑作为标记这个小技巧,最后实现的代码量并不大。(但是,要直接理解这些代码是如何工作的以及背后的道理,就比较困难了。所以你一定要理解它的演化过程,才能真正的理解红黑树)
我们来看看红黑树和2-3树的关联,首先,最台面上的问题,红和黑的含义。红黑树中,所有的节点都是标准的2-节点,为了体现出3-节点,这里将3-节点的两个元素用左斜红色的链接连接起来,即连接了两个2-节点来表示一个3-节点。这里红色节点标记就代表指向其的链接是红链接,黑色标记的节点就是普通的节点。所以才会有那样一条定义,叫“从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点”,因为红色节点是可以与其父节点合并为一个3-节点的,红黑树实现的其实是一个完美的黑色平衡,如果你将红黑树中所有的红色链接放平,那么它所有的叶子节点到根节点的距离都是相同的。所以它并不是一个严格的平衡二叉树,但是它的综合性能已经很优秀了。
红链接放平:
所以,红黑树的另一种定义是满足下列条件的二叉查找树:
-
红链接均为左链接。
-
没有任何一个结点同时和两条红链接相连。(这样会出现4-节点)
-
该树是完美黑色平衡的,即任意空链接到根结点的路径上的黑链接数量相同。
4、B-树与B+树
B 树是一种平衡的多路查找树,2-3 树和 2-3-4 树都是 B 树的特例,结点所拥有的最大孩子树称为 B 树的阶,因此,2-3 树是 3 阶 B 树,2-3-4 树是 4 阶 B 树。
一个 m 阶的 B 树具有如下属性:
- 如果根结点不是叶结点,则至少有两颗子树
- 每一个非根的分支结点都有 k-1 个元素和 k 个孩子
- 所有叶子结点都处于同一层次
- 值位于 k-1 和 k 之间的子结点,都位于 k-1 和 k 对应的 value 之间
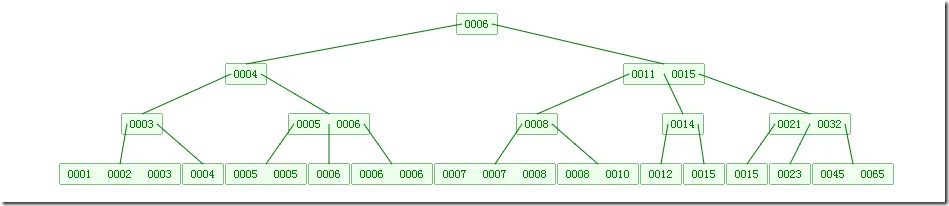
B 树的插入和删除和 2-3 树或 2-3-4 树是类似的,只不过阶数可能会很大而已。B 树可以帮助我们减少内存与外存之间数据的频繁交换,假设一颗 B 树的阶是 1001,高度为 2,它可以存储超过 10 亿个关键字。我们只要让根结点持久保留在内存中,那么寻找一个关键字至多只需要两次硬盘的读取。而如果使用二叉树,那就不得了了,光是树的高度就不知道比使用 B 大到哪里去,对硬盘的读取次数自然也多得多。
B 树还是有缺陷的,如果我们要遍历一颗 B 树,必须往返于每个结点之间,也就意味着得多次访问硬盘,有没有可能让遍历时每个元素只访问一次呢?我们在原有的 B 树结构基础上,加上新的元素组织形式,这就是 B+ 树。
B+ 树与 B 树的差异在于:
- B+ 树的分支结点不保存关键字,只进行数据索引,结点中仅含有其子树中的最大(或最小)关键字
- B+ 树所有的叶子结点包含全部关键字信息,及指向含这些关键字记录的指针,叶子结点本身依关键字的大小从小到大顺序链接
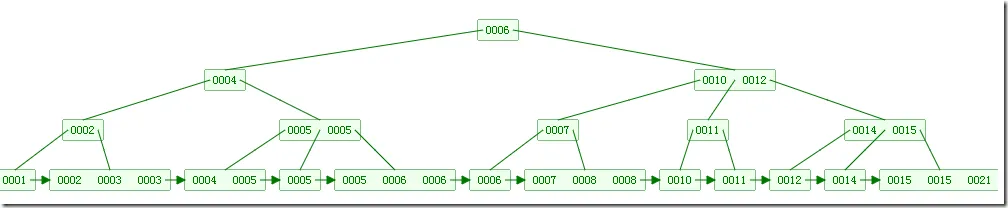
B+ 所有关键字数据地址都存在叶子节点上,所以每次查找的次数都相同,查询效率也比 B 树稳定。B+ 树也结点遍历速度更快,因为只需要从最左侧的叶子结点出发,一直沿着指向下一叶子结点的指针遍历即可。另外,B+ 树天然具备排序功能,因此特别适合带有范围的查找。
本文参考了:https://zhuanlan.zhihu.com/p/104031183
多路查找树(2-3 树、2-3-4 树、B 树、B+ 树) - 低吟不作语 - 博客园 (cnblogs.com)



