奥赛-欧几里得算法-最大公约数
Greatest Common Divisor(GCD)
欧几里得算法据说是最早的算法,用于计算最大公约数,也是数论的基础算法之一。
1.欧几里德算法的思想:
欧几里德算法的思想基于辗转相除法的原理,辗转相除法是欧几里德算法的核心思想,欧几里德算法说白了其实就是辗转相除法的计算机算法的实现而已。下面我们先说说辗转相除法,辗转相除法的内容:如果用gcd(a,b)来表示a和b的最大公约数,那么根据辗转相除法的原理,有gcd(a,b)=gcd(b,a mod (b)),其中mod()表示模运算,并且不妨让a>b,这样方便于模运算。
2.优点
通过模运算的余数是最大公约数之间存在的整数倍的关系,来给比较大的数字进行降维,方便手算;同时,也避免了在可行区间内进行全局的最大公约数的判断测试,只需要选取其余数进行相应的计算就可以直接得到最大公约数,大大提高了运算效率。
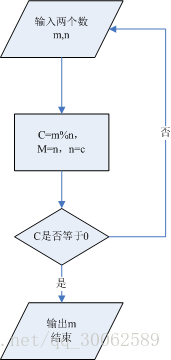
3.过程
4、程序代码
#define ll long long
ll gcd(ll a, ll b) { return !b ? a : gcd(b, a%b); }
这个算法,一定要记住,他很重要。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号