经验集合

2020-08-06

搜索与动态规划有一个共同特点，它要覆盖所有情况。其中记忆化搜索与动规又有同样的特点，在覆盖所有情况的同时有大量的重复计算。

在设计状态时（不论搜索还是动规）要保证覆盖所有状态（动规还要保证有重复）

2020-08-07

拓扑排序给出了动态规划的求解顺序，被取出的点是已知的，没有被取出的点就是未知的。

可以考虑将背包等动态规划题目进行图论建模，并加以拓扑排序深化理解。

记忆化搜索建出的图的逆向拓扑排序才是动规顺序

 

说到「去掉」，试着理解为「留下」。

正着思考难以解决的，可以逆向思维。

2020-08-08

搜索除了状态要覆盖所有的情况，在真实的运行时也要保证不会遗漏

https://www.cnblogs.com/lujin49/p/13453437.html

这个就是个典型例子

2020-08-09

DP与记忆化搜索有着相似性

这种相似性同样体现在代码实现上。

2020-08-11

对于一些有着重复使用的值，预处理是比较好的选择。

https://www.cnblogs.com/lujin49/p/13444234.html是一个例子

2020-08-16

DP能做的DFS不一定能做

考虑区间DP，由于枚举成分，DFS规模会过大

https://www.cnblogs.com/lujin49/p/13511611.html是个例子

2020-08-22

所有的动规，都必须要满足“利用之前的信息”这个条件以达到目的

至于如何利用视题目而定

有些情况下会有特判，有特殊答案

但是只要是能够利用之前的信息，就是动规

2020-08-26

动规、搜索等题目，其转移方法都暗含在题面中

要学会抽丝剥茧剥离出必要信息

2020-08-27

统计颜色种类

本质是各种颜色东西的个数

先加sum=1则color_cnt+1

先减sum==0则color_cnt-1

2020-10-03

利用位运算去掉末尾1的方法

n=n&(n-1)

C(m,n)=A(m,n)/A(m,m)

位运算一定要加括号

保证不重不漏的方法就是按字典序遍历（适用于规模小的情况）

 

 

 

 

 

 

 

 

 

 

 

 二项式定理应该是：

 

 

 

 

 

 

 

 

 

 

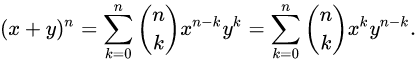
 关于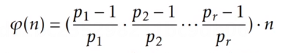的现实意义

 

以30为例

30=2*3*5

2在30的所有系数中每2个去掉一个

3是每3个一个

5是每5个一个

于是剩下的分别是1，2，4

于是有1/2，2/3，4/5

 

 

 

 

 

 

 

 

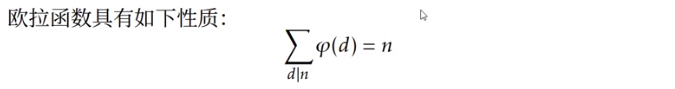
 注意，在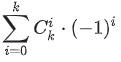中，其意义为：选出i个系数，其指数为1

(-1)ⁱ就是莫比乌斯函数

由于莫比乌斯函数自身的性质，系数为1以上是没有意义的。

附上：