【学习笔记】前馈神经网络（ANN）

前言

最近跟着《神经网络与深度学习》把机器学习的内容简单回顾了一遍，并进行了一定的查缺补漏，比如SVM的一些理解，one-hot向量，softmax回归等等。
然后我将继续跟着这本书，开始学习深度学习的内容。

前馈神经网络

人工神经网络是指一系列受生物学和神经科学启发的数学模型。这些模型主要是通过对人脑的神经元网络进行抽象，构造人工神经元，并按照一定拓扑结构来建立人工神经元之间的连接，来模拟生物神经网络。
早期的神经网络是一种主要的连接主义模型。20世纪80年代中后期，最流行的是分布式并行处理，主要特性是：1）信息表是是分布式的（非局部的）；2）记忆和知识是存储在单元之间的连接上；3）通过逐渐改变单元之间的连接强度来学习新知识
连接主义的神经网络有许多网络结构以及学习方法，虽然早期模型强调模型的生物学合理性，但后期更加关注对某种特性认知能力的模拟。尤其在引入误差反向传播来改进学习能力后，神经网络也越来越多的应用在各种机器学习任务上。
本章主要关注采用误差反向传播来进行学习的神经网络，及作为一种机器学习模型的神经网络。从机器学习的角度看，神经网络模型而可以看作一个非线性模型，其基本组成单元为具有非线性激活函数的神经元，通过大量神经元之间的连接，使得神经网络成为一种高度的非线性的模型，神经元之间的连接的权重就是需要学习的参数，可以在机器学习的框架下通过梯度下降方法来进行学习

• 线性”与“非线性”是数学上的叫法。线性，指的就是两个变量之间成正比例的关系，在平面直角坐标系中表现出来，就是一条直线；而非线性指的就是两个变量之间不成正比，在直角坐标系中是曲线而非直线，例如一元二次方程的抛物线、对数函数等等关系。

神经元

人工神经元简称神经元，是构成神经网络的基本单元，其主要是模拟生物神经元的结构和特性，接受一组信号并产生输出。
假设一个神经元接受了一组输入后，这些输入又会分别各自做出加权和偏置操作，最后得出一个值称之为净输入，这时我们的净输入需要经过一个非线性函数f(·)后，得到神经元的活性值a,其中的非线性函数称为激活函数。

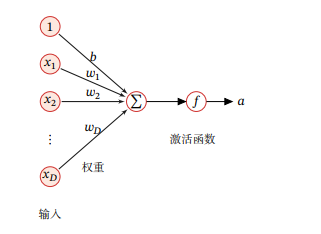
激活函数 激活函数在神经元中非常重要，为了增强网络的表示能力和学习能力，激活函数需要具备以下几个性质：

• 连续并可导（允许少数点上不可导）的非线性函数，可导的激活函数可以直接利用数值优化的方法来学习网络参数
• 激活函数及其导函数要尽可能的简单，有利提高网络计算效率
• 激活函数的导函数的值域要在一个合适的区间内，不能太大也不能太小，否则会影响训练的效率和稳定性

Sigmoid型函数

• Logistic函数
  Logistic函数在逻辑斯蒂回归博文中有介绍 https://www.cnblogs.com/lugendary/p/16023648.html
• Tanh函数
  Tanh函数可以看作放大并平移的Logistic函数，值域为（-1，1）
  
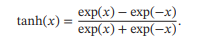
• Hard-Logistic函数和Hard-Tanh函数
  Logistic函数和Tanh函数都是Sigmoid型函数，具有饱和性，但是计算开销较大，因为两个函数都是在0附近接近线性，两端饱和，所以这两个函数可以通过分段函数来近似，也
  就是Hard-Logistic函数和Hard-Tanh函数
  

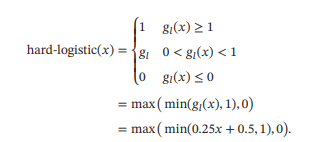
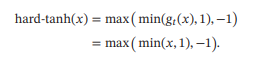
ReLU函数

ReLU函数（Rectified Linear Unit,修正线性单元），也叫Rectifier函数，是目前深度神经网络中经常使用的激活函数，ReLU实际上是一个斜坡函数，定义为：

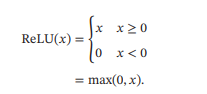
从上图不难看出，ReLU函数其实是分段线性函数，把所有的负值都变为0，而正值不变，这种操作被成为单侧抑制。可别小看这个简单的操作，正因为有了这单侧抑制，才使得神经网络中的神经元也具有了稀疏激活性。尤其体现在深度神经网络模型(如CNN)中，当模型增加N层之后，理论上ReLU神经元的激活率将降低2的N次方倍。这里或许有童鞋会问：ReLU的函数图像为什么一定要长这样？反过来，或者朝下延伸行不行？其实还不一定要长这样。只要能起到单侧抑制的作用，无论是镜面翻转还是180度翻转，最终神经元的输出也只是相当于加上了一个常数项系数，并不影响模型的训练结果。之所以这样定，或许是为了契合生物学角度，便于我们理解吧。
那么问题来了：这种稀疏性有何作用？换句话说，我们为什么需要让神经元稀疏？不妨举栗子来说明。当看名侦探柯南的时候，我们可以根据故事情节进行思考和推理，这时用到的是我们的大脑左半球；而当看蒙面唱将时，我们可以跟着歌手一起哼唱，这时用到的则是我们的右半球。左半球侧重理性思维，而右半球侧重感性思维。也就是说，当我们在进行运算或者欣赏时，都会有一部分神经元处于激活或是抑制状态，可以说是各司其职。再比如，生病了去医院看病，检查报告里面上百项指标，但跟病情相关的通常只有那么几个。与之类似，当训练一个深度分类模型的时候，和目标相关的特征往往也就那么几个，因此通过ReLU实现稀疏后的模型能够更好地挖掘相关特征，拟合训练数据。
此外，相比于其它激活函数来说，ReLU有以下优势：对于线性函数而言，ReLU的表达能力更强，尤其体现在深度网络中；而对于非线性函数而言，ReLU由于非负区间的梯度为常数，因此不存在梯度消失问题(Vanishing Gradient Problem)，使得模型的收敛速度维持在一个稳定状态。这里稍微描述一下什么是梯度消失问题：当梯度小于1时，预测值与真实值之间的误差每传播一层会衰减一次，如果在深层模型中使用sigmoid作为激活函数，这种现象尤为明显，将导致模型收敛停滞不前
优点：采用ReLU的神经元只需要进行加、乘和比较的操作，计算上更加高效．ReLU 函数也被认为具有生物学合理性（Biological Plausibility），比如单侧抑制、宽兴奋边界（即兴奋程度可以非常高）．在生物神经网络中，同时处于兴奋状态的神经元非常稀疏．人脑中在同一时刻大概只有 1% ∼ 4% 的神经元处于活跃状态．Sigmoid 型激活函数会导致一个非稀疏的神经网络，而 ReLU 却具有很好的稀疏性，大约50%的神经元会处于激活状态．在优化方面，相比于Sigmoid型函数的两端饱和，ReLU函数为左饱和函数，且在 𝑥 > 0 时导数为1，在一定程度上缓解了神经网络的梯度消失问题，加速梯度下降的收敛速度．
缺点：ReLU函数的输出是非零中心化的，给后一层的神经网络引入偏置偏移，会影响梯度下降的效率．此外，ReLU神经元在训练时比较容易“死亡”．在训练时，如果参数在一次不恰当的更新后，第一个隐藏层中的某个ReLU神经元在所有的训练数据上都不能被激活，那么这个神经元自身参数的梯度永远都会是0，在以后的训练过程中永远不能被激活．这种现象称为死亡ReLU问题，并且也有可能会发生在其他隐藏层．在实际使用中，为了避免上述情况，有几种ReLU的变种也会被广泛使用．

• 带泄露的ReLU
  带泄露的ReLU（Leaky ReLU）在输入𝑥 < 0时，保持一个很小的梯度𝛾．这样当神经元非激活时也能有一个非零的梯度可以更新参数，避免永远不能被激活
  
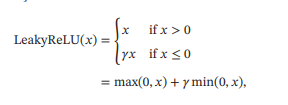
• 带参数的ReLU
  带参数的 ReLU（Parametric ReLU，PReLU）引入一个可学习的参数，不同神经元可以有不同的参数。对于第 𝑖 个神经元，其 PReLU 的定义为
  
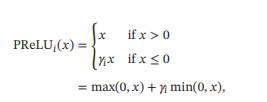
  其中 𝛾𝑖 为 𝑥 ≤ 0 时函数的斜率．因此，PReLU 是非饱和函数．如果 𝛾𝑖 = 0，那么PReLU就退化为ReLU．如果𝛾𝑖 为一个很小的常数，则PReLU可以看作带泄露的ReLU．PReLU 可以允许不同神经元具有不同的参数，也可以一组神经元共享一个参数．
• ELU函数
  ELU（Exponential Linear Unit，指数线性单元）是一个近似的零中心化的非线性函数，其定义为
  
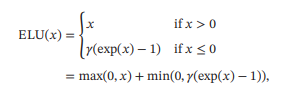
  其中𝛾 ≥ 0是一个超参数，决定𝑥≤0时的饱和曲线，并调整输出均值在0附近．
• Softplus函数
  Softplus 函数可以看作 Rectifier 函数的平滑版本，其定义为
  
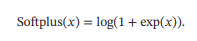
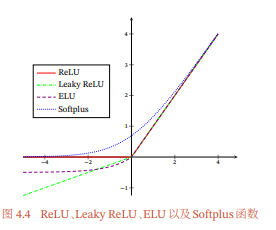
  Softplus函数其导数刚好是Logistic函数．Softplus函数虽然也具有单侧抑制、宽兴奋边界的特性，却没有稀疏激活性．
• ReLU各个函数的图像
  给出了ReLU、Leaky ReLU、ELU以及Softplus函数的示例。
  

Swish函数

Swish 函数是一种自门控（Self-Gated）激活函数，定义为

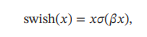
其中 𝜎(⋅) 为 Logistic 函数，𝛽 为可学习的参数或一个固定超参数．𝜎(⋅) ∈ (0, 1) 可以看作一种软性的门控机制．当𝜎(𝛽𝑥)接近于1时，门处于“开”状态，激活函数的输出近似于𝑥 本身；当𝜎(𝛽𝑥)接近于0时，门的状态为“关”，激活函数的输出近似于0．

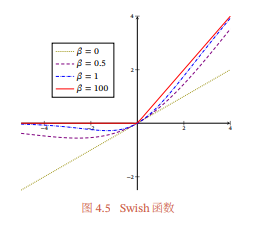
当𝛽 = 0时，Swish函数变成线性函数𝑥/2．当𝛽 = 1时，Swish函数在𝑥 > 0时近似线性，在 𝑥 < 0 时近似饱和，同时具有一定的非单调性．当 𝛽 → +∞ 时，𝜎(𝛽𝑥)趋向于离散的0-1函数，Swish函数近似为ReLU函数．因此，Swish函数可以看作线性函数和ReLU函数之间的非线性插值函数，其程度由参数𝛽控制．

GELU函数

GELU（Gaussian Error Linear Unit，高斯误差线性单元）也是一种通过门控机制来调整其输出值的激活函数，和Swish函数比较类似．其中𝑃(𝑋 ≤ 𝑥)是高斯分布𝒩(𝜇,𝜎2)的累积分布函数，其中𝜇,𝜎为超参数，一般设𝜇=0,𝜎=1即可．由于高斯分布的累积分布函数为S型函数，因此GELU函数可以用Tanh函数或Logistic函数来近似，当使用Logistic函数来近似时，GELU相当于一种特殊的Swish函数．

Maxout单元

Maxout 单元也是一种分段线性函数．Sigmoid型函数、ReLU等激活函数的输入是神经元的净输入𝑧，是一个标量．而 Maxout 单元的输入是上一层神经元的全部原始输出，是一个向量𝒙=[𝑥1;𝑥2;⋯;𝑥𝐷]．每个Maxout单元有𝐾个权重向量𝒘𝑘∈ℝ𝐷和偏置𝑏𝑘(1 ≤ 𝑘 ≤ 𝐾)．对于输入𝒙，可以得到𝐾个净输入𝑧𝑘, 1≤𝑘≤𝐾．
Maxout单元不单是净输入到输出之间的非线性映射，而是整体学习输入到输出之间的非线性映射关系．采用 Maxout 单元的神经网络也叫作Maxout网络．Maxout激活函数可以看作任意凸函数的分段线性近似，并且在有限的点上是不可微的．

网络结构

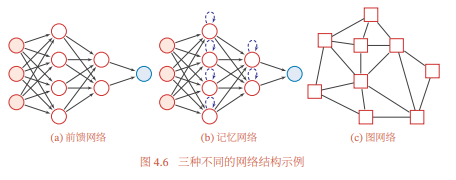
通过一定的连接方式或信息传递方式进行协作的神经元可以看作一个网络，就是神经网络．到目前为止，研究者已经发明了各种各样的神经网络结构．目前常用的神经网络结构有以下三种：

前馈网络

前馈网络中各个神经元按接收信息的先后分为不同的组．每一组可以看作一个神经层．每一层中的神经元接收前一层神经元的输出，并输出到下一层神经元．整个网络中的信息是朝一个方向传播，没有反向的信息传播，可以用一个有向无环路图表示．前馈网络包括全连接前馈网络和卷积神经网络等．前馈网络可以看作一个函数，通过简单非线性函数的多次复合，实现输入空间到输出空间的复杂映射．这种网络结构简单，易于实现．

记忆网络

记忆网络，也称为反馈网络，网络中的神经元不但可以接收其他神经元的信息，也可以接收自己的历史信息．和前馈网络相比，记忆网络中的神经元具有记忆功能，在不同的时刻具有不同的状态．记忆神经网络中的信息传播可以是单向或双向传递，因此可用一个有向循环图或无向图来表示．记忆网络包括循环神经网络、Hopfield 网络、玻尔兹曼机、受限玻尔兹曼机等．记忆网络可以看作一个程序，具有更强的计算和记忆能力．为了增强记忆网络的记忆容量，可以引入外部记忆单元和读写机制，用来保存一些网络的中间状态，称为记忆增强神经网络（Memory Augmented NeuralNetwork，MANN），比如神经图灵机和记忆网络等．

图网络

前馈网络和记忆网络的输入都可以表示为向量或向量序列．但实际应用中很多数据是图结构的数据，比如知识图谱、社交网络、分子（Molecular ）网络等．前馈网络和记忆网络很难处理图结构的数据．图网络是定义在图结构数据上的神经网络（第6.8节）．图中每个节点都由一个或一组神经元构成．节点之间的连接可以是有向的，也可以是无向的．每个节点可以收到来自相邻节点或自身的信息．图网络是前馈网络和记忆网络的泛化，包含很多不同的实现方式，比如 图卷积网络（Graph Convolutional Network，GCN）[Kipf et al., 2016]、图注意力网络（Graph Attention Network，GAT）、消息传递神经网络（Message Passing Neural Network，MPNN）等．
图给出了前馈网络、记忆网络和图网络的网络结构示例，其中圆形节点表示一个神经元，方形节点表示一组神经元．

前馈神经网络

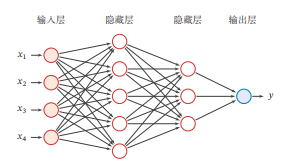
在前馈神经网络中，各神经元分别属于不同的层．每一层的神经元可以接收前一层神经元的信号，并产生信号输出到下一层．第0层称为输入层，最后一层称为输出层，其他中间层称为隐藏层．整个网络中无反馈，信号从输入层向输出层单向传播，可用一个有向无环图表示．

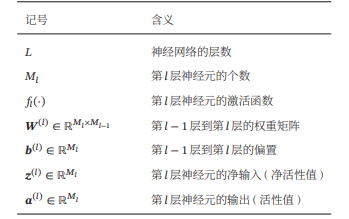
描述前馈神经网络的记号

令𝒂(0) = 𝒙，前馈神经网络通过不断迭代下面公式进行信息传播：

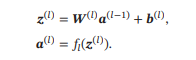
首先根据第𝑙−1层神经元的活性值（Activation）𝒂(𝑙−1) 计算出第𝑙层神经元的净活性值（Net Activation）𝒛(𝑙)，然后经过一个激活函数得到第 𝑙 层神经元的活性值．因此，我们也可以把每个神经层看作一个仿射变换（Affine Transformation）和一个非线性变换．
这样，前馈神经网络可以通过逐层的信息传递，得到网络最后的输出 𝒂(𝐿)．整个网络可以看作一个复合函数𝜙(𝒙;𝑾, 𝒃)，将向量𝒙作为第1层的输入𝒂(0)，将第𝐿层的输出𝒂(𝐿) 作为整个函数的输出．

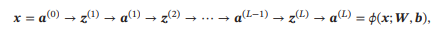
通用近似定理

通用近似定理指的是：如果一个前馈神经网络具有线性输出层和至少一层隐藏层，只要给予网络足够数量的神经元，便可以实现以足够高精度来逼近任意一个在 ℝn 的紧子集 (Compact subset) 上的连续函数。
所谓“挤压”性质的函数是指像 Sigmoid函数的有界函数，但神经网络的通用近似性质也被证明对于其他类型的激活函 数，比如ReLU也都是适用的．
通用近似定理只是说明了神经网络的计算能力可以去近似一个给定的连续函数，但并没有给出如何找到这样一个网络，以及是否是最优的．此外，当应用到机器学习时，真实的映射函数并不知道，一般是通过经验风险最小化和正则化来进行参数学习．因为神经网络的强大能力，反而容易在训练集上过拟合

应用到机器学习

多层前馈神经网络也可以看成是一种特征转换方法，其输出𝜙(𝒙)作为分类器的输入进行分类．特别地，如果分类器𝑔(⋅)为Logistic回归分类器或Softmax回归分类器，那么𝑔(⋅)也可以看成是网络的最后一层，即神经网络直接输出不同类别的条件概率𝑝(𝑦|𝒙)．

• 对于二分类问题𝑦∈{0,1}，并采用Logistic回归，那么 Logistic 回归分类器可以看成神经网络的最后一层．也就是说，网络的最后一层只用一个神经元，并且其激活函数为Logistic函数．网络的输出可以直接作为类别𝑦=1的条件概率，
• 对于多分类问题𝑦∈{1,⋯,𝐶}，如果使用Softmax回归分类器，相当于网络最后一层设置𝐶个神经元，其激活函数为Softmax函数．网络最后一层（第𝐿层）的输出可以作为每个类的条件概率

参数学习

给定训练集为𝒟 = {(𝒙(𝑛), 𝑦(𝑛))}𝑁𝑛=1，将每个样本𝒙(𝑛) 输入给前馈神经网络，得到网络输出为𝒚̂(𝑛)，其在数据集𝒟 上的结构化风险函数为

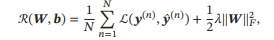
有了学习准则和训练样本，网络参数可以通过梯度下降法来进行学习．在梯度下降方法的每次迭代中，第𝑙 层的参数𝑾(𝑙) 和𝒃(𝑙) 参数更新方式为

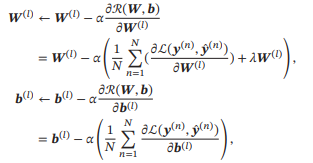
其中𝛼为学习率．
梯度下降法需要计算损失函数对参数的偏导数，如果通过链式法则逐一对每个参数进行求偏导比较低效．在神经网络的训练中经常使用反向传播算法来高效地计算梯度．

反向传播算法

前面的神经网络，就是用很多个感知机（这样算起来比较快）组成一组神经元，不同的神经元组组合在一起就形成了神经网络，我们把训练数据带入，不断的对我们的初始参数进行优化，就是学习过程，这里的训练参数w和b，w代表权重，b代表偏差，偏差可以调整激活阈值。而调整参数的方法就是梯度下降。
反向传播的本质就是我们前馈方法传播一轮后，到最后的输出项的准确率相对于我们的计算复杂程度性价比没有那么高，所以我们要尽可能的榨干我们手上所拥有的数据价值，所以第一轮传播完，还要根据真实值，把第一轮调整好的结果和真实值再做一个损失函数，对这个损失函数进行梯度下降，反过来从最后一层再调整一波一直到第一层的参数（当然也是利用梯度下降），这种方法就是反向传播，这里我要感谢一下这个视频，讲的太好了，通俗易懂，清晰明了，之前看过他的线代的本质没想到还涉足了神经网络，活菩萨啊属于是： https://www.bilibili.com/video/BV16x411V7Qg?spm_id_from=333.337.search-card.all.click
下面给出书中更为详实（但理解起来不太友好的解释）
反向传播算法的含义是：第 𝑙 层的一个神经元的误差项（或敏感性）是所有与该神经元相连的第 𝑙 + 1 层的神经元的误差项的权重和．然后，再乘上该神经元激活函数的梯度,因此，使用误差反向传播算法的前馈神经网络训练过程可以分为以下三步：

• 前馈计算每一层的净输入𝒛(𝑙) 和激活值𝒂(𝑙)，直到最后一层；
• 反向传播计算每一层的误差项𝛿(𝑙)；
• 计算每一层参数的偏导数，并更新参数．
  下面给出使用反向传播算法的随机梯度下降训练过程
  

自动梯度计算

神经网络的参数主要通过梯度下降来进行优化．当确定了风险函数以及网络结构后，我们就可以手动用链式法则来计算风险函数对每个参数的梯度，并用代码进行实现．但是手动求导并转换为计算机程序的过程非常琐碎并容易出错，导致实现神经网络变得十分低效．实际上，参数的梯度可以让计算机来自动计算．目前，主流的深度学习框架都包含了自动梯度计算的功能，即我们可以只考虑网络结构并用代码实现，其梯度可以自动进行计算，无须人工干预，这样可以大幅提高开发效率．自动计算梯度的方法可以分为以下三类：数值微分、符号微分和自动微分．
由于这一部分内容对我目前而言并无太大的实际意义，主要是讲述了计算机怎么求导求梯度，所以简单了解一下，不做深究

优化问题

神经网络的参数学习比线性模型要更加困难，主要原因有两点

• 非凸优化问题
• 梯度消失问题

非凸优化问题

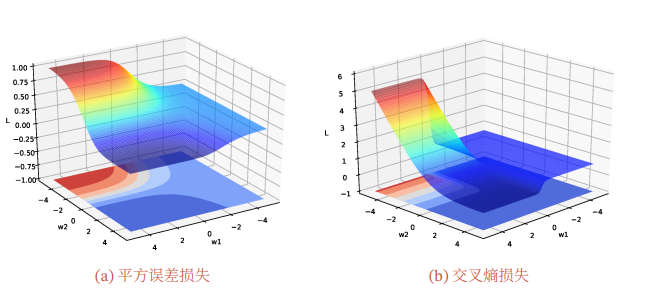
神经网络的优化问题是一个非凸优化问题。以一个最简单的1-1-1结构的两层神经网络为例

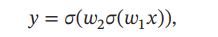
分别使用平方误差损失和交叉熵损失，损失函数与参数𝑤1和𝑤2的关系如图所示，可以看出两种损失函数都是关于参数的非凸函数．

梯度消失问题

误差从输出层反向传播时，在每一层都要乘以该层的激活函数的导数．当我们使用Sigmoid型函数：Logistic函数𝜎(𝑥)或Tanh函数时，Sigmoid型函数的导数的值域都小于或等于1，如图

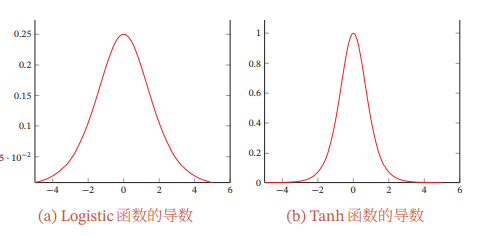
由于Sigmoid型函数的饱和性，饱和区的导数更是接近于 0．这样，误差经过每一层传递都会不断衰减．当网络层数很深时，梯度就会不停衰减，甚至消失，使得整个网络很难训练．这就是所谓的梯度消失问题（Vanishing GradientProblem），也称为梯度弥散问题．
在深度神经网络中，减轻梯度消失问题的方法有很多种．一种简单有效的方式是使用导数比较大的激活函数，比如ReLU等．
注意：饱和的意思通过查阅得知，就是一个函数的导数如果趋近于0，我就把这个函数称为饱和函数，导数如果向左趋近于0就称之为左趋近，反之就是右趋近

• 课后题：梯度消失问题是否可以通过增加学习率来缓解
  对此我的解释是：有一定效果，但不完全有效，因为梯度消失的本质是你函数设计导致导数容易偏低，多次累乘后导致消失，如果一开始把梯度强行拉大，也不能改变函数拉跨的本质，属于治标不治本

小结

前馈神经网络作为一种能力很强的非线性模型，其能力可以由通用近似定理来保证．前馈神经网络在20世纪80年代后期就已被广泛使用，但是大部分都采用两层网络结构（即一个隐藏层和一个输出层），神经元的激活函数基本上都是Sigmoid型函数，并且使用的损失函数也大多数是平方损失．虽然当时前馈神经网络的参数学习依然有很多难点，但其作为一种连接主义的典型模型，标志人工智能从高度符号化的知识期向低符号化的学习期开始转变．
我的锐评：确实难