【疑难杂症】协方差矩阵和矩阵相关系数的理解

前言

在做机器学习的过程中经常会有矩阵的相关运算，这里就比较典型的协方差和矩阵的相关系数做个自我的理解记录。
参考链接： https://blog.csdn.net/qq_29750461/article/details/81625470

协方差矩阵和矩阵相关系数

协方差#

如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值；如果两个变量的变化趋势相反，即其中一个变量大于自身的期望值时另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。
可以通俗的理解为：两个变量在变化过程中是同方向变化？还是反方向变化？同向或反向程度如何？
你变大，同时我也变大，说明两个变量是同向变化的，这时协方差就是正的;
你变大，同时我变小，说明两个变量是反向变化的，这时协方差就是负的;
从数值来看，协方差的数值越大，两个变量同向程度也就越大。反之亦然。

相关系数#

相关系数是用以反映变量之间相关关系密切程度的统计指标。相关系数也可以看成协方差：一种剔除了两个变量量纲影响、标准化后的特殊协方差,它消除了两个变量变化幅度的影响，而只是单纯反应两个变量每单位变化时的相似程度。
相关性可视化：

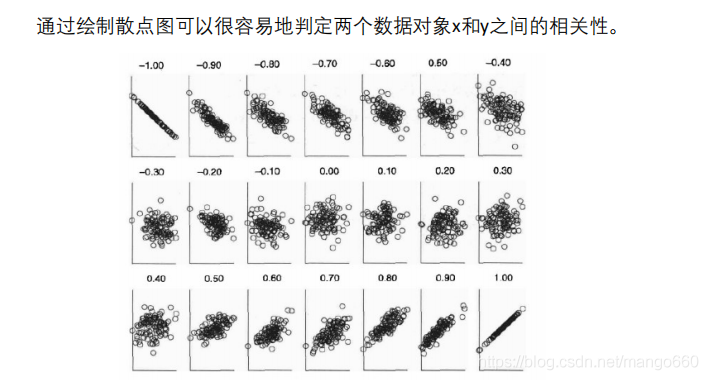
在统计学中，皮尔逊积矩相关系数是两个变量X和Y之间线性相关性的度量，给出了一个介于+1和-1之间的值，其中1表示完全正相关，0表示不相关，而-1表示完全负相关。在科学中，它被广泛用作两个变量之间线性依赖程度的度量