单调栈
503. 下一个更大元素 II

思路
可以使用单调栈解决本题。
单调栈中保存的是下标,从栈底到栈顶的下标在数组 nums 中对应的值是单调不升的。
每次我们移动到数组中的一个新的位置 i,我们就将当前单调栈中所有对应值小于 nums[i] 的下标弹出单调栈,这些值的下一个更大元素即为 nums[i]。
注意到只遍历一次序列是不够的,例如遍历序列 [2,3,1] 后元素 [1] 的下一个更大元素还是不知道。我们可以把这个循环数组「拉直」(处理时对下标取模),即复制该序列的前 n−1 个元素拼接在原序列的后面,将这个新序列当作普通序列继续处理。
代码
class Solution {
public int[] nextGreaterElements(int[] nums) {
int n = nums.length;
int[] ret = new int[n];
Arrays.fill(ret, -1);
Deque<Integer> stack = new LinkedList<Integer>();
for (int i = 0; i < n * 2 - 1; i++) {
while (!stack.isEmpty() && nums[stack.peek()] < nums[i % n]) {//while(){小于 nums[i] 的都下标弹出单调栈}
ret[stack.pop()] = nums[i % n];
}
stack.push(i % n);
}
return ret;
}
}
单调栈
单调栈简介
单调栈 Monotone Stack:栈内元素都是单调的,可以是单调递增或者单调递减,根据题目的具体情况决定。
- 单调递增栈可以找到元素向左遍历第一个比它小的元素。
- 单调递减栈可以找到元素向左遍历第一个比它大的元素。
优势
拥有线性的时间复杂度,所有的元素只会进栈一次,而且一旦出栈后就不会再进来了。
找到元素向左遍历第一个比它小的元素
84. 柱状图中最大的矩形
思路
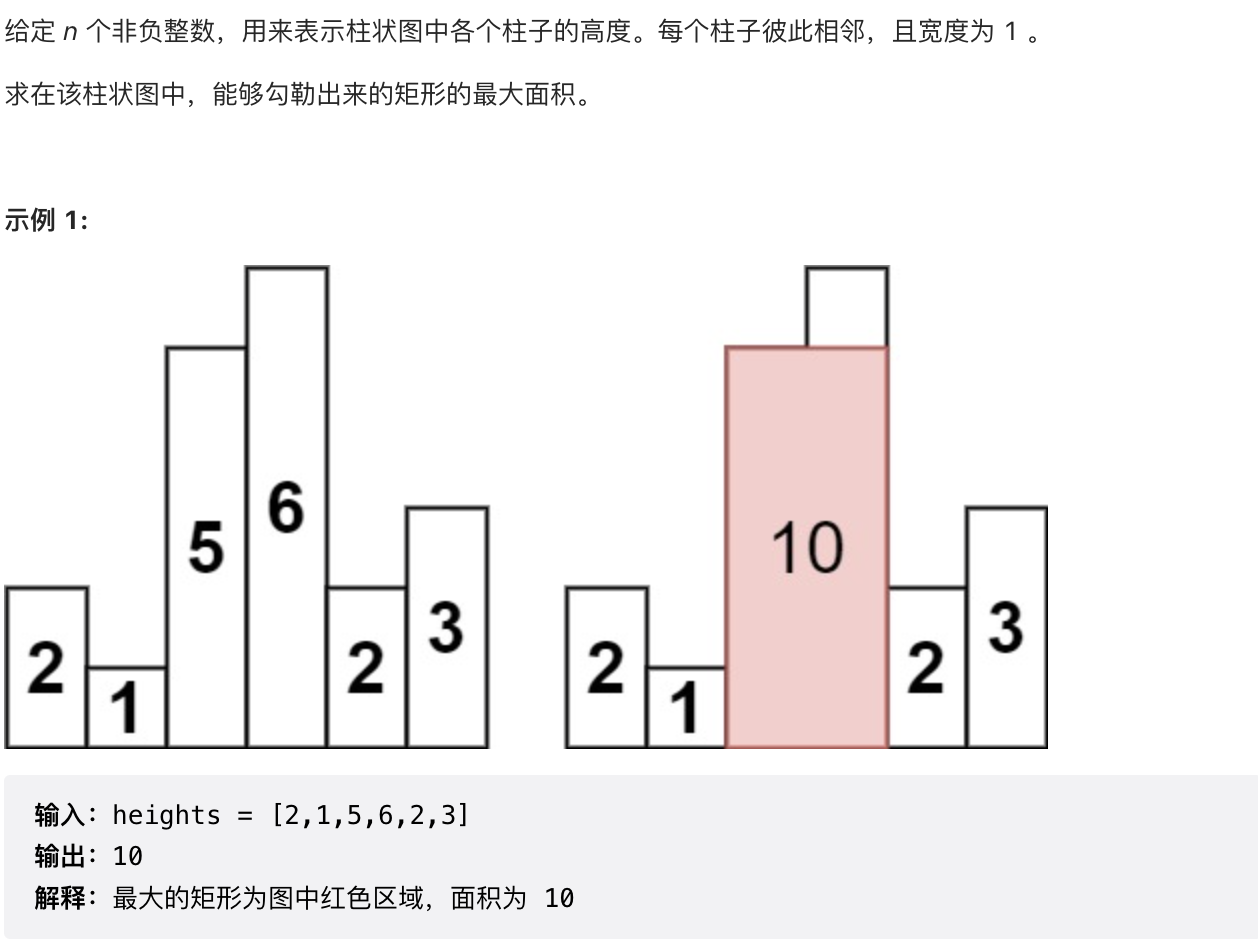
- 首先我们枚举某一根柱子 i 作为高 h = heights[i]
- 找到左右两侧最近的高度小于 h 的柱子 left 和 right,这样这两根柱子之间(不包括这两根柱子)的所有柱子高度均不小于 h,并且就是 i 能够扩展到的最远范围
当i=1时,左边界为-1;当i= heights.length-1,右边界为 heights.lengt - 两根柱子间的面积:(right - left - 1) * heights[i]
- 枚举所有的柱子取得最大的面积
代码
class Solution {
public int largestRectangleArea(int[] heights) {
Deque<Integer> st = new ArrayDeque<>();
int ans = 0;
for(int i=0;i<heights.length;i++){
while (!st.isEmpty() && heights[st.peek()] >= heights[i]){
int cur = st.poll();
int left = st.isEmpty()?-1:st.peek();
ans = Math.max(ans,(i - left -1)*heights[cur]);
}
st.push(i);
}
while (!st.isEmpty() && heights[st.peek()] >= 0){//遍历完发现是个递增数组
int cur = st.poll();
int left = st.isEmpty()?-1:st.peek();
ans = Math.max(ans,(heights.length - left -1)*heights[cur]);//此时右边界是数组最后的元素的右边,即heights.length
}
return ans;
}
}
找到元素向左遍历第一个比它大的元素
42. 接雨水

分析
动态规划:
- 用一个数组从左往右遍历的同时记录到位置i的最大值
- 从右往左遍历记录到位置i的最大值,同时判断此时的height[i]是否小于两边
- 若 height[i] 小于两边则计算能接的雨水量并加入结果
- 遍历结束之后即可得到能接的雨水总量
单调栈:
- 从左到右遍历数组,遍历到下标 i 时,如果栈内至少有两个元素,记栈顶元素为 top,top 的下面一个元素是 left,则一定有 height[left] ≥ height[top]
- 如果 height[i] > height[top],则得到一个可以接雨水的区域,该区域的宽度是 i-left-1,高度是 min(height[left], height[i]) - height[top],根据宽度和高度即可计算得到该区域能接的雨水量
代码
动态规划:
class Solution {
public int trap(int[] height) {
int[] leftMax = new int[height.length];
leftMax[0] = height[0];
for(int i=1;i<height.length;i++){
leftMax[i] = Math.max(leftMax[i-1],height[i]);
}
int ans = 0;
int rightMax = height[height.length-1];
for(int i=height.length-2;i>=0;i--){
rightMax = Math.max(rightMax,height[i]);
int mh = Math.min(leftMax[i],rightMax);
if(height[i]< mh) ans += (mh-height[i]);
}
return ans;
}
}
单调栈:
class Solution {
public int trap(int[] height) {
Deque<Integer> st = new ArrayDeque<>();
int ans = 0;
for(int i=0;i<height.length;i++){
while (!st.isEmpty() && height[st.peek()] < height[i]){
int top = st.pop();
if(!st.isEmpty()){
ans += (Math.min(height[st.peek()],height[i])- height[top]) * (i-st.peek()-1);
}
}
st.push(i);
}
return ans;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号