并查集
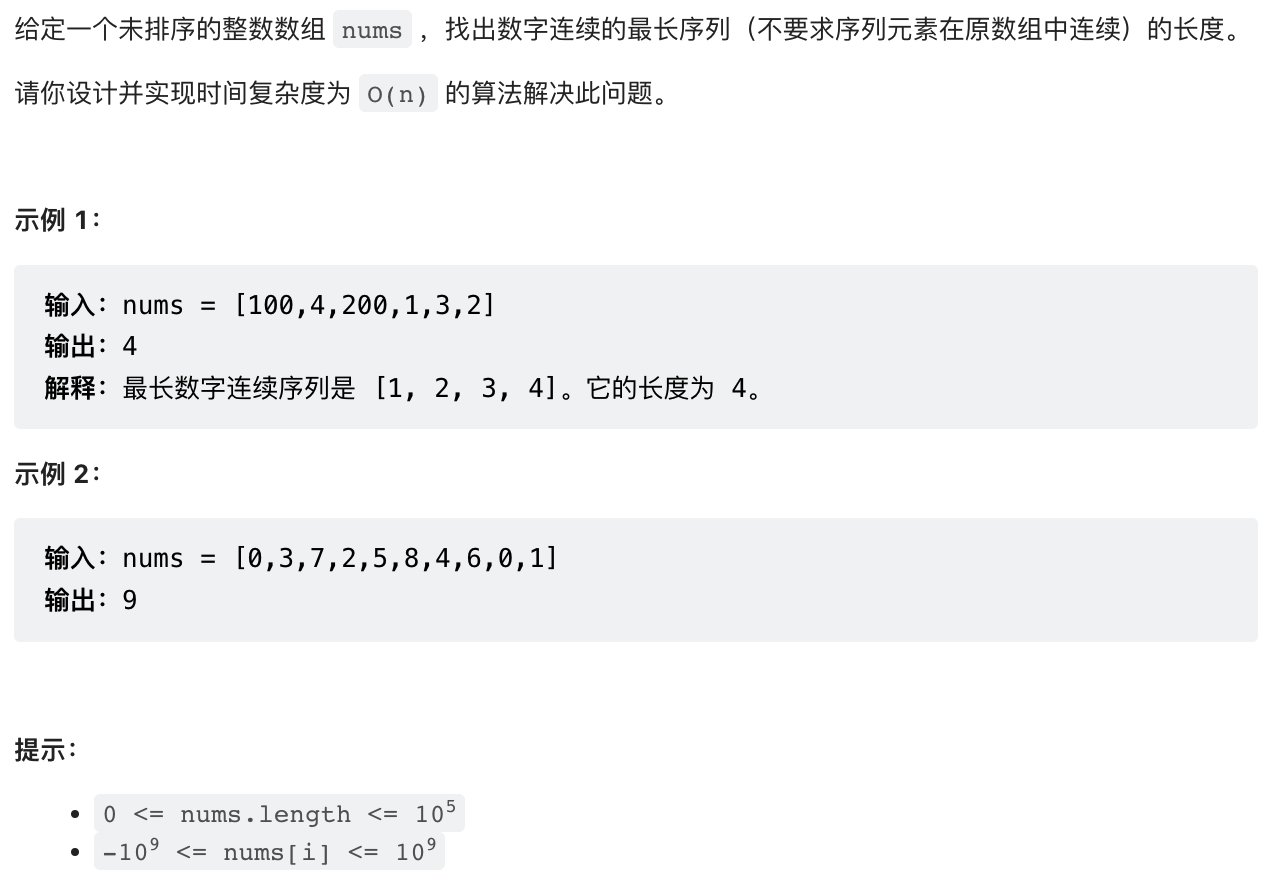
128. 最长连续序列
思路
方法1 最朴素的解法
先排序,从前往后找最长连续上升序列,但是复杂度已经至少有O(nlogn)。
方法2 哈希集合
外层需要枚举 O(n),只有当一个数是连续序列的第一个数的情况下才会进入内层循环
方法3 动态规划
哈希表记录连续区间长度
- 遍历nums数组中的所有数字num
- 当num是第一次出现时:
- 分别获取到左相邻数字num-1的连续区间长度left和右相邻数字num+1的连续区间长度right;
- 计算得到当前的区间长度为curLen=left+right+1curLen=left+right+1;
- 更新最长区间长度ans以及左右边界的区间长度。
方法4 并查集
记录右边界的,所有在一个连续区间内的元素都会在一个连通分量中,且这些元素的根结点都为最远的右边界元素。
- 遍历所有元素num,如果num+1存在,将num加入到num+1所在的连通分量中;
- 重新遍历一遍所有元素num,通过find函数找到num所在分量的根结点,也就是最远右边界,从而求得连续区间的长度。
代码
哈希集合
class Solution {
public int longestConsecutive(int[] nums) {
Set<Integer> num_set = new HashSet<Integer>();
for (int num : nums) {
num_set.add(num);
}
int longestStreak = 0;
for (int num : num_set) {
if (!num_set.contains(num - 1)) {
int currentNum = num;
int currentStreak = 1;
while (num_set.contains(currentNum + 1)) {
currentNum += 1;
currentStreak += 1;
}
longestStreak = Math.max(longestStreak, currentStreak);
}
}
return longestStreak;
}
}
动态规划
class Solution {
public int longestConsecutive(int[] nums) {
// key表示num,value表示num所在连续区间的长度
Map<Integer, Integer> map = new HashMap<>();
int ans = 0;
for (int num : nums) {
// 当map中不包含num,也就是num第一次出现
if (!map.containsKey(num)) {
// left为num-1所在连续区间的长度,更进一步理解为:左连续区间的长度
int left = map.getOrDefault(num - 1, 0);
// right为num+1所在连续区间的长度,更进一步理解为:右连续区间的长度
int right = map.getOrDefault(num + 1, 0);
// 当前连续区间的总长度
int curLen = left + right + 1;
ans = Math.max(ans, curLen);
// 将num加入map中,表示已经遍历过该值。其对应的value可以为任意值。
map.put(num, -1);
// 更新当前连续区间左边界和右边界对应的区间长度
map.put(num - left, curLen);
map.put(num + right, curLen);
}
}
return ans;
}
}
并查集
class UnionFind {
// 记录每个节点的父节点
private Map<Integer, Integer> parent;
public UnionFind(int[] nums) {
parent = new HashMap<>();
// 初始化父节点为自身
for (int num : nums) {
parent.put(num, num);
}
}
// 寻找x的父节点,实际上也就是x的最远连续右边界,这点类似于方法2
public Integer find(int x) {
// nums不包含x
if (!parent.containsKey(x)) {
return null;
}
// 遍历找到x的父节点
while (x != parent.get(x)) {
// 进行路径压缩,不写下面这行也可以,但是时间会慢些
parent.put(x, parent.get(parent.get(x)));
x = parent.get(x);
}
return x;
}
// 合并两个连通分量,在本题中只用来将num并入到num+1的连续区间中
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX == rootY) {
return;
}
parent.put(rootX, rootY);
}
}
class Solution {
public int longestConsecutive(int[] nums) {
UnionFind uf = new UnionFind(nums);
int ans = 0;
for (int num : nums) {
// 当num+1存在,将num合并到num+1所在集合中
if (uf.find(num + 1) != null) {
uf.union(num, num + 1);
}
}
for (int num : nums) {
// 找到num的最远连续右边界
int right = uf.find(num);
ans = Math.max(ans, right - num + 1);
}
return ans;
}
}
还可以加入了一个count哈希表,用于记录每个连通分量的节点个数,这样可在主函数一次遍历便可得到答案。
并查集
并查集的引入
并查集的重要思想在于,用集合中的一个元素代表集合。可以把集合比喻成帮派,而代表元素则是帮主。
最开始,大家各自为战。他们各自的帮主自然就是自己。

现在1号和3号比武,假设1号赢了,那么3号就认1号作帮主(合并1号和3号所在的集合,1号为代表元素)。

现在2号想和3号比武(合并3号和2号所在的集合),但3号表示,别跟我打,让我帮主来收拾你(合并代表元素)。不妨设这次又是1号赢了,那么2号也认1号做帮主。

现在假设4、5、6号也进行了一番帮派合并。

现在假设2号想与6号比。1号胜利后,4号认1号为帮主,他的手下也都是跟着投降了。

我们可以直接把它画成一棵树:

并查集的实现
最简单的并查集
class UnionFind {
int[] parent;
int[] rank;
int outlierNum;
// 初始化:一开始先将它们的父节点设为自己
public UnionFind(int n) {
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
// 查询:一层一层访问父节点,直至根节点(根节点的标志就是父节点是本身)
// 要判断两个元素是否属于同一个集合,只需要看它们的根节点是否相同即可
public int find(int x) {
if (parent[x] == x) {
return x;
} else {
parent[x] = find(parent[x]);
return parent[x];
}
}
// 合并:先找到两个集合的代表元素,然后将前者的父节点设为后者(也可以将后者的父节点设为前者)
public void merge(int x, int y) {
int i = find(x);
int j = find(y);
if (i == j) {
return;
}
parent[i] = j;
}
}
路径压缩
随着合并可能会形成一条长长的链,随着链越来越长,我们想要从底部找到根节点会变得越来越难。

使用路径压缩的方法,让每个元素到根节点的路径尽可能短,最好只需要一步:

我们需要在查询的过程中,把沿途的每个节点的父节点都设为根节点。
按秩合并
有些人可能有一个误解,以为路径压缩优化后,并查集始终都是一个菊花图(只有两层的树的俗称)。但其实由于路径压缩只在查询时进行,也只压缩一条路径,所以并查集最终的结构仍然可能是比较复杂的:

我们应该把简单的树往复杂的树上合并,而不是相反。因为这样合并后,到根节点距离变长的节点个数比较少。所以这时我们merge(7,8),要把8的父节点设为7。

代码
class UnionFind {
int[] parent;
int[] rank;
int outlierNum;
// 初始化
public UnionFind(int n) {
parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
rank = new int[n];
Arrays.fill(rank, 1);
outlierNum = n;
}
// 查询
public int find(int x) {
if (parent[x] == x) {
return x;
} else {
parent[x] = find(parent[x]);
return parent[x];
}
}
// 合并(按秩合并)
public void merge(int x, int y) {
int i = find(x);
int j = find(y);
if (i == j) {
return;
}
if (rank[i] > rank[j]) {
parent[j] = i;
} else {
parent[i] = j;
}
if (rank[i] == rank[j]) {
rank[i]++;
}
outlierNum--;
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号