回溯算法：求子集问题

78. 子集

给你一个整数数组nums，数组中的元素互不相同。返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。你可以按任意顺序返回解集。

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

输入：nums = [0]
输出：[[],[0]]

思路

如果把子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点！

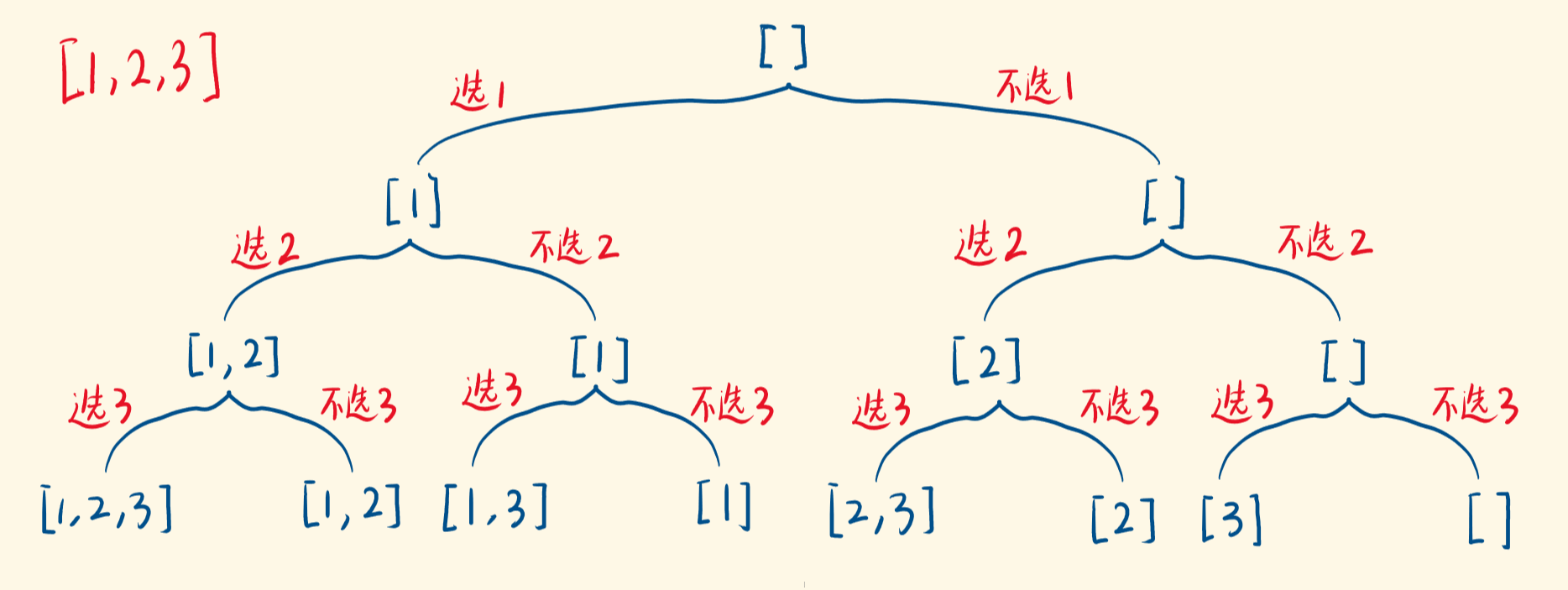
回溯三部曲

1.递归函数参数
全局变量temp为子集收集元素，ans存放子集组合。
取过的元素不会重复取，写回溯算法的时候，for就要从startIndex开始，而不是从0开始。

    List<Integer> temp = new ArrayList<Integer>();
    List<List<Integer>> ans = new ArrayList<List<Integer>>();
    private void backtracking(int[] nums, int startIndex) {}

2.递归终止条件
剩余集合为空的时候，就是叶子节点。就是startIndex已经大于数组的长度了，就终止了，因为没有元素可取了。

3.单层搜索逻辑
求取子集问题，不需要任何剪枝！因为子集就是要遍历整棵树。

代码

class Solution {
    List<Integer> temp = new ArrayList<Integer>();
    List<List<Integer>> ans = new ArrayList<List<Integer>>();

    public List<List<Integer>> subsets(int[] nums) {
        backtracking(nums,0);
        return ans;
    }
    private void backtracking(int[] nums, int startIndex) {
        ans.add(new ArrayList<>(temp)); // 收集子集
        if (startIndex >= nums.length) { // 终止条件可以不加
            return;
        }
        for (int i = startIndex; i < nums.length; i++) {
            temp.add(nums[i]);
            backtracking(nums, i + 1);
            temp.remove(temp.size()-1);
        }
    }
}