回溯算法：求组合总和（二）

40. 组合总和 II

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：

• 所有数字（包括目标数）都是正整数
• 解集不能包含重复的组合

输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
  [1,2,2],
  [5]
]

思路

难点在于：集合（数组candidates）有重复元素，但还不能有重复的组合。

可以把所有组合求出来，再用set或者map去重，但这么做很容易超时，所以要在搜索的过程中就去掉重复组合。

在题目中，元素在同一个组合内是可以重复的，但两个组合不能相同。所以我们要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。

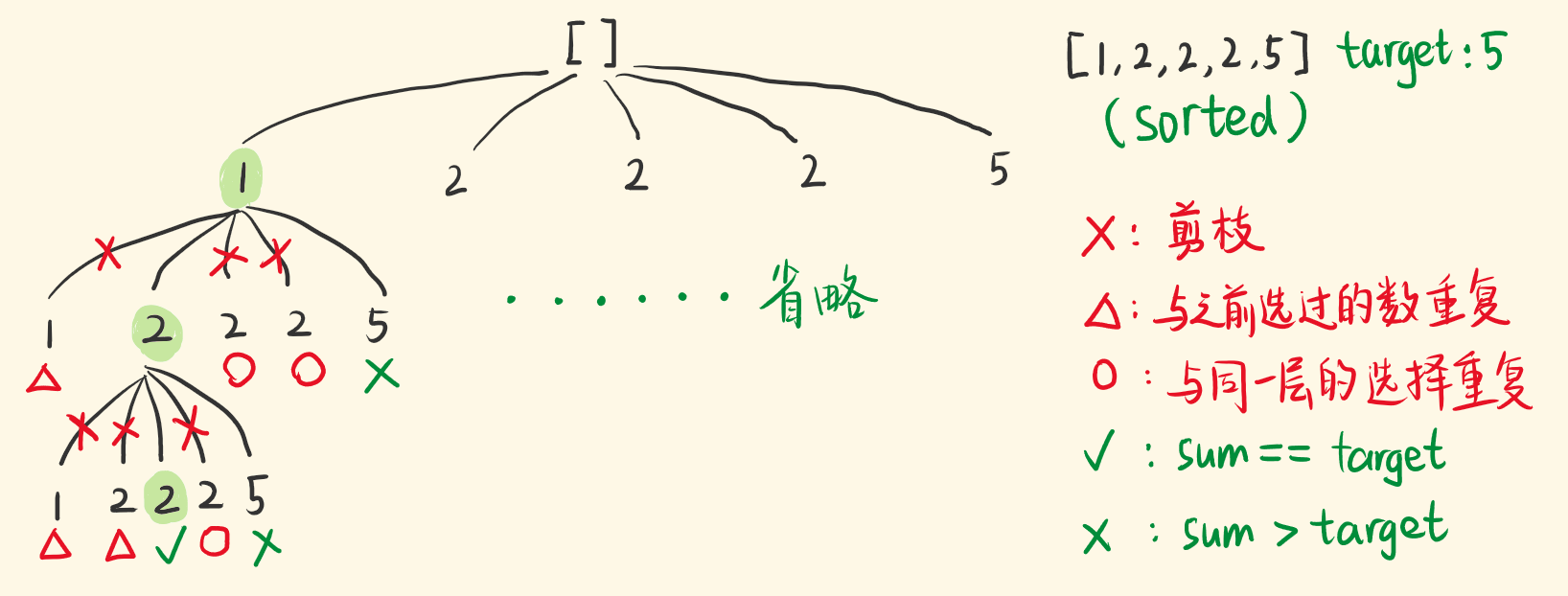
代码

class Solution {
    List<Integer> temp = new ArrayList<Integer>();
    List<List<Integer>> ans = new ArrayList<List<Integer>>();

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        boolean[] used = new boolean[candidates.length];
        // 首先把给candidates排序，让其相同的元素都挨在一起
        Arrays.sort(candidates);
        backtracking(candidates,target,0,0,used);
        return ans;
    }
    private void backtracking(int[] candidates, int target,int sum,int begin,boolean[] used) {
        if (sum == target) {
            ans.add(new ArrayList<>(temp));
            return;
        }

        // 遍历可能的搜索起点
        for (int i=begin;i<candidates.length && sum + candidates[i] <= target;i++) {
            // used[i - 1] == true，说明同一树支candidates[i - 1]使用过
            // used[i - 1] == false，说明同一树层candidates[i - 1]使用过

            // 而我们要对同一树层使用过的元素进行跳过
            if (i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false) {
                continue;
            }
            temp.add(candidates[i]);
            used[i] = true;
            // 下一轮搜索
            backtracking(candidates, target,sum+candidates[i],i+1,used);
            used[i] = false;
            // 回头的过程
            temp.remove(temp.size() - 1);
        }
    }
}