回溯算法：求组合问题

77. 组合

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

输入: n = 4, k = 2
输出:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

思路

本题这是回溯法的经典题目。

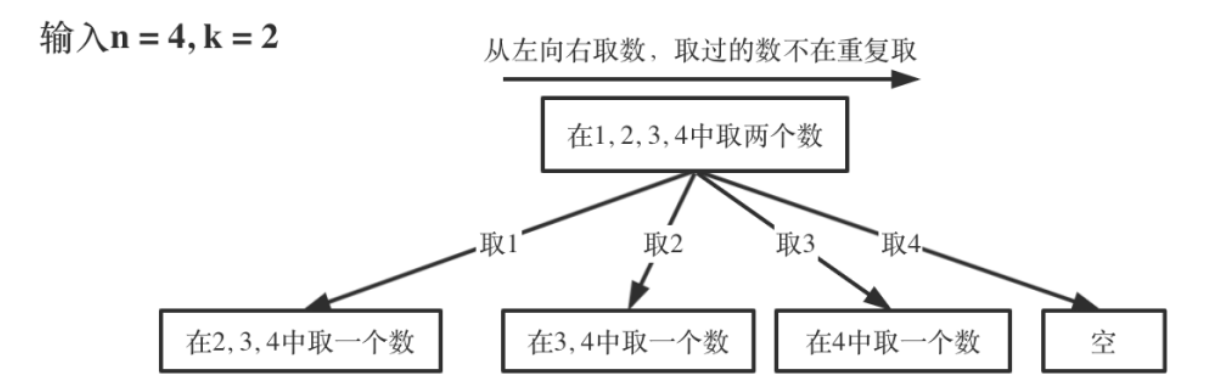
每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围。

代码

class Solution {
    List<Integer> temp = new ArrayList<Integer>();
    List<List<Integer>> ans = new ArrayList<List<Integer>>();
    
    public List<List<Integer>> combine(int n, int k) {
        if (k <= 0 || n < k) {
            return ans;
        }
        backtracking(n, k, 1);
        return ans;
    }

    private void backtracking(int n, int k, int begin) {
        // 递归终止条件
        if (temp.size() == k) {
            ans.add(new ArrayList<>(temp));
            return;
        }

        // 遍历可能的搜索起点
        for (int i = begin; i <= n; i++) {
            // 向temp变量里添加一个数
            temp.add(i);
            // 下一轮搜索，设置的搜索起点要加 1，因为组合数理不允许出现重复的元素
            backtracking(n, k, i + 1);
            // 重点理解这里：深度优先遍历有回头的过程，因此递归之前做了什么，递归之后需要做相同操作的逆向操作
            temp.remove(temp.size() - 1);
        }
    }
}