前缀树
208. 实现 Trie (前缀树)
Trie(发音类似 "try")或者说前缀树是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
- Trie() 初始化前缀树对象
- void insert(String word) 向前缀树中插入字符串 word
- boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false
- boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false
输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]
解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 True
trie.search("app"); // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app"); // 返回 True
思路
Trie,又称前缀树或字典树,每个枝干上有26个分支代表26个字母。
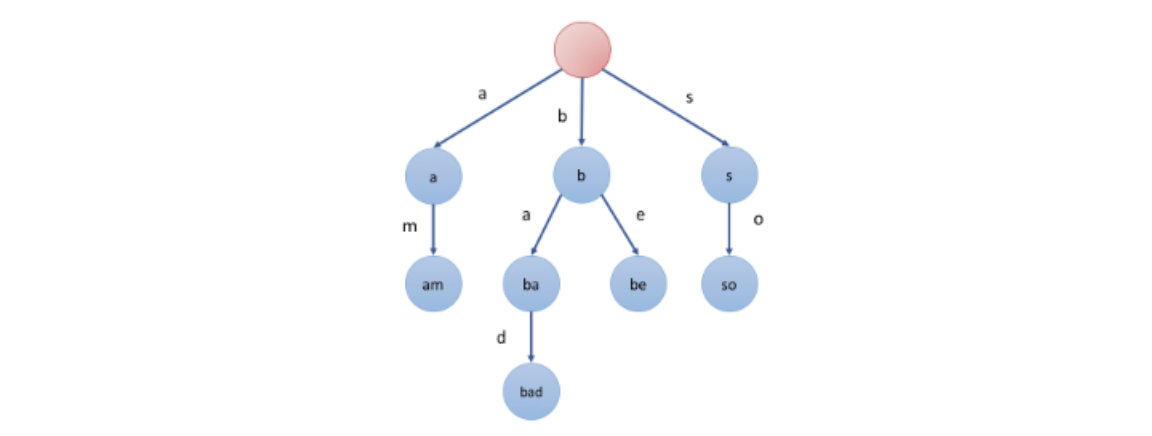
其每个节点包含以下字段:
- 指针数组 children
题中说了word 和 prefix 仅由小写英文字母组成,可以把它看做是一颗26叉树,即小写英文字母的数量。 - 布尔字段 isEnd
表示该节点是否为字符串的结尾。
插入字符串,有两种情况:
- 子节点存在
沿着指针移动到子节点,继续处理下一个字符。 - 子节点不存在
创建一个新的子节点,记录在 children 数组的对应位置上,然后沿着指针移动到子节点,继续搜索下一个字符。
查找前缀,有两种情况:
- 子节点存在
沿着指针移动到子节点,继续搜索下一个字符。 - 子节点不存在
说明字典树中不包含该前缀,返回空指针。
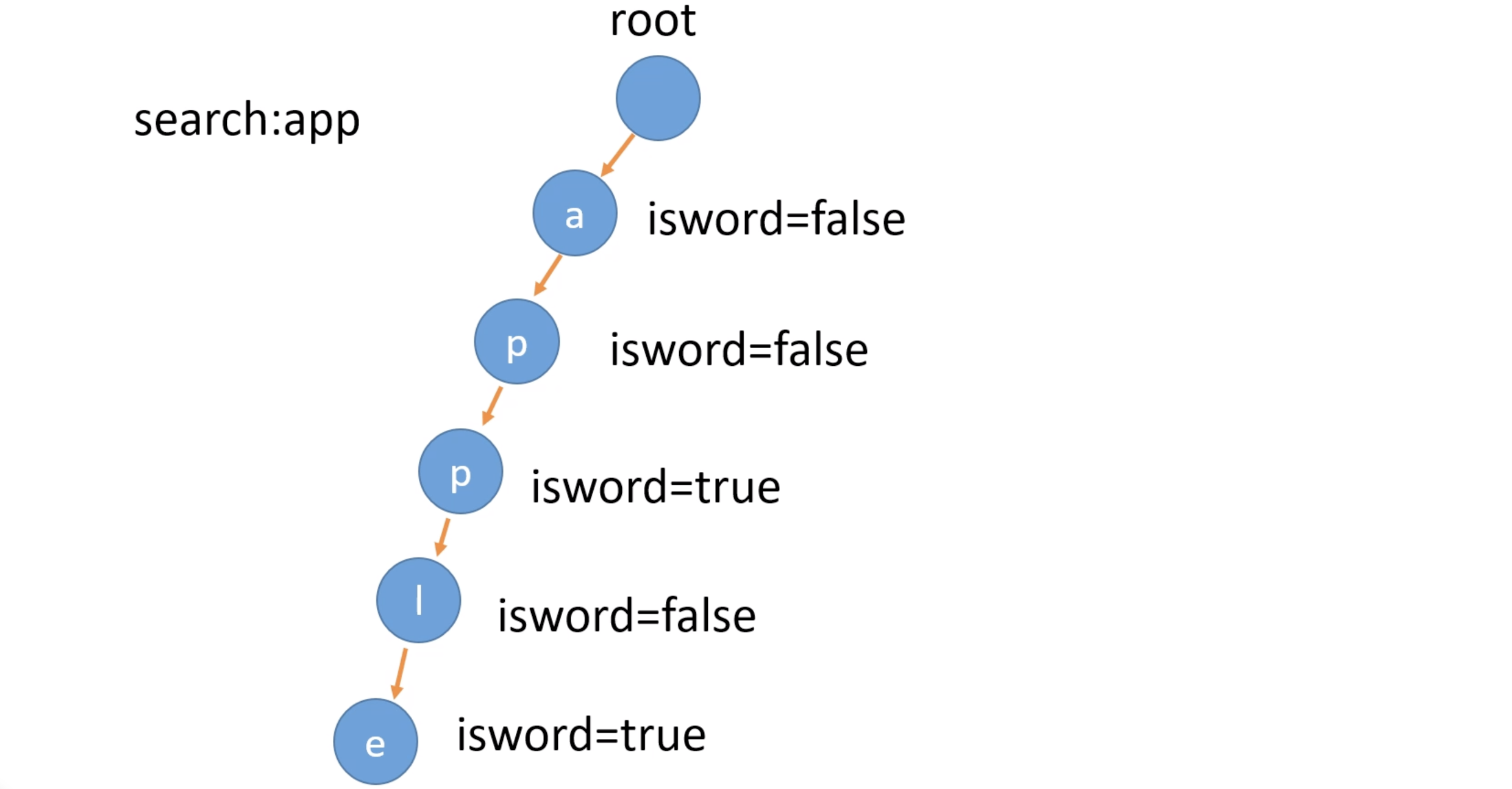
代码
class Trie {
private Trie[] children;
private boolean isEnd;
public Trie() {
children = new Trie[26];
isEnd = false;
}
public void insert(String word) {
Trie node = this;
for (int i = 0; i < word.length(); i++) {
char ch = word.charAt(i);
int index = ch - 'a';
if (node.children[index] == null) {
node.children[index] = new Trie();
}
node = node.children[index];
}
node.isEnd = true;
}
public boolean search(String word) {
Trie node = searchPrefix(word);
return node != null && node.isEnd;
}
public boolean startsWith(String prefix) {
return searchPrefix(prefix) != null;
}
private Trie searchPrefix(String prefix) {
Trie node = this;
for (int i = 0; i < prefix.length(); i++) {
char ch = prefix.charAt(i);
int index = ch - 'a';
if (node.children[index] == null) {
return null;
}
node = node.children[index];
}
return node;
}
}
前缀树
440. 字典序的第K小数字

分析
字典树的先序遍历就是字典序。
n=12时的字典树,找到第5小的数:
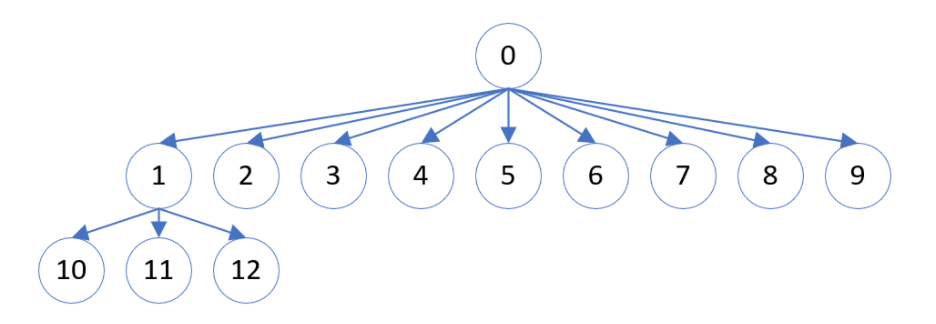
前序遍历该字典树,到第 5 个节点找到2,即为第 5 小的数字。
实际不需要构造整颗字典树来遍历,可以通过计算得到某个节点下的子树节点的总数而跳过遍历的时间。
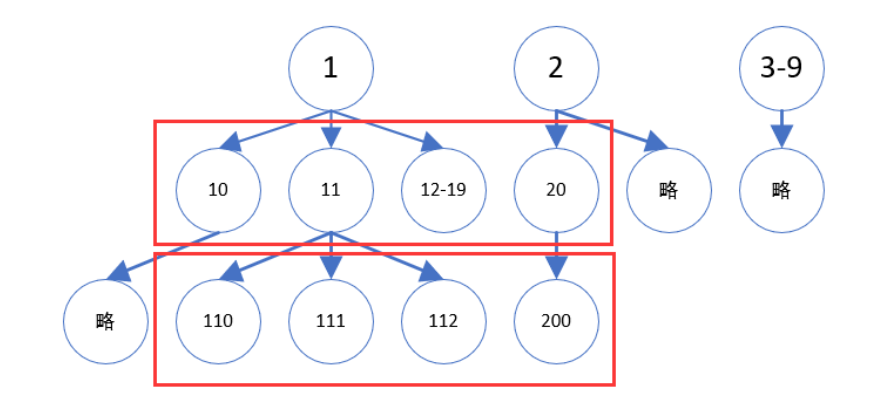
假定我们存在某个函数 int getSteps(int curr, long n),该函数实现了统计范围 [1, n] 内以 curr 为前缀的数的个数。
从最小的前缀 1 开始枚举,假设当前枚举到前缀 curr,steps = getSteps(curr,n):
- steps<k:说明所有以 curr 为前缀的数组均可跳过,此时让 curr 自增,k 减去 steps。从下一个「数值比 curr 大」的前缀中找目标值;
- steps⩾k:说明目标值前缀必然为 curr,此时我们需要在以 curr 为前缀的前提下找目标值。此时让 curr 乘 10,k 减 1(代表跳过了 curr 本身)。从下一个「字典序比 curr 大」的前缀中找目标值。
代码
class Solution {
public int findKthNumber(int n, int k) {
int cur = 1;
while(k>1){
int steps = getSteps(cur,n);//以 i 为根节点构成的子树的节点数目为 steps(i)
if(steps < k){
k -= steps;
cur++;
}else {
cur = cur * 10;
k--;
}
}
return cur;
}
public int getSteps(int cur,long n){
int steps = 0;
long first = cur,last = cur;
while(first <= n){
steps += Math.min(last,n) - first + 1;//把根节点算进去了
first = first * 10;
last = last * 10 + 9;
}
return steps;
}
}





