分割数据集和优化梯度下降算法
优化算法
import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasets
import opt_utils # help function
import testCase # help function
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
Gradient Descent
def update_parameters_with_gd(parameters, grads, learning_rate):
"""
Update parameters using one step of gradient descent
Arguments:
parameters -- python dictionary containing your parameters to be updated:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients to update each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
learning_rate -- the learning rate, scalar.
Returns:
parameters -- python dictionary containing your updated parameters
"""
L = len(parameters) // 2
for l in range(L):
parameters['W' + str(l+1)] = parameters['W' + str(l+1)] - learning_rate * grads['dW' + str(l+1)]
parameters['b' + str(l+1)] = parameters['b' + str(l+1)] - learning_rate * grads['db' + str(l+1)]
return parameters
parameters , grads , learning_rate = testCase.update_parameters_with_gd_test_case()
parameters = update_parameters_with_gd(parameters,grads,learning_rate)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
W1 = [[ 1.63535156 -0.62320365 -0.53718766]
[-1.07799357 0.85639907 -2.29470142]]
b1 = [[ 1.74604067]
[-0.75184921]]
W2 = [[ 0.32171798 -0.25467393 1.46902454]
[-2.05617317 -0.31554548 -0.3756023 ]
[ 1.1404819 -1.09976462 -0.1612551 ]]
b2 = [[-0.88020257]
[ 0.02561572]
[ 0.57539477]]
Mini-Batch Gradient descent
def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
"""
Creates a list of random minibatches from (X, Y)
Arguments:
X -- input data, of shape (input size, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
mini_batch_size -- size of the mini-batches, integer
Returns:
mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)
"""
np.random.seed(seed)
m = X.shape[1] # number of training examples
mini_batches = []
# Step 1: Shuffle (X, Y)
permutation = list(np.random.permutation(m)) # 它会返回一个长度为m的随机数组,且里面的数是0到m-1
shuffled_X = X[:,permutation] # 将每一列的数据按permutation的顺序来重新排列。
shuffled_Y = Y[:,permutation].reshape((1,m))
# Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.
num_complete_minibatches = math.floor(m / mini_batch_size) #分割成训练集(floor:值是99.99,那么返回99,剩下的0.99会被舍弃)
for k in range(0, num_complete_minibatches):
mini_batch_X = shuffled_X[:, k * mini_batch_size : (k+1) * mini_batch_size]
mini_batch_Y = shuffled_Y[:, k * mini_batch_size : (k+1) * mini_batch_size]
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
if m % mini_batch_size != 0:
mini_batch_X = shuffled_X[:, num_complete_minibatches*mini_batch_size : m]
mini_batch_Y = shuffled_Y[:, num_complete_minibatches*mini_batch_size : m]
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
return mini_batches
X_assess, Y_assess, mini_batch_size = testCase.random_mini_batches_test_case()
mini_batches = random_mini_batches(X_assess, Y_assess, mini_batch_size)
print ("shape of the 1st mini_batch_X: " + str(mini_batches[0][0].shape))
print ("shape of the 2nd mini_batch_X: " + str(mini_batches[1][0].shape))
print ("shape of the 3rd mini_batch_X: " + str(mini_batches[2][0].shape))
print ("shape of the 1st mini_batch_Y: " + str(mini_batches[0][1].shape))
print ("shape of the 2nd mini_batch_Y: " + str(mini_batches[1][1].shape))
print ("shape of the 3rd mini_batch_Y: " + str(mini_batches[2][1].shape))
print ("mini batch sanity check: " + str(mini_batches[0][0][0][0:3]))
shape of the 1st mini_batch_X: (12288, 64)
shape of the 2nd mini_batch_X: (12288, 64)
shape of the 3rd mini_batch_X: (12288, 20)
shape of the 1st mini_batch_Y: (1, 64)
shape of the 2nd mini_batch_Y: (1, 64)
shape of the 3rd mini_batch_Y: (1, 20)
mini batch sanity check: [ 0.90085595 -0.7612069 0.2344157 ]
Momentum
def initialize_velocity(parameters):
"""
Initializes the velocity as a python dictionary with:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
Arguments:
parameters -- python dictionary containing your parameters.
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
Returns:
v -- python dictionary containing the current velocity.
v['dW' + str(l)] = velocity of dWl
v['db' + str(l)] = velocity of dbl
"""
L = len(parameters) // 2
v = {}
for l in range(L):
v['dW' + str(l+1)] = np.zeros(parameters['W' + str(l+1)].shape)
v['db' + str(l+1)] = np.zeros(parameters['b' + str(l+1)].shape)
return v
parameters = testCase.initialize_velocity_test_case()
v = initialize_velocity(parameters)
print('v["dW1"] = ' + str(v["dW1"]))
print('v["db1"] = ' + str(v["db1"]))
print('v["dW2"] = ' + str(v["dW2"]))
print('v["db2"] = ' + str(v["db2"]))
v["dW1"] = [[0. 0. 0.]
[0. 0. 0.]]
v["db1"] = [[0.]
[0.]]
v["dW2"] = [[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]]
v["db2"] = [[0.]
[0.]
[0.]]
影响梯度的方向,需要使用以下公式:

def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
"""
Update parameters using Momentum
Arguments:
parameters -- python dictionary containing your parameters:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- python dictionary containing the current velocity:
v['dW' + str(l)] = ...
v['db' + str(l)] = ...
beta -- the momentum hyperparameter, scalar
learning_rate -- the learning rate, scalar
Returns:
parameters -- python dictionary containing your updated parameters
v -- python dictionary containing your updated velocities
"""
L = len(parameters) // 2
for l in range(L):
v["dW" + str(l+1)] = beta*v["dW" + str(l+1)] + (1-beta)*grads["dW" + str(l+1)] # 包含计算出来的grads
v["db" + str(l+1)] = beta*v["db" + str(l+1)] + (1-beta)*grads["db" + str(l+1)]
# update parameters
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate*v["dW" + str(l+1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate*v["db" + str(l+1)]
return parameters, v
parameters,grads,v = testCase.update_parameters_with_momentum_test_case()
update_parameters_with_momentum(parameters,grads,v,beta=0.9,learning_rate=0.01)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
print('v["dW1"] = ' + str(v["dW1"]))
print('v["db1"] = ' + str(v["db1"]))
print('v["dW2"] = ' + str(v["dW2"]))
print('v["db2"] = ' + str(v["db2"]))
W1 = [[ 1.62544598 -0.61290114 -0.52907334]
[-1.07347112 0.86450677 -2.30085497]]
b1 = [[ 1.74493465]
[-0.76027113]]
W2 = [[ 0.31930698 -0.24990073 1.4627996 ]
[-2.05974396 -0.32173003 -0.38320915]
[ 1.13444069 -1.0998786 -0.1713109 ]]
b2 = [[-0.87809283]
[ 0.04055394]
[ 0.58207317]]
v["dW1"] = [[-0.11006192 0.11447237 0.09015907]
[ 0.05024943 0.09008559 -0.06837279]]
v["db1"] = [[-0.01228902]
[-0.09357694]]
v["dW2"] = [[-0.02678881 0.05303555 -0.06916608]
[-0.03967535 -0.06871727 -0.08452056]
[-0.06712461 -0.00126646 -0.11173103]]
v["db2"] = [[0.02344157]
[0.16598022]
[0.07420442]]
Note that:
- 速度v是用0来初始化的,因此算法需要经过几次迭代才能把速度提升上来开始跨越更大步伐。
- 当beta=0时,相当于没有使用momentum算法的标准的梯度下降算法。
- 当beta越大的时候,说明平滑的作用越明显。通常0.9是比较合适的值。
Adam
Adam算法是训练神经网络中最有效的算法之一,它是RMSProp算法与Momentum算法的结合体。
def initialize_adam(parameters) :
"""
Initializes v and s as two python dictionaries with:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
Arguments:
parameters -- python dictionary containing your parameters.
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
Returns:
v -- python dictionary that will contain the exponentially weighted average of the gradient.
v["dW" + str(l)] = ...
v["db" + str(l)] = ...
s -- python dictionary that will contain the exponentially weighted average of the squared gradient.
s["dW" + str(l)] = ...
s["db" + str(l)] = ...
"""
L = len(parameters) // 2 # number of layers in the neural networks
v = {}
s = {}
# Initialize v, s. Input: "parameters". Outputs: "v, s".
for l in range(L):
v["dW" + str(l+1)] = np.zeros(parameters["W" + str(l+1)].shape)
v["db" + str(l+1)] = np.zeros(parameters["b" + str(l+1)].shape)
s["dW" + str(l+1)] = np.zeros(parameters["W" + str(l+1)].shape)
s["db" + str(l+1)] = np.zeros(parameters["b" + str(l+1)].shape)
return v, s
parameters = testCase.initialize_adam_test_case()
v,s = initialize_adam(parameters)
print('v["dW1"] = ' + str(v["dW1"]))
print('v["db1"] = ' + str(v["db1"]))
print('v["dW2"] = ' + str(v["dW2"]))
print('v["db2"] = ' + str(v["db2"]))
print('s["dW1"] = ' + str(s["dW1"]))
print('s["db1"] = ' + str(s["db1"]))
print('s["dW2"] = ' + str(s["dW2"]))
print('s["db2"] = ' + str(s["db2"]))
v["dW1"] = [[0. 0. 0.]
[0. 0. 0.]]
v["db1"] = [[0.]
[0.]]
v["dW2"] = [[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]]
v["db2"] = [[0.]
[0.]
[0.]]
s["dW1"] = [[0. 0. 0.]
[0. 0. 0.]]
s["db1"] = [[0.]
[0.]]
s["dW2"] = [[0. 0. 0.]
[0. 0. 0.]
[0. 0. 0.]]
s["db2"] = [[0.]
[0.]
[0.]]
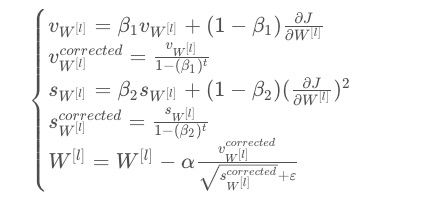
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01,
beta1 = 0.9, beta2 = 0.999, epsilon = 1e-8):
"""
Update parameters using Adam
Arguments:
parameters -- python dictionary containing your parameters:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
learning_rate -- the learning rate, scalar.
beta1 -- Exponential decay hyperparameter for the first moment estimates
beta2 -- Exponential decay hyperparameter for the second moment estimates
epsilon -- hyperparameter preventing division by zero in Adam updates
Returns:
parameters -- python dictionary containing your updated parameters
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
"""
L = len(parameters) // 2
v_corrected = {} #偏差修正后的值
s_corrected = {} #偏差修正后的值
for l in range(L):
#梯度的移动平均值,输入:"v , grads , beta1",输出:" v "
v["dW" + str(l + 1)] = beta1 * v["dW" + str(l + 1)] + (1 - beta1) * grads["dW" + str(l + 1)]
v["db" + str(l + 1)] = beta1 * v["db" + str(l + 1)] + (1 - beta1) * grads["db" + str(l + 1)]
#计算第一阶段的偏差修正后的估计值,输入"v , beta1 , t" , 输出:"v_corrected"
v_corrected["dW" + str(l + 1)] = v["dW" + str(l + 1)] / (1 - np.power(beta1,t))
v_corrected["db" + str(l + 1)] = v["db" + str(l + 1)] / (1 - np.power(beta1,t))
#计算平方梯度的移动平均值,输入:"s, grads , beta2",输出:"s"
s["dW" + str(l + 1)] = beta2 * s["dW" + str(l + 1)] + (1 - beta2) * np.square(grads["dW" + str(l + 1)])
s["db" + str(l + 1)] = beta2 * s["db" + str(l + 1)] + (1 - beta2) * np.square(grads["db" + str(l + 1)])
#计算第二阶段的偏差修正后的估计值,输入:"s , beta2 , t",输出:"s_corrected"
s_corrected["dW" + str(l + 1)] = s["dW" + str(l + 1)] / (1 - np.power(beta2,t))
s_corrected["db" + str(l + 1)] = s["db" + str(l + 1)] / (1 - np.power(beta2,t))
#更新参数,输入: "parameters, learning_rate, v_corrected, s_corrected, epsilon". 输出: "parameters".
parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * (v_corrected["dW" + str(l + 1)] / np.sqrt(s_corrected["dW" + str(l + 1)] + epsilon))
parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * (v_corrected["db" + str(l + 1)] / np.sqrt(s_corrected["db" + str(l + 1)] + epsilon))
return (parameters,v,s)
parameters , grads , v , s = testCase.update_parameters_with_adam_test_case()
update_parameters_with_adam(parameters,grads,v,s,t=2)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
print('v["dW1"] = ' + str(v["dW1"]))
print('v["db1"] = ' + str(v["db1"]))
print('v["dW2"] = ' + str(v["dW2"]))
print('v["db2"] = ' + str(v["db2"]))
print('s["dW1"] = ' + str(s["dW1"]))
print('s["db1"] = ' + str(s["db1"]))
print('s["dW2"] = ' + str(s["dW2"]))
print('s["db2"] = ' + str(s["db2"]))
W1 = [[ 1.63178673 -0.61919778 -0.53561312]
[-1.08040999 0.85796626 -2.29409733]]
b1 = [[ 1.75225313]
[-0.75376553]]
W2 = [[ 0.32648046 -0.25681174 1.46954931]
[-2.05269934 -0.31497584 -0.37661299]
[ 1.14121081 -1.09245036 -0.16498684]]
b2 = [[-0.88529978]
[ 0.03477238]
[ 0.57537385]]
v["dW1"] = [[-0.11006192 0.11447237 0.09015907]
[ 0.05024943 0.09008559 -0.06837279]]
v["db1"] = [[-0.01228902]
[-0.09357694]]
v["dW2"] = [[-0.02678881 0.05303555 -0.06916608]
[-0.03967535 -0.06871727 -0.08452056]
[-0.06712461 -0.00126646 -0.11173103]]
v["db2"] = [[0.02344157]
[0.16598022]
[0.07420442]]
s["dW1"] = [[0.00121136 0.00131039 0.00081287]
[0.0002525 0.00081154 0.00046748]]
s["db1"] = [[1.51020075e-05]
[8.75664434e-04]]
s["dW2"] = [[7.17640232e-05 2.81276921e-04 4.78394595e-04]
[1.57413361e-04 4.72206320e-04 7.14372576e-04]
[4.50571368e-04 1.60392066e-07 1.24838242e-03]]
s["db2"] = [[5.49507194e-05]
[2.75494327e-03]
[5.50629536e-04]]
Model with different optimization algorithms
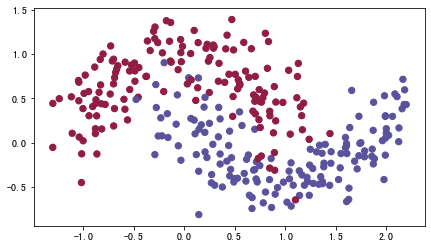
train_X, train_Y = opt_utils.load_dataset(is_plot=True)
def model(X,Y,layers_dims,optimizer,learning_rate=0.0007,
mini_batch_size=64,beta=0.9,beta1=0.9,beta2=0.999,
epsilon=1e-8,num_epochs=10000,print_cost=True,is_plot=True):
"""
可以运行在不同优化器模式下的3层神经网络模型。
参数:
X - 输入数据,维度为(2,输入的数据集里面样本数量)
Y - 与X对应的标签
layers_dims - 包含层数和节点数量的列表
optimizer - 字符串类型的参数,用于选择优化类型,【 "gd" | "momentum" | "adam" 】
learning_rate - 学习率
mini_batch_size - 每个小批量数据集的大小
beta - 用于动量优化的一个超参数
beta1 - 用于计算梯度后的指数衰减的估计的超参数
beta1 - 用于计算平方梯度后的指数衰减的估计的超参数
epsilon - 用于在Adam中避免除零操作的超参数,一般不更改
num_epochs - 整个训练集的遍历次数,(视频2.9学习率衰减,1分55秒处,视频中称作“代”),相当于之前的num_iteration
print_cost - 是否打印误差值,每遍历1000次数据集打印一次,但是每100次记录一个误差值,又称每1000代打印一次
is_plot - 是否绘制出曲线图
返回:
parameters - 包含了学习后的参数
"""
L = len(layers_dims)
costs = []
t = 0 #每学习完一个minibatch就增加1
seed = 10 #随机种子
#初始化参数
parameters = opt_utils.initialize_parameters(layers_dims)
#选择优化器
if optimizer == "gd":
pass #不使用任何优化器,直接使用梯度下降法
elif optimizer == "momentum":
v = initialize_velocity(parameters) #使用动量
elif optimizer == "adam":
v, s = initialize_adam(parameters)#使用Adam优化
else:
print("optimizer参数错误,程序退出。")
exit(1)
#开始学习
for i in range(num_epochs):
#定义随机 minibatches,我们在每次遍历数据集之后增加种子以重新排列数据集,使每次数据的顺序都不同
seed = seed + 1
minibatches = random_mini_batches(X,Y,mini_batch_size,seed)
for minibatch in minibatches:
#选择一个minibatch
(minibatch_X,minibatch_Y) = minibatch
#前向传播
A3 , cache = opt_utils.forward_propagation(minibatch_X,parameters)
#计算误差
cost = opt_utils.compute_cost(A3 , minibatch_Y)
#反向传播
grads = opt_utils.backward_propagation(minibatch_X,minibatch_Y,cache)
#更新参数
if optimizer == "gd":
parameters = update_parameters_with_gd(parameters,grads,learning_rate)
elif optimizer == "momentum":
parameters, v = update_parameters_with_momentum(parameters,grads,v,beta,learning_rate)
elif optimizer == "adam":
t = t + 1
parameters , v , s = update_parameters_with_adam(parameters,grads,v,s,t,learning_rate,beta1,beta2,epsilon)
#记录误差值
if i % 100 == 0:
costs.append(cost)
#是否打印误差值
if print_cost and i % 1000 == 0:
print("第" + str(i) + "次遍历整个数据集,当前误差值:" + str(cost))
#是否绘制曲线图
if is_plot:
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('epochs (per 100)')
plt.title("Learning rate = " + str(learning_rate))
plt.show()
return parameters
Mini-batch Gradient descent
layers_dims = [train_X.shape[0],5,2,1]
parameters = model(train_X, train_Y, layers_dims, optimizer="gd",is_plot=True)
第0次遍历整个数据集,当前误差值:0.690735512291113
第1000次遍历整个数据集,当前误差值:0.6852725328458241
第2000次遍历整个数据集,当前误差值:0.6470722240719003
第3000次遍历整个数据集,当前误差值:0.6195245549970402
第4000次遍历整个数据集,当前误差值:0.5765844355950944
第5000次遍历整个数据集,当前误差值:0.6072426395968576
第6000次遍历整个数据集,当前误差值:0.5294033317684576
第7000次遍历整个数据集,当前误差值:0.46076823985930115
第8000次遍历整个数据集,当前误差值:0.465586082399045
第9000次遍历整个数据集,当前误差值:0.4645179722167684
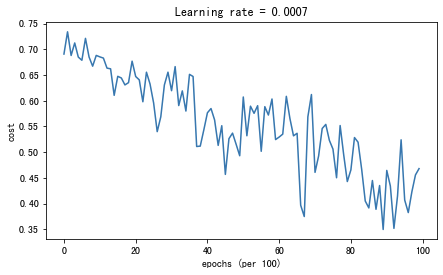
绘制分类的情况:
#预测
preditions = opt_utils.predict(train_X,train_Y,parameters)
#绘制分类图
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5, 2.5])
axes.set_ylim([-1, 1.5])
opt_utils.plot_decision_boundary(lambda x: opt_utils.predict_dec(parameters, x.T), train_X, train_Y)
Accuracy: 0.7966666666666666

Mini-batch gradient descent with momentum
layers_dims = [train_X.shape[0],5,2,1]
#使用动量的梯度下降
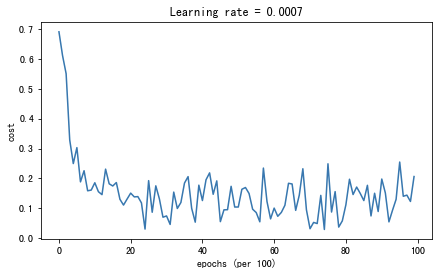
parameters = model(train_X, train_Y, layers_dims, beta=0.9,optimizer="momentum",is_plot=True)
第0次遍历整个数据集,当前误差值:0.6907412988351506
第1000次遍历整个数据集,当前误差值:0.6853405261267578
第2000次遍历整个数据集,当前误差值:0.6471448370095255
第3000次遍历整个数据集,当前误差值:0.6195943032076023
第4000次遍历整个数据集,当前误差值:0.5766650344073023
第5000次遍历整个数据集,当前误差值:0.607323821900647
第6000次遍历整个数据集,当前误差值:0.5294761758786997
第7000次遍历整个数据集,当前误差值:0.46093619004872366
第8000次遍历整个数据集,当前误差值:0.465780093701272
第9000次遍历整个数据集,当前误差值:0.4647395967922748
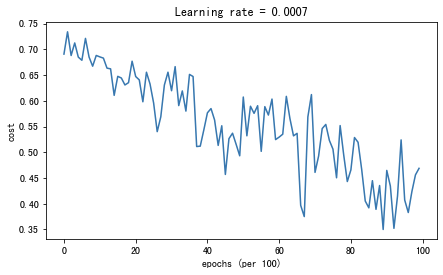
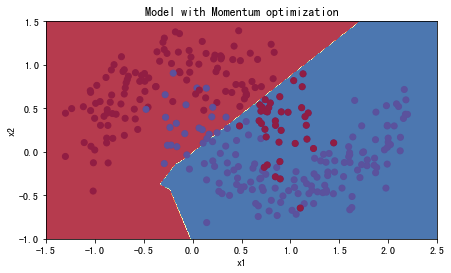
绘制分类的情况:
#预测
preditions = opt_utils.predict(train_X,train_Y,parameters)
#绘制分类图
plt.title("Model with Momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5, 2.5])
axes.set_ylim([-1, 1.5])
opt_utils.plot_decision_boundary(lambda x: opt_utils.predict_dec(parameters, x.T), train_X, train_Y)
Accuracy: 0.7966666666666666
Mini-batch with Adam mode
layers_dims = [train_X.shape[0], 5, 2, 1]
#使用Adam优化的梯度下降
parameters = model(train_X, train_Y, layers_dims, optimizer="adam",is_plot=True)
第0次遍历整个数据集,当前误差值:0.6905522446113365
第1000次遍历整个数据集,当前误差值:0.18550136438550568
第2000次遍历整个数据集,当前误差值:0.15083046575253206
第3000次遍历整个数据集,当前误差值:0.07445438570997176
第4000次遍历整个数据集,当前误差值:0.1259591565133716
第5000次遍历整个数据集,当前误差值:0.10434443534245481
第6000次遍历整个数据集,当前误差值:0.10067637504120656
第7000次遍历整个数据集,当前误差值:0.031652030135115604
第8000次遍历整个数据集,当前误差值:0.111972731312442
第9000次遍历整个数据集,当前误差值:0.19794007152465481
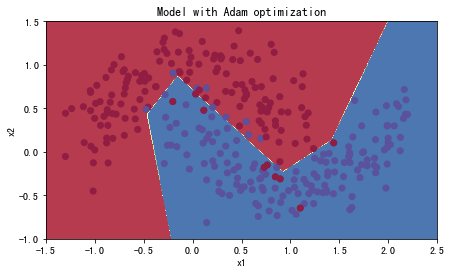
#预测
preditions = opt_utils.predict(train_X,train_Y,parameters)
#绘制分类图
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5, 2.5])
axes.set_ylim([-1, 1.5])
opt_utils.plot_decision_boundary(lambda x: opt_utils.predict_dec(parameters, x.T), train_X, train_Y)
Accuracy: 0.94
Summary

- 具有动量的梯度下降通常可以有很好的效果,但由于小的学习速率和简单的数据集所以它的影响几乎是轻微的。
- Adam明显优于小批量梯度下降和具有动量的梯度下降,如果在这个简单的模型上运行更多时间的数据集,这三种方法都会产生非常好的结果。





