初始化、正则化、梯度检验
任务
一、初始化参数:
- 使用0来初始化参数。
- 使用随机数来初始化参数。
- 使用抑梯度异常初始化参数(参见视频中的梯度消失和梯度爆炸)。
二、正则化模型:
- 使用二范数对二分类模型正则化,尝试避免过拟合。
- 使用随机删除节点的方法精简模型,同样是为了尝试避免过拟合。
三、梯度校验 :
- 对模型使用梯度校验,检测它是否在梯度下降的过程中出现误差过大的情况。
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
import init_utils #第一部分,初始化
import reg_utils #第二部分,正则化
import gc_utils #第三部分,梯度校验
%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
初始化参数
# load image dataset: blue/red dots in circlesb
train_X, train_Y, test_X, test_Y = init_utils.load_dataset()
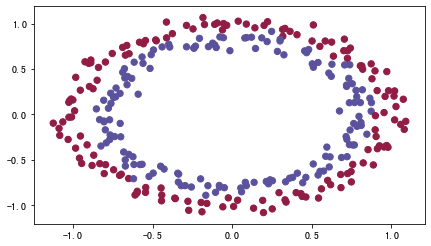
探索学习:
train_X.shape
(2, 300)
train_Y.shape
(1, 300)
# plt.scatter(train_X.T[:, 0], train_X.T[:, 1], c=np.squeeze(train_Y), s=40, cmap=plt.cm.Spectral); # 复现
plt.scatter()
- s:标量或shape大小为(n,)的数组,默认20(好像就是点的大小)
- c:表示的是颜色序列,默认蓝色’b’。c可以是一个RGB或RGBA二维行数组
- cmap = plt.cm.Spectral实现的功能是给label为1的点一种颜色,给label为0的点另一种颜色
- marker:表示的是标记的样式,可选,默认’o’
Neural Network model
尝试三种初始化方法:
- 初始化为0:在输入参数中全部初始化为0
- 初始化为随机数:把输入参数设置为随机值,权重初始化为大的随机值
- 抑梯度异常初始化
def model(X, Y, learning_rate = 0.01, num_iterations = 15000, print_cost = True, initialization = "he", is_polt=True):
"""
Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID.
Arguments:
X -- input data, of shape (2, number of examples)
Y -- true "label" vector (containing 0 for red dots; 1 for blue dots), of shape (1, number of examples)
learning_rate -- learning rate for gradient descent
num_iterations -- number of iterations to run gradient descent
print_cost -- if True, print the cost every 1000 iterations
initialization -- flag to choose which initialization to use ("zeros","random" or "he")
Returns:
parameters -- parameters learnt by the model
"""
grads = {}
costs = [] # to keep track of the loss
m = X.shape[1] # number of examples
layers_dims = [X.shape[0], 10, 5, 1]
# Initialize parameters dictionary.
if initialization == "zeros":
parameters = initialize_parameters_zeros(layers_dims)
elif initialization == "random":
parameters = initialize_parameters_random(layers_dims)
elif initialization == "he":
parameters = initialize_parameters_he(layers_dims)
# Loop (gradient descent)
for i in range(0,num_iterations):
#前向传播
a3 , cache = init_utils.forward_propagation(X,parameters)
#计算成本
cost = init_utils.compute_loss(a3,Y)
#反向传播
grads = init_utils.backward_propagation(X,Y,cache)
#更新参数
parameters = init_utils.update_parameters(parameters,grads,learning_rate)
#记录成本
if i % 1000 == 0:
costs.append(cost)
#打印成本
if print_cost:
print("第" + str(i) + "次迭代,成本值为:" + str(cost))
# plot the loss
if is_polt:
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
Zero initialization
Exercise: Implement the following function to initialize all parameters to zeros.
def initialize_parameters_zeros(layers_dims):
"""
Arguments:
layer_dims -- python array (list) containing the size of each layer.
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
b1 -- bias vector of shape (layers_dims[1], 1)
...
WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
bL -- bias vector of shape (layers_dims[L], 1)
"""
parameters = {}
L = len(layers_dims) # number of layers in the network
for l in range(1, L):
parameters['W' + str(l)] = np.zeros((layers_dims[l], layers_dims[l-1]))
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
return parameters
parameters = initialize_parameters_zeros([3,2,1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
W1 = [[0. 0. 0.]
[0. 0. 0.]]
b1 = [[0.]
[0.]]
W2 = [[0. 0.]]
b2 = [[0.]]
parameters = model(train_X, train_Y, initialization = "zeros")
第0次迭代,成本值为:0.6931471805599453
第1000次迭代,成本值为:0.6931471805599453
第2000次迭代,成本值为:0.6931471805599453
第3000次迭代,成本值为:0.6931471805599453
第4000次迭代,成本值为:0.6931471805599453
第5000次迭代,成本值为:0.6931471805599453
第6000次迭代,成本值为:0.6931471805599453
第7000次迭代,成本值为:0.6931471805599453
第8000次迭代,成本值为:0.6931471805599453
第9000次迭代,成本值为:0.6931471805599453
第10000次迭代,成本值为:0.6931471805599455
第11000次迭代,成本值为:0.6931471805599453
第12000次迭代,成本值为:0.6931471805599453
第13000次迭代,成本值为:0.6931471805599453
第14000次迭代,成本值为:0.6931471805599453

从上图中我们可以看到学习率一直没有变化,也就是说这个模型根本没有学习。我们来看看预测的结果怎么样:
print ("训练集:")
predictions_train = init_utils.predict(train_X, train_Y, parameters)
print ("测试集:")
predictions_test = init_utils.predict(test_X, test_Y, parameters)
训练集:
Accuracy: 0.5
测试集:
Accuracy: 0.5
print("predictions_train = " + str(predictions_train))
print("predictions_test = " + str(predictions_test))
plt.title("Model with Zeros initialization")
axes = plt.gca()
axes.set_xlim([-1.5, 1.5])
axes.set_ylim([-1.5, 1.5])
init_utils.plot_decision_boundary(lambda x: init_utils.predict_dec(parameters, x.T), train_X, train_Y)
predictions_train = [[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0]]
predictions_test = [[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]]
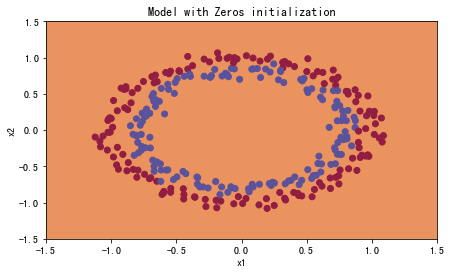
分类失败,该模型预测每个都为0。
通常来说,零初始化都会导致神经网络无法打破对称性,最终导致的结果就是无论网络有多少层,最终只能得到和Logistic函数相同的效果。
Random initialization
def initialize_parameters_random(layers_dims):
"""
Arguments:
layer_dims -- python array (list) containing the size of each layer.
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
b1 -- bias vector of shape (layers_dims[1], 1)
...
WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
bL -- bias vector of shape (layers_dims[L], 1)
"""
np.random.seed(3) # This seed makes sure your "random" numbers will be the as ours
parameters = {}
L = len(layers_dims) # integer representing the number of layers
for l in range(1, L):
### START CODE HERE ### (≈ 2 lines of code)
parameters['W' + str(l)] = np.random.randn(layers_dims[l],layers_dims[l-1])*10
parameters['b' + str(l)] = np.zeros((layers_dims[l],1))
### END CODE HERE ###
return parameters
parameters = initialize_parameters_random([3, 2, 1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
W1 = [[ 17.88628473 4.36509851 0.96497468]
[-18.63492703 -2.77388203 -3.54758979]]
b1 = [[0.]
[0.]]
W2 = [[-0.82741481 -6.27000677]]
b2 = [[0.]]
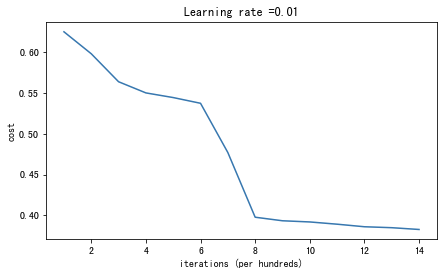
parameters = model(train_X, train_Y, initialization = "random",is_polt=True)
print("训练集:")
predictions_train = init_utils.predict(train_X, train_Y, parameters)
print("测试集:")
predictions_test = init_utils.predict(test_X, test_Y, parameters)
print(predictions_train)
print(predictions_test)
/Users/ldc/Desktop/Project/深度学习wu/init_utils.py:50: RuntimeWarning: divide by zero encountered in log
logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
/Users/ldc/Desktop/Project/深度学习wu/init_utils.py:50: RuntimeWarning: invalid value encountered in multiply
logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
第0次迭代,成本值为:inf
第1000次迭代,成本值为:0.6250676215287511
第2000次迭代,成本值为:0.5981418252875961
第3000次迭代,成本值为:0.563858109377261
第4000次迭代,成本值为:0.5501823050061752
第5000次迭代,成本值为:0.5444756668990652
第6000次迭代,成本值为:0.5374638179631746
第7000次迭代,成本值为:0.4770885368883873
第8000次迭代,成本值为:0.397834663330821
第9000次迭代,成本值为:0.3934832163377203
第10000次迭代,成本值为:0.39203323866307854
第11000次迭代,成本值为:0.3892818629893498
第12000次迭代,成本值为:0.3861521882410713
第13000次迭代,成本值为:0.38499297516135134
第14000次迭代,成本值为:0.38280470097181446
训练集:
Accuracy: 0.83
测试集:
Accuracy: 0.86
[[1 0 1 1 0 0 1 1 1 1 1 0 1 0 0 1 0 1 1 0 0 0 1 0 1 1 1 1 1 1 0 1 1 0 0 1
1 1 1 1 1 1 1 0 1 1 1 1 0 1 0 1 1 1 1 0 0 1 1 1 1 0 1 1 0 1 0 1 1 1 1 0
0 0 0 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1 0 0 1 1 1 0 1 1 0 1 0 1 1 0 1 1 0
1 0 1 1 0 0 1 0 0 1 1 0 1 1 1 0 1 0 0 1 0 1 1 1 1 1 1 1 0 1 1 0 0 1 1 0
0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 0 1 1 0 1 0 1 1 1 1 0 1 1 1
1 0 1 0 1 0 1 1 1 1 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 0 1 1 1 0 1 0 1 0 0 1
0 1 1 0 1 1 0 1 1 0 1 1 1 0 1 1 1 1 0 1 0 0 1 1 0 1 1 1 0 0 0 1 1 0 1 1
1 1 0 1 1 0 1 1 1 0 0 1 0 0 0 1 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 1
1 1 1 1 0 0 0 1 1 1 1 0]]
[[1 1 1 1 0 1 0 1 1 0 1 1 1 0 0 0 0 1 0 1 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 1
0 1 1 0 0 1 1 1 1 1 0 1 1 1 0 1 0 1 1 0 1 0 1 0 1 1 1 1 1 1 1 1 1 0 1 0
1 1 1 1 1 0 1 0 0 1 0 0 0 1 1 0 1 1 0 0 0 1 1 0 1 1 0 0]]
分类效果:
plt.title("Model with large random initialization")
axes = plt.gca()
axes.set_xlim([-1.5, 1.5])
axes.set_ylim([-1.5, 1.5])
init_utils.plot_decision_boundary(lambda x: init_utils.predict_dec(parameters, x.T), train_X, train_Y)
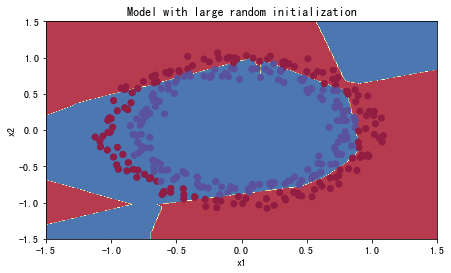
可以看到误差开始很高。这是因为由于具有较大的随机权重,当它出现错误时,它会导致非常高的损失。初始化参数如果没有很好地话会导致梯度消失、爆炸,这也会减慢优化算法。如果我们对这个网络进行更长时间的训练,我们将看到更好的结果,但是使用过大的随机数初始化会减慢优化的速度。
总而言之,将权重初始化为非常大的时候其实效果并不好。
He initialization

def initialize_parameters_he(layers_dims):
"""
Arguments:
layer_dims -- python array (list) containing the size of each layer.
Returns:
parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
b1 -- bias vector of shape (layers_dims[1], 1)
...
WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
bL -- bias vector of shape (layers_dims[L], 1)
"""
np.random.seed(3) # 指定随机种子
parameters = {}
L = len(layers_dims) # 层数
for l in range(1, L):
parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * np.sqrt(2 / layers_dims[l - 1])
parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
#使用断言确保我的数据格式是正确的
assert(parameters["W" + str(l)].shape == (layers_dims[l],layers_dims[l-1]))
assert(parameters["b" + str(l)].shape == (layers_dims[l],1))
return parameters
parameters = initialize_parameters_he([2, 4, 1])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
W1 = [[ 1.78862847 0.43650985]
[ 0.09649747 -1.8634927 ]
[-0.2773882 -0.35475898]
[-0.08274148 -0.62700068]]
b1 = [[0.]
[0.]
[0.]
[0.]]
W2 = [[-0.03098412 -0.33744411 -0.92904268 0.62552248]]
b2 = [[0.]]
parameters = model(train_X, train_Y, initialization = "he",is_polt=True)
print("训练集:")
predictions_train = init_utils.predict(train_X, train_Y, parameters)
print("测试集:")
init_utils.predictions_test = init_utils.predict(test_X, test_Y, parameters)
第0次迭代,成本值为:0.8830537463419761
第1000次迭代,成本值为:0.6879825919728063
第2000次迭代,成本值为:0.6751286264523371
第3000次迭代,成本值为:0.6526117768893807
第4000次迭代,成本值为:0.6082958970572938
第5000次迭代,成本值为:0.5304944491717495
第6000次迭代,成本值为:0.4138645817071794
第7000次迭代,成本值为:0.3117803464844441
第8000次迭代,成本值为:0.23696215330322556
第9000次迭代,成本值为:0.18597287209206836
第10000次迭代,成本值为:0.15015556280371817
第11000次迭代,成本值为:0.12325079292273551
第12000次迭代,成本值为:0.09917746546525935
第13000次迭代,成本值为:0.08457055954024278
第14000次迭代,成本值为:0.07357895962677366
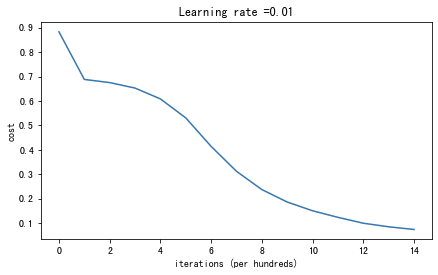
训练集:
Accuracy: 0.9933333333333333
测试集:
Accuracy: 0.96
plt.title("Model with He initialization")
axes = plt.gca()
axes.set_xlim([-1.5, 1.5])
axes.set_ylim([-1.5, 1.5])
init_utils.plot_decision_boundary(lambda x: init_utils.predict_dec(parameters, x.T), train_X, train_Y)

总结:
- 不同的初始化方法可能导致性能最终不同
- 随机初始化有助于打破对称,使得不同隐藏层的单元可以学习到不同的参数
- 初始化时,初始值不宜过大
- He初始化搭配ReLU激活函数常常可以得到不错的效果
Regularization
要做以下三件事,来对比出不同的模型的优劣:
不使用正则化
使用正则化
- 使用L2正则化
- 使用随机节点删除
train_X, train_Y, test_X, test_Y = reg_utils.load_2D_dataset(is_plot=True)
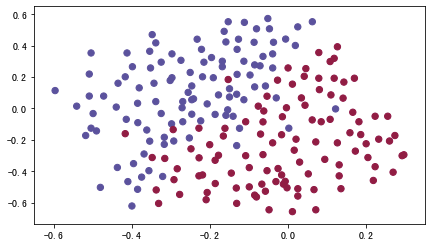
每一个点代表球落下的可能的位置,蓝色代表己方的球员会抢到球,红色代表对手的球员会抢到球,我们要做的就是使用模型来画出一条线,来找到适合我方球员能抢到球的位置。
def model(X,Y,learning_rate=0.3,num_iterations=30000,print_cost=True,is_plot=True,lambd=0,keep_prob=1):
"""
实现一个三层的神经网络:LINEAR ->RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
参数:
X - 输入的数据,维度为(2, 要训练/测试的数量)
Y - 标签,【0(蓝色) | 1(红色)】,维度为(1,对应的是输入的数据的标签)
learning_rate - 学习速率
num_iterations - 迭代的次数
print_cost - 是否打印成本值,每迭代10000次打印一次,但是每1000次记录一个成本值
is_polt - 是否绘制梯度下降的曲线图
lambd - 正则化的超参数,实数
keep_prob - 随机删除节点的概率
返回
parameters - 学习后的参数
"""
grads = {}
costs = []
m = X.shape[1]
layers_dims = [X.shape[0],20,3,1]
#初始化参数
parameters = reg_utils.initialize_parameters(layers_dims)
#开始学习
for i in range(0,num_iterations):
#前向传播
##是否随机删除节点
if keep_prob == 1:
###不随机删除节点
a3 , cache = reg_utils.forward_propagation(X,parameters)
elif keep_prob < 1:
###随机删除节点
a3 , cache = forward_propagation_with_dropout(X,parameters,keep_prob)
else:
print("keep_prob参数错误!程序退出。")
exit
#计算成本
## 是否使用二范数
if lambd == 0:
###不使用L2正则化
cost = reg_utils.compute_cost(a3,Y)
else:
###使用L2正则化
cost = compute_cost_with_regularization(a3,Y,parameters,lambd)
#反向传播
##可以同时使用L2正则化和随机删除节点,但是本次实验不同时使用。
assert(lambd == 0 or keep_prob ==1)
##两个参数的使用情况
if (lambd == 0 and keep_prob == 1):
### 不使用L2正则化和不使用随机删除节点
grads = reg_utils.backward_propagation(X,Y,cache)
elif lambd != 0:
### 使用L2正则化,不使用随机删除节点
grads = backward_propagation_with_regularization(X, Y, cache, lambd)
elif keep_prob < 1:
### 使用随机删除节点,不使用L2正则化
grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)
#更新参数
parameters = reg_utils.update_parameters(parameters, grads, learning_rate)
#记录并打印成本
if i % 1000 == 0:
## 记录成本
costs.append(cost)
if (print_cost and i % 10000 == 0):
#打印成本
print("第" + str(i) + "次迭代,成本值为:" + str(cost))
#是否绘制成本曲线图
if is_plot:
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (x1,000)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
#返回学习后的参数
return parameters
Non-regularized
parameters = model(train_X, train_Y,is_plot=True)
print("训练集:")
predictions_train = reg_utils.predict(train_X, train_Y, parameters)
print("测试集:")
predictions_test = reg_utils.predict(test_X, test_Y, parameters)
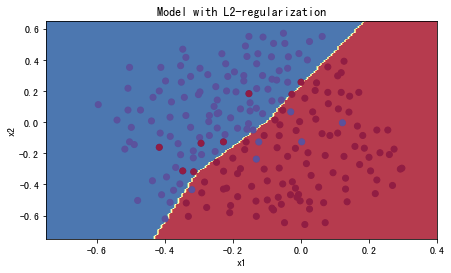
第0次迭代,成本值为:0.6557412523481002
第10000次迭代,成本值为:0.16329987525724213
第20000次迭代,成本值为:0.1385164242325368
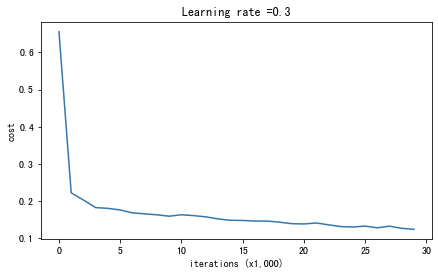
训练集:
Accuracy: 0.9478672985781991
测试集:
Accuracy: 0.915
plt.title("Model without regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
reg_utils.plot_decision_boundary(lambda x: reg_utils.predict_dec(parameters, x.T), train_X, train_Y)
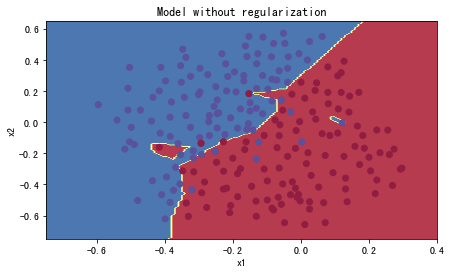
在无正则化时,分割曲线有了明显的过拟合特性
L2 Regularization
The standard way to avoid overfitting is called L2 regularization. It consists of appropriately modifying your cost function.
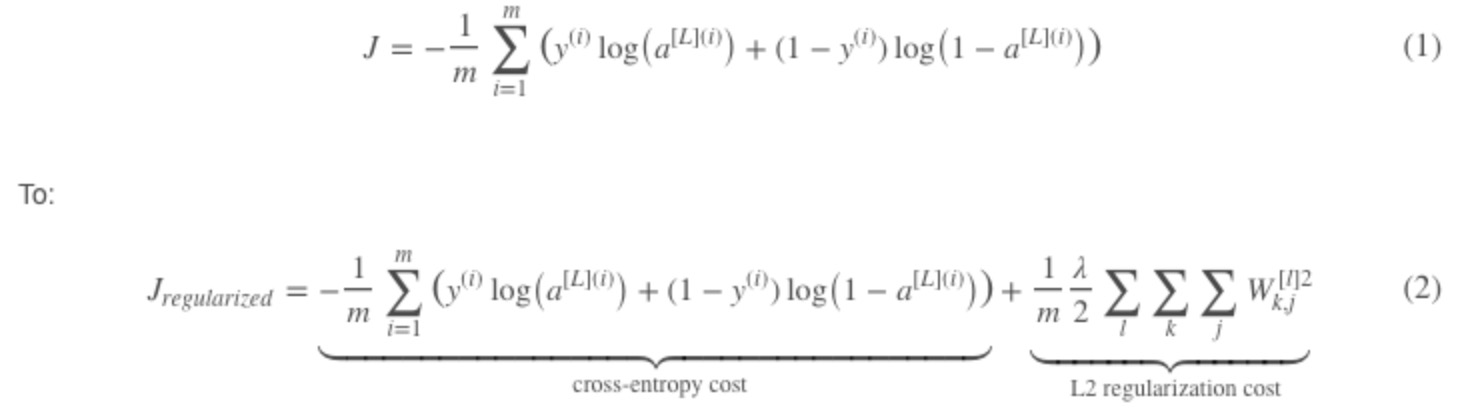
To calculate L2 regularization cost , use :
np.sum(np.square(Wl))
def compute_cost_with_regularization(A3, Y, parameters, lambd):
"""
Implement the cost function with L2 regularization. See formula (2) above.
Arguments:
A3 -- post-activation, output of forward propagation, of shape (output size, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
parameters -- python dictionary containing parameters of the model
Returns:
cost - value of the regularized loss function (formula (2))
"""
m = Y.shape[1]
W1 = parameters["W1"]
W2 = parameters["W2"]
W3 = parameters["W3"]
cross_entropy_cost = reg_utils.compute_cost(A3,Y)
L2_regularization_cost = lambd * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3))) / (2 * m)
cost = cross_entropy_cost + L2_regularization_cost
return cost
def backward_propagation_with_regularization(X, Y, cache, lambd):
"""
Implements the backward propagation of our baseline model to which we added an L2 regularization.
Arguments:
X -- input dataset, of shape (input size, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
cache -- cache output from forward_propagation()
lambd -- regularization hyperparameter, scalar
Returns:
gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = (1 / m) * np.dot(dZ3,A2.T) + ((lambd * W3) / m )
db3 = (1 / m) * np.sum(dZ3,axis=1,keepdims=True)
dA2 = np.dot(W3.T,dZ3)
dZ2 = np.multiply(dA2,np.int64(A2 > 0))
dW2 = (1 / m) * np.dot(dZ2,A1.T) + ((lambd * W2) / m)
db2 = (1 / m) * np.sum(dZ2,axis=1,keepdims=True)
dA1 = np.dot(W2.T,dZ2)
dZ1 = np.multiply(dA1,np.int64(A1 > 0))
dW1 = (1 / m) * np.dot(dZ1,X.T) + ((lambd * W1) / m)
db1 = (1 / m) * np.sum(dZ1,axis=1,keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
parameters = model(train_X, train_Y, lambd=0.7,is_plot=True)
print("使用正则化,训练集:")
predictions_train = reg_utils.predict(train_X, train_Y, parameters)
print("使用正则化,测试集:")
predictions_test = reg_utils.predict(test_X, test_Y, parameters)
第0次迭代,成本值为:0.6974484493131264
第10000次迭代,成本值为:0.2684918873282239
第20000次迭代,成本值为:0.26809163371273004

使用正则化,训练集:
Accuracy: 0.9383886255924171
使用正则化,测试集:
Accuracy: 0.93
plt.title("Model with L2-regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
reg_utils.plot_decision_boundary(lambda x: reg_utils.predict_dec(parameters, x.T), train_X, train_Y)
L2正则化对以下内容有影响:
- 成本计算:正则化的计算需要添加到成本函数中
- 反向传播:在权重矩阵方面,梯度计算时也要依据正则化来做出相应的计算
- 重量变小(“重量衰减”):权重被逐渐改变到较小的值
Dropout
Dropout的原理就是每次迭代过程中随机将其中的一些节点失效。当我们关闭一些节点时,我们实际上修改了我们的模型。背后的想法是,在每次迭代时,我们都会训练一个只使用一部分神经元的不同模型。随着迭代次数的增加,我们的模型的节点会对其他特定节点的激活变得不那么敏感,因为其他节点可能在任何时候会失效。

def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):
"""
Implements the forward propagation: LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.
Arguments:
X -- input dataset, of shape (2, number of examples)
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
W1 -- weight matrix of shape (20, 2)
b1 -- bias vector of shape (20, 1)
W2 -- weight matrix of shape (3, 20)
b2 -- bias vector of shape (3, 1)
W3 -- weight matrix of shape (1, 3)
b3 -- bias vector of shape (1, 1)
keep_prob - probability of keeping a neuron active during drop-out, scalar
Returns:
A3 -- last activation value, output of the forward propagation, of shape (1,1)
cache -- tuple, information stored for computing the backward propagation
"""
np.random.seed(1)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
#LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1,X) + b1
A1 = reg_utils.relu(Z1)
#下面的步骤1-4对应于上述的步骤1-4。
D1 = np.random.rand(A1.shape[0],A1.shape[1]) #步骤1:初始化矩阵D1 = np.random.rand(..., ...)
D1 = D1 < keep_prob #步骤2:将D1的值转换为0或1(使用keep_prob作为阈值)
A1 = A1 * D1 #步骤3:舍弃A1的一些节点(将它的值变为0或False)
A1 = A1 / keep_prob #步骤4:缩放未舍弃的节点(不为0)的值
Z2 = np.dot(W2,A1) + b2
A2 = reg_utils.relu(Z2)
#下面的步骤1-4对应于上述的步骤1-4。
D2 = np.random.rand(A2.shape[0],A2.shape[1]) #步骤1:初始化矩阵D2 = np.random.rand(..., ...)
D2 = D2 < keep_prob #步骤2:将D2的值转换为0或1(使用keep_prob作为阈值)
A2 = A2 * D2 #步骤3:舍弃A1的一些节点(将它的值变为0或False)
A2 = A2 / keep_prob #步骤4:缩放未舍弃的节点(不为0)的值
Z3 = np.dot(W3, A2) + b3
A3 = reg_utils.sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cache
改变了前向传播的算法,也需要改变后向传播的算法,使用存储在缓存中的舍弃节点信息添加到第一个和第二个隐藏层:
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
"""
Implements the backward propagation of our baseline model to which we added dropout.
Arguments:
X -- input dataset, of shape (2, number of examples)
Y -- "true" labels vector, of shape (output size, number of examples)
cache -- cache output from forward_propagation_with_dropout()
keep_prob - probability of keeping a neuron active during drop-out, scalar
Returns:
gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables
"""
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = (1 / m) * np.dot(dZ3,A2.T)
db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dA2 = dA2 * D2 # 步骤1:使用正向传播期间相同的节点,舍弃那些关闭的节点(因为任何数乘以0或者False都为0或者False)
dA2 = dA2 / keep_prob # 步骤2:缩放未舍弃的节点(不为0)的值
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1. / m * np.dot(dZ2, A1.T)
db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dA1 = dA1 * D1 # 步骤1:使用正向传播期间相同的节点,舍弃那些关闭的节点(因为任何数乘以0或者False都为0或者False)
dA1 = dA1 / keep_prob # 步骤2:缩放未舍弃的节点(不为0)的值
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1. / m * np.dot(dZ1, X.T)
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
parameters = model(train_X, train_Y, keep_prob=0.86, learning_rate=0.3,is_plot=True)
print("使用随机删除节点,训练集:")
predictions_train = reg_utils.predict(train_X, train_Y, parameters)
print("使用随机删除节点,测试集:")
reg_utils.predictions_test = reg_utils.predict(test_X, test_Y, parameters)
第0次迭代,成本值为:0.6543912405149825
/Users/ldc/Desktop/Project/深度学习wu/reg_utils.py:121: RuntimeWarning: divide by zero encountered in log
logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
/Users/ldc/Desktop/Project/深度学习wu/reg_utils.py:121: RuntimeWarning: invalid value encountered in multiply
logprobs = np.multiply(-np.log(a3),Y) + np.multiply(-np.log(1 - a3), 1 - Y)
第10000次迭代,成本值为:0.061016986574905605
第20000次迭代,成本值为:0.060582435798513114
使用随机删除节点,训练集:
Accuracy: 0.9289099526066351
使用随机删除节点,测试集:
Accuracy: 0.95
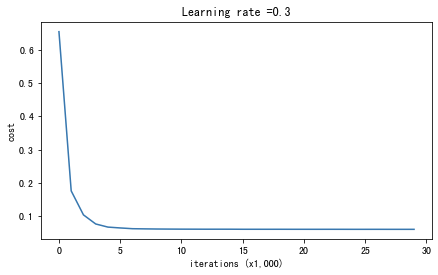
plt.title("Model with dropout")
axes = plt.gca()
axes.set_xlim([-0.75, 0.40])
axes.set_ylim([-0.75, 0.65])
reg_utils.plot_decision_boundary(lambda x: reg_utils.predict_dec(parameters, x.T), train_X, train_Y)
正则化会把训练集的准确度降低,但是测试集的准确度提高了
结论
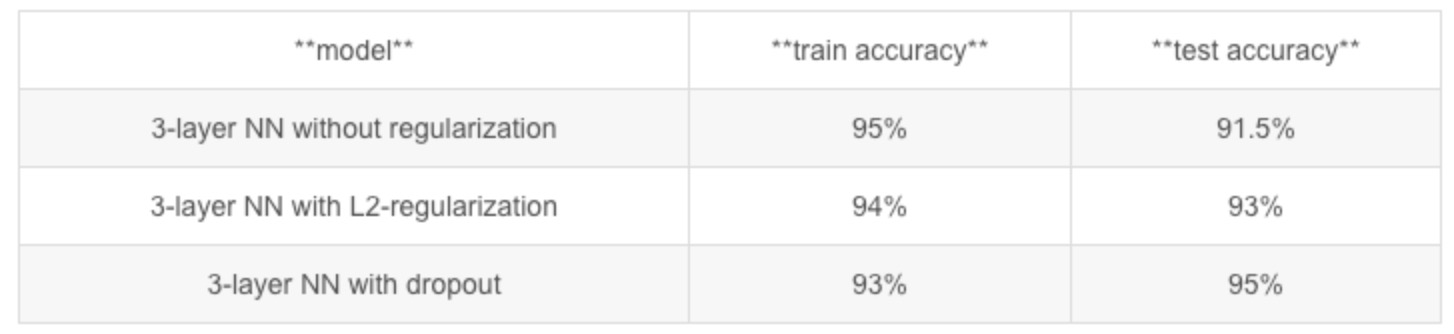
- Regularization will help you reduce overfitting.
- Regularization will drive your weights to lower values.
- L2 regularization and Dropout are two very effective regularization techniques.
Gradient Checking
一维线性模型的梯度检查计算过程:

1-dimensional gradient checking
Exercise: implement “forward propagation” and “backward propagation” for this simple function.
def forward_propagation(x, theta):
"""
Implement the linear forward propagation (compute J) presented in Figure 1 (J(theta) = theta * x)
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
Returns:
J -- the value of function J, computed using the formula J(theta) = theta * x
"""
J = np.dot(theta, x)
return J
x, theta = 2, 4
J = forward_propagation(x, theta)
print ("J = " + str(J))
J = 8
def backward_propagation(x, theta):
"""
Computes the derivative of J with respect to theta (see Figure 1).
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
Returns:
dtheta -- the gradient of the cost with respect to theta
"""
dtheta = x
return dtheta
x, theta = 2, 4
dtheta = backward_propagation(x, theta)
print ("dtheta = " + str(dtheta))
dtheta = 2
梯度检查

def gradient_check(x, theta, epsilon = 1e-7):
"""
Implement the backward propagation presented in Figure 1.
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
Returns:
difference -- difference (2) between the approximated gradient and the backward propagation gradient
"""
thetaplus = theta + epsilon
thetaminus = theta - epsilon
J_plus = forward_propagation(x, thetaplus)
J_minus = forward_propagation(x, thetaminus)
gradapprox = (J_plus - J_minus) / (2 * epsilon)
grad = backward_propagation(x, theta)
# numpy.linalg模块包含线性代数的函数。使用这个模块,可以计算逆矩阵、求特征值、解线性方程组以及求解行列式等
numerator = np.linalg.norm(grad - gradapprox)
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)
difference = numerator / denominator
if difference < 1e-7:
print ("The gradient is correct!")
else:
print ("The gradient is wrong!")
return difference
x, theta = 2, 4
difference = gradient_check(x, theta)
print("difference = " + str(difference))
The gradient is correct!
difference = 2.919335883291695e-10
N-dimensional gradient checking
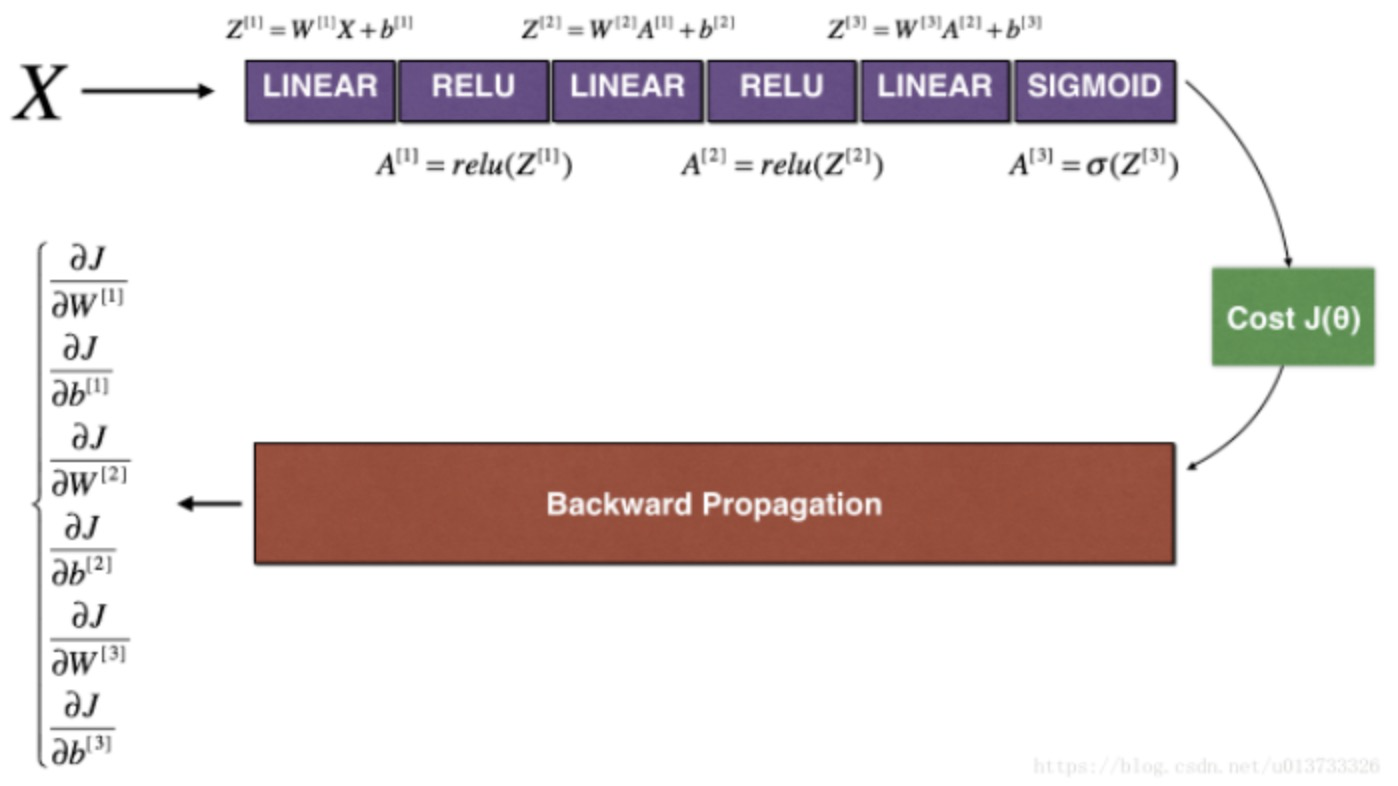
def forward_propagation_n(X, Y, parameters):
"""
Implements the forward propagation (and computes the cost) presented in Figure 3.
Arguments:
X -- training set for m examples
Y -- labels for m examples
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
W1 -- weight matrix of shape (5, 4)
b1 -- bias vector of shape (5, 1)
W2 -- weight matrix of shape (3, 5)
b2 -- bias vector of shape (3, 1)
W3 -- weight matrix of shape (1, 3)
b3 -- bias vector of shape (1, 1)
Returns:
cost -- the cost function (logistic cost for one example)
"""
# retrieve parameters
m = X.shape[1]
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
# Cost
logprobs = np.multiply(-np.log(A3),Y) + np.multiply(-np.log(1 - A3), 1 - Y)
cost = 1./m * np.sum(logprobs)
cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3)
return cost, cache
def backward_propagation_n(X, Y, cache):
"""
Implement the backward propagation presented in figure 2.
Arguments:
X -- input datapoint, of shape (input size, 1)
Y -- true "label"
cache -- cache output from forward_propagation_n()
Returns:
gradients -- A dictionary with the gradients of the cost with respect to each parameter, activation and pre-activation variables.
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T)
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,
"dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2,
"dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
def gradient_check_n(parameters,gradients,X,Y,epsilon=1e-7):
"""
检查backward_propagation_n是否正确计算forward_propagation_n输出的成本梯度
参数:
parameters - 包含参数“W1”,“b1”,“W2”,“b2”,“W3”,“b3”的python字典:
grad_output_propagation_n的输出包含与参数相关的成本梯度。
x - 输入数据点,维度为(输入节点数量,1)
y - 标签
epsilon - 计算输入的微小偏移以计算近似梯度
返回:
difference - 近似梯度和后向传播梯度之间的差异
"""
#初始化参数
parameters_values , keys = gc_utils.dictionary_to_vector(parameters) #keys用不到
grad = gc_utils.gradients_to_vector(gradients)
num_parameters = parameters_values.shape[0]
J_plus = np.zeros((num_parameters,1))
J_minus = np.zeros((num_parameters,1))
gradapprox = np.zeros((num_parameters,1))
#计算gradapprox
for i in range(num_parameters):
#计算J_plus [i]。输入:“parameters_values,epsilon”。输出=“J_plus [i]”
thetaplus = np.copy(parameters_values) # Step 1
thetaplus[i][0] = thetaplus[i][0] + epsilon # Step 2
J_plus[i], cache = forward_propagation_n(X,Y,gc_utils.vector_to_dictionary(thetaplus)) # Step 3 ,cache用不到
#计算J_minus [i]。输入:“parameters_values,epsilon”。输出=“J_minus [i]”。
thetaminus = np.copy(parameters_values) # Step 1
thetaminus[i][0] = thetaminus[i][0] - epsilon # Step 2
J_minus[i], cache = forward_propagation_n(X,Y,gc_utils.vector_to_dictionary(thetaminus))# Step 3 ,cache用不到
#计算gradapprox[i]
gradapprox[i] = (J_plus[i] - J_minus[i]) / (2 * epsilon)
#通过计算差异比较gradapprox和后向传播梯度。
numerator = np.linalg.norm(grad - gradapprox) # Step 1'
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox) # Step 2'
difference = numerator / denominator # Step 3'
if difference < 1e-7:
print("梯度检查:梯度正常!")
else:
print("梯度检查:梯度超出阈值!")
return difference





