[辐射基础] 必须要弄懂系列之 (1) 基本辐射度量
关键词：辐射度量 传感器 地物
作者：李二
日期：4/11/2020 - 5/11/2020
2020.11.9:更正辐照度公式的错误
一直以来，包括我在内，很多遥感圈内的人对于基本的辐射度量(radiometric quantities)以及反射度量(reflectance quantities)的概念，并不是很清楚，或者仅仅浮于表面，稍微一往深里问，就凌乱了。
因为最近手头有篇文章在修改，同时也阅读了一些相关文献，发现多篇已发表的文献中竟然有诸多错误，我觉得有必要整理一下这些基本概念，供自己和其他朋友参考。
0. 前言
在定量遥感中，好多人可能会碰到如下疑问（包括但不限于）：
入射辐射量用 辐射通量表示还是用辐照度抑或辐亮度表示比较合适？传感器接收到的物理量到底是什么？ 辐射通量还是辐亮度？为什么总看到某个 辐射量要乘以，什么时候要乘，什么时候不用乘？反射率怎么体现出是一个方向相关的量？反射率到底怎么算？反射率能否大于1？反射率和反照率有什么区别？反射因子可否大于1？它和反射率有什么区别？为什么在 二向性反射分布函数(BRDF)的表征中，二向性反射因子（或方向-方向反射因子）中叫反射因子，而方向-半球反射率中叫反射率？
相信这些问题很容易把大家问懵。在这个系列中，我将逐步理清各个概念，同时解释上述的这些问题，并且探讨几个有趣的小例子。
注意：我将尽全力保证后面的博文是理论正确的，但难免有自己的理解偏颇，敬请大佬批评指正。
1. 从传感器开始讲起
我觉得吧，基本所有的
遥感和辐射度学书籍一上来就直接介绍各种各样的辐射度量和立体角(solid angle)的方式是很不友好的。直接塞给读者这样的知识，而非启发性的教学，或者并没有和实际应用中的一些东西联系起来，导致读者很容易不知所以和不明就里。
既然我们是遥感圈内人，必然离不开各种各样的传感器(detector/sensor)用以“遥远"的感知，我觉得从传感器开始讲起是更容易接受的。
首先想第一个问题：传感器接收到的物理量到底是什么？
毫无疑问，最简单的回答当然的
光能，而能量的单位当然是焦耳(Joule, J)。我们都知道，传感器(例如CCD或者CMOS)是接收光能后发生光电效应(Photoelectric Effect)，从而产生电信号被记录下来，最终每个像元或者sensor element得到一个数值(digital number)。这里我们暂且不考虑传感器的
响应度(即光信号转换为电信号的能力)等传感器自身的参数。最终，我们可以认为传感器接收到的物理量是
辐射能量(radiant energy)，用符号表示。
2. 地物辐射的真实状况
我们再想第二个问题：辐射能量能否准确地反映地物辐射的真实情况？
想象有两个不同的传感器，各自的
积分时间(integration time)不同 (普通相机可以称为曝光时间(exposure time)，星载传感器的积分时间是固定的，普通相机的可以自行设置)。积分时间(或感光时间)长的传感器自然接收的能量多，感光时间短的自然接收的能力就少。这说明
辐射能量不仅与地物辐射有关，而且与传感器参数有关。因此其并不能准确反映地物的真实辐射状况。
那我们立刻就想到了，我们用
单位时间的辐射能量(单位J/s或W)来描述，不就避免了传感器之间积分时间不一致的问题了么，这时我们有了一个新的辐射度量--辐射通量(radiant flux, Φ)。很棒！但是再想一下，不同传感器之间，sensor element（或者像元）的
物理尺寸(physical size)可能并不一样，有的大而有的小。尺寸大的像元必然接收的辐射通量多呀。这说明
辐射通量依然与传感器参数有关，因此也不能准确反映地物的真实辐射状况。
这里额外说一句，许多传感器的响应值并不取决于辐射能量的时间累积值，而是取决于辐射通量的大小.
自然地，我们可以用
单位面积内的辐射通量(单位W/m2)来描述，就避免了传感器尺寸大小的差异，因此命名该物理量为辐照度(irradiance, E)。哈哈，又进了一步！这难道就可以了吗？似乎依然不是，想象两个传感器的积分时间和像元尺寸完全相同，但是
视场角(field of view,FOV)不同，那么大视场角对应的地面范围肯定更大，传感器接收的辐照度通常也会更大。这说明
辐照度依然与传感器参数有关，因此也不能准确反映地物的真实辐射状况。
于是，我们尝试在单位空间角度中定义一个新的物理量，来避免视场角差异的问题。由于是在三维空间中定义角度，我们引入
立体角(solid angle, Ω,单位为球面度(steradian,sr))的概念（稍后再细讲）。于是用单位面积单位立体角内的辐射通量(单位:W/m2/sr)来描述，命名为辐亮度(radiance, L)。终于成功了。这里的
单位面积指的是垂直于光线的，至于为什么要用垂直于光线的平面，我们以后再说。应该来讲，这个
辐亮度应该不再与传感器的参数相关了。这说明
辐亮度能够准确反映地物的真实辐射状况。
3. 如果以地物为参照呢？
刚刚我们
以传感器为研究对象，介绍了一些常用辐射度量的由来。其实，我们也可以以地物为研究对象，也对应介绍一下这些辐射度量。
成像学科中有时习惯以传感器为研究对象，而辐射度学科中习惯以地物(或光源，)为研究对象。
既然我们想了解地物的真实辐射情况，那不妨先去除传感器，直接看地物是如何辐射的就好了。
此时，我们假定地物是光源（其实地物就是光源，无非是二次光源而已）。下面博文中写到地物时，就默认它就是光源，那么地物的反射可以视为发射了。
地物以辐射的形式发射能量，叫做
辐射能量(radiant energy, 单位：焦耳(Joule, J))。为了进一步描述辐射能量随时间、空间、方向等分布的特点，我们引出以下几个辐射度量。
辐射通量(radiant flux, Φ): 描述了辐射能的时间特性，定义为单位时间内的辐射能量。
这里我个人建议，以辐射通量为基础进行许多公式的推导，则不容易被辐射的方向性问题所弄糊涂。
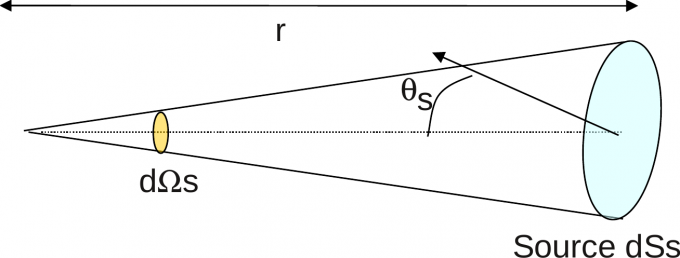
辐射强度(radiant intensity, I): 描述辐射通量的方向特性。因为通常地物(想象一个小的辐射面元)向各个方向辐射的辐射通量并不相同，所以采用辐射强度来描述方向性特征。我们采用微分
立体角(对应于一个极小的圆锥)来表示方向(directional)。因此我们定义其为单位立体角内的辐射通量。这里的单位立体角并非指的是数值
1 sr，而是某个给定传输方向上的微分立体角元。
这里很容易想到，为什么有了
辐亮度已然能够描述方向性了，还要单独定义辐射强度？假如有一个点光源，在某个给定方向上的微分立体角内，如果在传输介质中没有任何任何散射与吸收，那么不论辐射传输距离有多远，其辐射通量是不变的。而如果采用辐亮度的话，则与接收截面的面积有关。
辐照度(irradiance, E): 描述微分面元接收到的辐射通量。我们沿用第2部分的公式：注意这里并
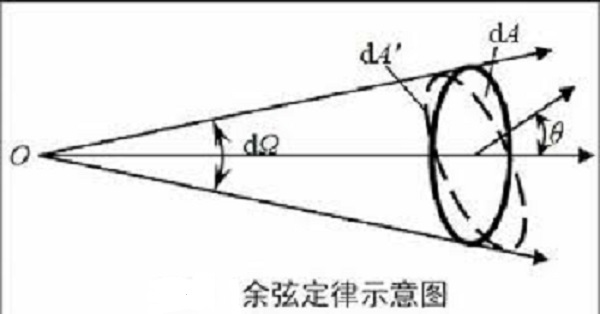
没有说微分面元是否垂直于辐射光线反方向。关于辐照度，一个常用的定律是
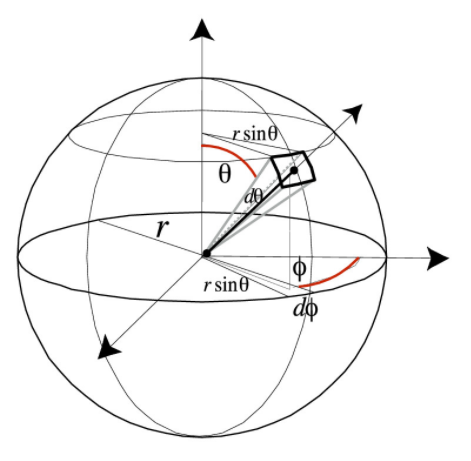
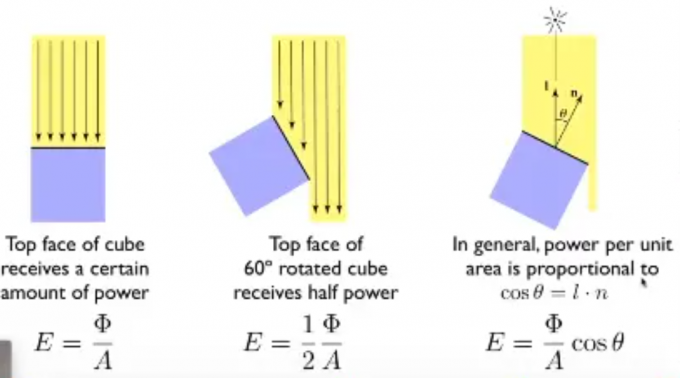
朗伯余弦定律，我们也顺便讲一下。由下图所示，在立体角内，有
垂直于传输方向上的面元和与传输方向成角的面元。前面已经提到，同一立体角内的辐射通量不随传输距离的变化而变化。那么面元和面元的辐照度和分别为：; 其中 所以有
这就是辐照度的
朗伯余弦定律。 这对于任意光线（如平行光）都是适用的。可以想象，如果微分面元平行于光线，则根本接收不到任何辐射能量。
辐照度这里还有一个平方反比定律，但是遥感中用的不多，虽然也很简单，但是不讲了。
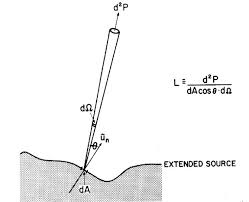
辐亮度(radiance, L): 描述了微分面元在垂直辐射传输方向上辐射强度特性。地物在垂直其辐射传输方向上单位面积单位立体角内的辐射通量。
注意该
微分面元指的是垂直于光线方向的微分面元，至于为什么要垂直于光线方向，我后面补充吧。通常，辐亮度描述
面光源很合适（诸如地物，天空），辐射强度描述点光源更为合适。但是一个微分面元也可以视为点光源。实际中，在描述天空光辐射特性时，往往采用辐亮度的概念。辐亮度这个概念在光辐射能的传输和测量中起到核心作用。
总结一下，不同辐射度量之间的关系如下：
4. 再说立体角
前面已经多次提到了立体角的概念，其实这个概念是许多书本中开篇就要提到的。我把它放到最后是因为它并不影响前面的表述。
我们前面一直采用的是微分立体角元，主要是想用其代表某一方向。
当然，如果立体角的数值本身较大时，则不能描述单一方向了，应该是描述多个方向，或者说多个方向的积分。
立体角 (soild angle):描述辐射能向空间发射、传输、或被某一表面接收时的发散或会聚的角度。计算方法是：以椎体的顶点为球心做一球表面，该椎体在球表面上所截取部分的表面积和球半径平方的比，单位为球面度 steradian (sr)。
自然地，整个球的立体角是 ，半球的立体角为。天空光对于地物微分面元的辐亮度就来自空间，地物微分面元的反射通常也是向空间辐射。
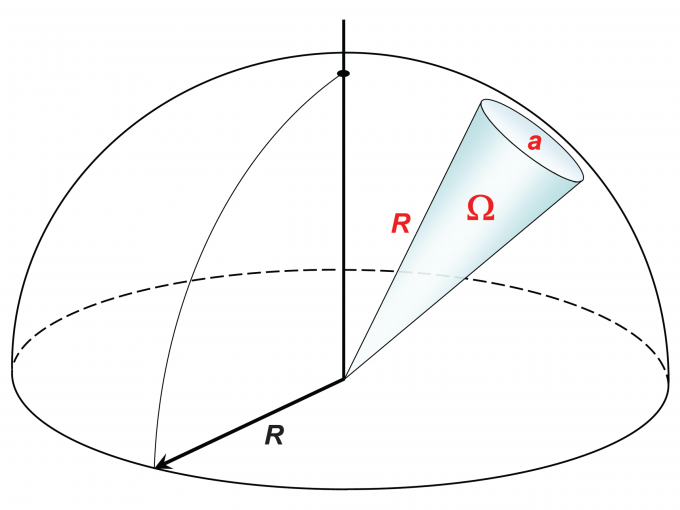
我们往往关注的是某一方向，以及如何由多个方向积分得到一个大立体角内的辐射通量。而我们在三维空间中通常采用天顶角和方位角一起表示某一个方向，这样计算也更为方便。因此要建立与和的关系：
因此在和角度范围内（多个方向，对应较大立体角）的立体角计算公式为：
强调一下，不管空间表面的凹凸如何，只要他们对同一点作射线束围成的空间角是相同的，那么它们就有相同的立体角。
5. 结语
这期博文我们讲解了几个常用的辐射度量，他们是辐射度学、光度学、遥感科学的基础知识，一定要掌握。
既然我们创建各种辐射度量的目的是为了描述地物的辐射状况，那么我们下一期就以一些地物为例，展示其各自的辐射特点。诸如：
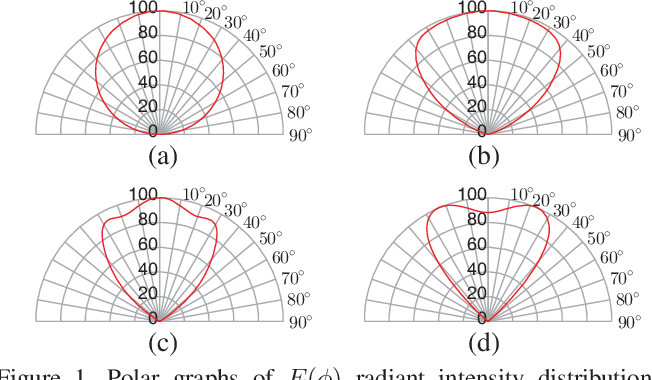
朗伯 Lambertian表面(或称为各向同性 isotropic表面)非朗伯 Non-Lambertian表面(或称为各向异性 anisotropic表面)特殊地，还有 镜 specular面
如有错误，敬请及时指正，以免误导他人！
