[二维成像与三维重建]系列(4) 小心成像有畸变
关键词：影像畸变 径向畸变 切向畸变 畸变模型
作者：李二
日期：28/03/2020 - 01/04/2020
"本系列均是写给计算机视觉和摄影测量的初学者和非主流从业人员，比如一些遥感研究生们。"
小孔成像模型的
数学形式是完美的，然而真实的相机成像过程并非严格遵从小孔成像模型，这一期我们来看看真实的薄透镜成像有什么问题，在成像几何中如何考虑。话不多说，看李二道来。
1. 理想相机成像
理想相机成像即严格遵循小孔成像模型：无镜头，无畸变
李二再一次来到了**吃饭大学，开始了他的兼职教授的第二次课程。我当然是紧随其后，以便中午能蹭顿便饭，因为听说该大学西北餐厅的手抓羊肉一绝呀。
李二开始上课：上回说到，唐王被困淤泥河，薛仁贵前去救驾.... （致敬刘宝瑞先生）
第三排第末列的女孩突然打断：二先生，你走错了吧，这不是茶馆。
李二恍然大悟：奥奥奥，对对对，昨天晚上睡不着，听了一夜相声。好，上节课我们留了个扣子，我说真实相机成像
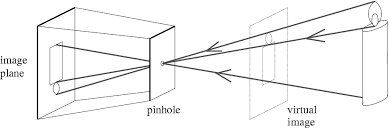
并非完美地严格地遵从小孔成像模型，那么不妨先看看这种理想的小孔成像模型到底理想在什么地方呢。如下图所示：所谓
理想主要体现在两个方面：
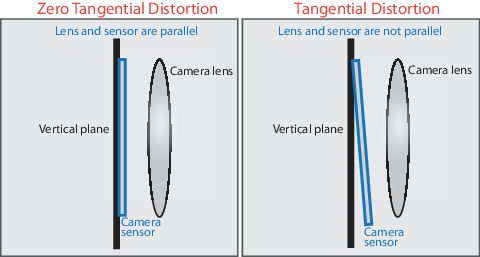
成像平面与焦平面(即小孔所在平面)严格平行； 像点与物点的连线(即光线或)严格准直，不存在弯曲； 大家记住理想成像的这两个
特点，然后我们看看真实相机成像是什么样的。
2. 真实相机成像的问题 - 畸变
真实相机的几何构造与理想情况有差异：有镜头，有畸变
真实相机因为
制造工艺的原因，它的几何构造与理想情况有差异，涉及两个方面：
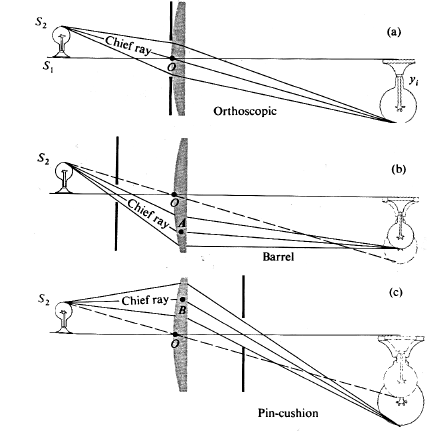
透镜与孔径光阑的相对位置：本质上是 孔径光阑和镜片位置的关系决定了畸变。该类畸变的特点是畸变沿着透镜半径方向分布，称为径向畸变，径向畸变主要包括桶形畸变 barrel和枕形畸变 pincushion两种。针孔模型中，一条直线投影到像平面仍是直线。而摄像机的透镜往往使得真实环境中的直线投影为曲线“curvilinear” 。越靠近图像边缘，这种线性越明显。邮寄实际加工制作的透镜往往是中心对称的，这使得不规则的畸变通常径向对称。径向畸变随着焦距的减小而增加。
相机的组装工艺中透镜和成像面不严格平行：这一工艺问题造成的畸变，畸变沿切线方向发生变化，称为 切向畸变。其实，切向畸变又分为薄透镜畸变和离心畸变等，具体内容就不细讲了。
李恒大神告诉我说：搞懂径向畸变这块需要几何光学的基础知识，我表示没有学过，也不懂，不过看官们似乎大致知道怎么回事就行了。
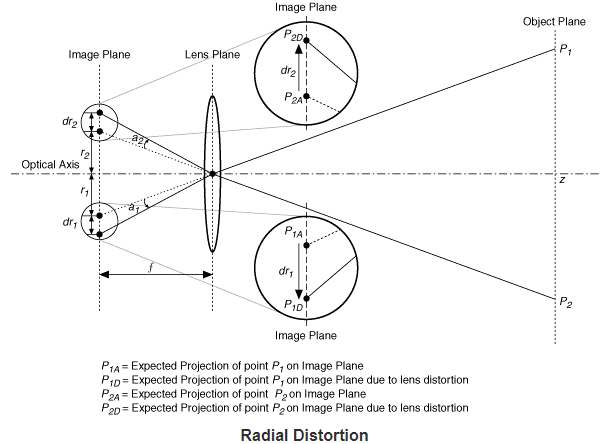
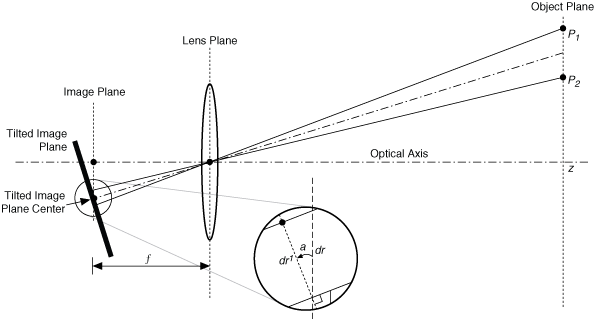
我们假设成像平面上的任意一点 ，写成极坐标的形式为 ，其中 表示点 与坐标系原点之间的距离， 表示与水平轴的夹角。因此：
径向畸变可以看成坐标点沿着长度方向发生了变化，也就是距离原点的长度 发生变化；切向畸变可以看成坐标点沿着切线方向发生变化，也就是水平角 发生变化。
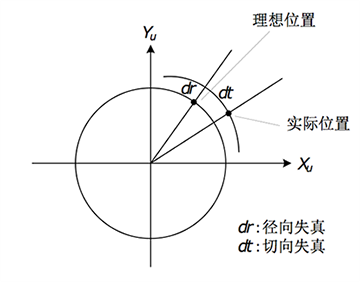
（诸位看官，请仔细理解这几幅图的含义）
3. 畸变校正模型
畸变的数学模型与畸变校正公式
李二看大家毫无反应，也不生气也不着急，慢悠悠说道：我默认大家都理解了啊（这话怎么听着这么熟悉呢，嘿嘿）。
开始敲重点了其实我们的目的不是为了了解畸变而了解畸变，而是为了了解之后对畸变进行校正，消除畸变的影响。我们上面讲解了畸变的类型与产生原理，那么如何对这些
畸变进行建模呢？
研究人员们构建了很多模型，这里呢我们不对模型的推导进行讲解(李二说这话时心里有点发虚，因为他自己也不知道这些模型是如何推导而来的)。不妨直接看看一下畸变的数学模型是什么样子的。
假设无畸变时点 在图像物理坐标系中的坐标为，畸变后该点的坐标为 ，则二者的畸变数学模型为：
->径向畸变数学模型<-
呈现多项式关系，一般采用三个参数 ，当然视情况而定，如果畸变很小，可以少用一个高阶参数。
->切向畸变数学模型<- 具有两个参数。
联合公式(1)和(2)，我们可以通过5个畸变参数校正畸变，也就是找到这个点在像平面的正确位置。
->畸变校正公式<-
李二如同很多老师那般，开启了典型的问话模式：大家还记得上节课中所讲的
总体变换矩阵吗？
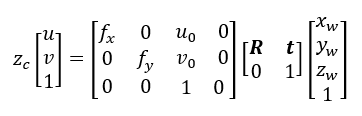
我在下面小声嘟囔：老师们怎么向来都爱这么问，学生肯定不记得呀，有几个学生会复习呀。我们学生的记忆时间似乎比鱼长那么一点点。
李二似乎听到了似的，便道：不记得没关系，我挑个重点说一下。我们由
相机坐标系转换为图像物理坐标系的公式是：
由
图像物理坐标系转换为图像像素坐标系的公式是：
(各位看官可以与上一期对照着看，上一讲采用矩阵的形式，这里采用代数的形式)
李二突然又敲起重点了：上面的公式(4-5)无疑是正确的，只是稍微有点扭捏。如果咱们的相机内参数()或者() 都放在一个矩阵或者一组公式中多好呀，否则每次变换用到内参数时，都要用以上两组公式，现在我们不妨把内参数都写到一组公式中。则有以下形式：
由相机坐标系转换为 归一化的图像物理坐标系的公式是：
(大家看，这个转换是不是少了一个比例因子 ，也就是说 并不是图像物理坐标系 中的坐标了，而是一个归一化产物，量纲是倍数，而不是 了)
由 归一化的图像物理坐标系转换为图像像素坐标系的公式是：
（估计各位看官看到这可能都不想看了，可以理解，李二这家伙，废话太多，似乎生怕学生不理解似的。 冷笑一声，哼，你再怎么讲我TM也不理解啊，算了，行有不得，反求诸人吧，还是李二讲的问题。）
李二又在duang duang duang (咋就是打不出Duang这个字！)，理论部分的最重的重点来了：大家且忍耐数分钟之不关闭本网页，我下面有一推导，欲使图像畸而复正，讲解幽而复明(改自姜伯约)。
我们已知的是畸变后的图像ImgD(ud,vd)(就是你们的相机拍照后得到的图像)，要得到正常的(没有畸变的)图像ImgR(u,v)，就要通过畸变模型建立二者之间的映射关系。
假设正常图像的坐标 ，如果能知道其在畸变图像中的坐标 ，就能够从畸变图像中 位置处取得像素值DN值，并放在正常图像的 处，这样把每个正常图像的像元坐标都遍历一遍(注意：此时只是一个空矩阵哦)，就能够输出正常图像了(注意：这时的正常图像才是肉眼可见的图像，比如图像中显示的是“李二的阳台”)。
开始推导喽，非常简单，李二为了让大家看的更明白，不厌其烦地多写了些字（其实只要联立公式(7) (3) (7)即可，但是我们还是再明确一下）： 由公式(7)，我们由正常图像中的像素坐标 转换为正常图像的归一化图像物理坐标系中的坐标 ：
由公式(3)，我们将正常图像的归一化图像物理坐标系中的坐标 转换为畸变图像中的归一化图像物理坐标系中的坐标
继续由公式(7)，我们将畸变图像中的归一化图像物理坐标系中的坐标 转换为畸变图像中的像素坐标 ：
举个例子，正常图像的
(5,5)坐标点，经上述推导后，对应的是畸变图像(5.3,5,4)点，那么就将畸变图像中(5.3,5,4)点的像素值假设DN=128，赋值在正常图像的(5,5)坐标点上。由于畸变图像的像素坐标都是整数，因此需要进行一定的插值处理(如：双线性内插)。
李二终于松了一口气，好啦，幽而复明了没有，我的后主们？
却不料这次有个爱思考的家伙站起来：二先生，我基本明白了，不过有个问题是：您讲的是由正常影像的坐标推出畸变图像的坐标。为什么不倒过来做呢？也就是由畸变图像的坐标推导至正常图像的坐标，这样思路不是更直接吗？
李二很高兴：这是个好问题！不这样做的原因是：虽然思路更直接，但是操作有点费劲。因为如果反过来，公式(3)就需要改写，畸变参数就不一样了，而通过 标定方法确定畸变参数时得到的是公式(3)中的参数。如果非得反过来，也不是不行，就是相当费劲而已。
正好下课铃响了，李二说：就讲到这吧，内容太多也不太好。
我高兴异常，暗自道：手抓羊肉的干活去（写着写着哈喇子就留下来了，哪位看官要是过意不去，联系请我吃饭哦，哈哈）
4. 后记
本人有点小伤心，因为把前几篇短文拿给一所谓正经师兄(嘻嘻)去看时，得到了看完第一篇就不想继续看了的’高度评价‘。无妨，要听的进不同意见，不过猜测他本身的农学背景对于这一计算机视觉知识似乎并不感冒。
本人又有些高兴，经过多方探索，终于准备将这些随笔短文或技术文档放在干净的博客园中了(2020.03.31)。然在博客园中，鱼与熊掌不可兼得，为保证markdown格式更为优美，我用了专门的格式工具，但是却把公式转换为图片，且转换的不好；若想保持latex公式优美，直接用博客园的MD编辑器造成其他格式又不好看。难啊！
昨天将第一篇博客发到朋友圈中，意外得到很多看官的赞扬。写这种科普知识不累吗？李二性喜分享，分享优异，不畏劳也。
其实写这些东西还是挺不容易的，因为需要保证自己讲所有的知识点完全理解，保证别给诸位看官们造成错误信息，我导师说过的一句话，一直言犹在耳老师的基本素质之一是：别误人子弟。再次拜谢诸位看官。
