[二维成像与三维重建]系列(3) 成像中的几何变换
关键词：成像模型 成像几何 几何变换 坐标系变换
作者：李二
日期：25/03/020
"计算机视觉、摄影测量的大佬们请轻捶，因为这不是写给你们的，本系列均是写给初学者和非主流从业人员，比如俺们植被遥感。"
上回说到，李二证明了小孔成像模型与薄透镜成像模型是近似等价的，他准备在`三维空间点投影到二维像元`过程中，采用小孔成像模型来探索具体的几何变换形式。
我再次见到李二时，是在**吃饭大学的教十210教室，李二似乎搞到了一个兼职教授的头衔，正在给学生们上课，正好在讲
成像的几何变换这一话题。真是无巧不成书呀。于是我悄悄地做到了最后一排的角落处，安静地看着李二的讲解。
1. 单视图成像几何
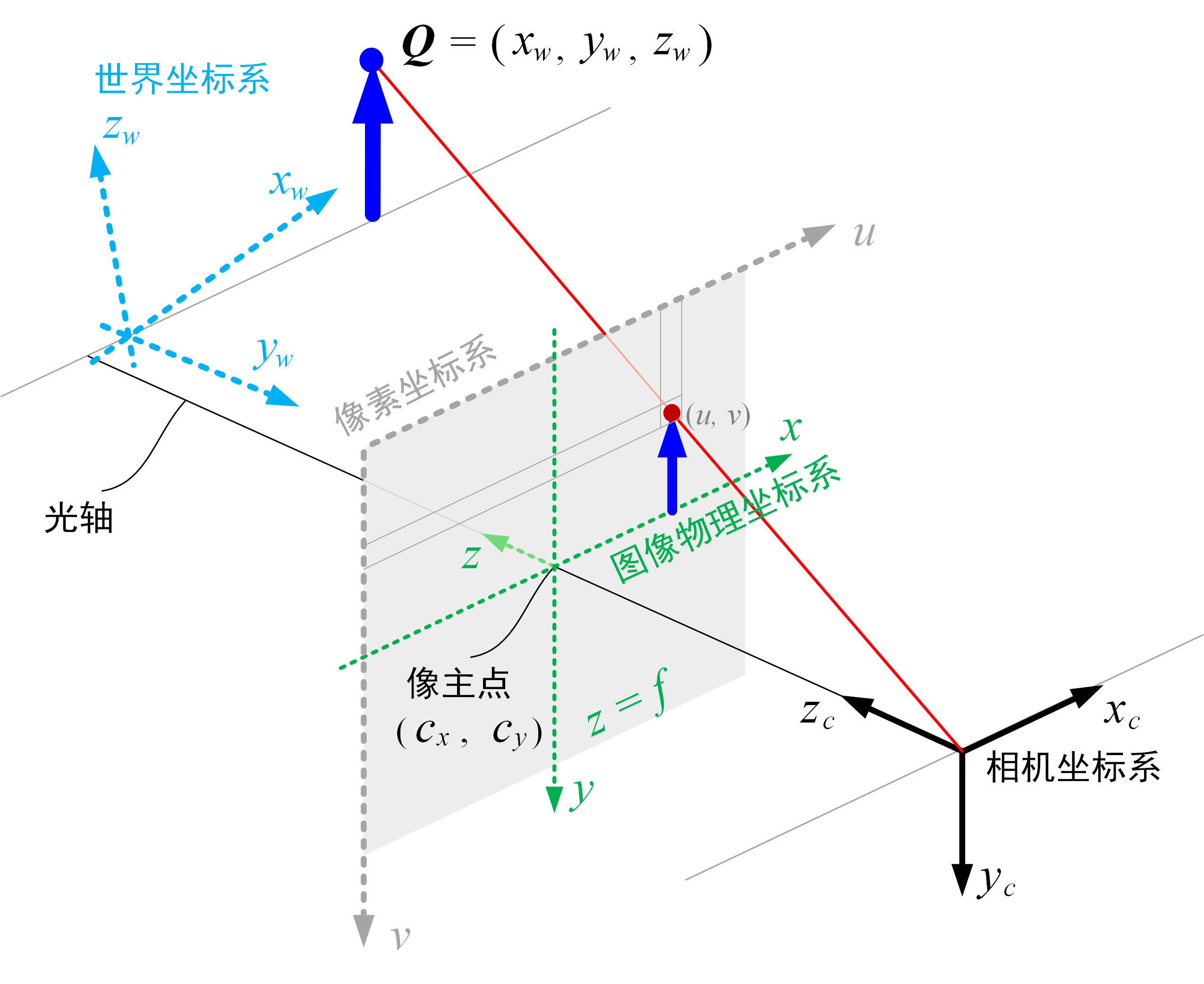
李二的声音很洪亮：一个相机，被放置在一个位置，拍摄得到图像，就是
单视图，在这一单视图成像过程中，三维空间投影到二维空间的几何变换，就叫单视图成像几何。其实，我们看这个图就知道：单一影像的
成像过程可以简化为一系列的几何变换或者坐标系变换，即由代表真实三维空间的世界坐标系经过相机坐标系和图像物理坐标系转换到像素坐标系。大家可能一下听着这么多坐标系名词有点蒙圈，听我娓娓道来吧。
2. 坐标系变换过程
李二缓缓说道：为什么提到坐标系呢？因为我们所处的世界中，人们为了方便不同的测量和表置表示，定义了各种各样的
坐标系。 举个例子：
咱们‘吃饭大学’里的木铎所在的位置，大家一般采用地理坐标系来表示吧，或者学校自己设定的本校局部坐标系，反正无论如何，它是三维的，叫做 世界坐标系；你们手里的相机拍出的学校图像，如果要告诉我木铎所在位置，是不是需要说第多少行第多少列的像素位置，它是二维的，叫做 图像像素坐标系。大概意思明白了吧？
2.1 相机的位置与姿态是核心
第二排有个小个子男生率先问到：二先生，那到底怎么样才能将
世界坐标系中的三维点转换为图像像素坐标系中的二维像素点呢？一般坐标系变换只包含平移、旋转、缩放，我怎么感觉直接转换比较困难呢。
说得好！直接转换是不可能的，最关键的是：如果不知道相机在世界坐标系中所处的位置和成像时的视线方向，根本无法完成转换。
比如说：给你一个三维空间点 ，又告诉你这个点在图像中的对应像素坐标为 ，你知道需要平移多少，旋转多少，缩放多少，才能实现由 到 的转换吗？此时肯定不知道！
所以首先要知道，相机到底是在三维世界中的哪里拍摄的，从哪个角度拍摄的，才能知道大概平移多少，旋转多少。
敲重点：我们需要对相机自身建立一个三维坐标系(
相机坐标系)，这个坐标系作为世界坐标系和图像坐标系的过渡，就能实现三维空间点到二维像素点的变换了。
(上面说了那么多，有的看官可能要着急了，快说具体怎么转换的吧。)
2.2 坐标系的定义
坐标系变换的第0步
我也有点厌烦李二铺垫的太多了，终于李二讲起真格的来了：我们以三维真实空间中的一点 为例，公式化表达该点如何变换到像素点 。在描述具体的坐标变换之前，我们首先定义
四个坐标系：+
世界坐标系(world coordinate system)：以现实三维世界中某一空间点为原点，指定方向为 。该坐标系用于描述相机与物体的位置，单位通常为 。 +相机坐标系(camera coordinate system)：以小孔或相机的焦点(即光心)为原点，光轴射线方向为!$z_c$轴方向并与像平面垂直, 轴分别与像平面的两边平行，单位为 或 。 +图像物理坐标系(film coordinate system)：以像平面的中心或光轴与像面的交点(即像主点)为原点，光轴射线方向为 轴方向并与像平面垂直， 轴的取值总为焦距 ， 轴分别与像平面的两边平行，单位通常为 。(有的人写为二维坐标系，有的人写为三维坐标系，都行！，因为 轴取值总为 ) +像素坐标系(pixel coordinate system)：以图像左上角像素点为原点， 轴分别为图像行方向和列方向平行。该坐标系为二维坐标系，单位为像素 。
(各位看官，下面有点公式，但是不用害怕，我不会细讲公式的推导，只求观其大略，若要察其深，请诸位看官移步计算机视觉或摄影测量书籍)
2.3 世界坐标系转换为相机坐标系 (刚体变换)
坐标系变换的第1步
敲重点：各位注意看，世界坐标系 转换到相机坐标系 时，只存在
平移和旋转，我们亲切地称之为刚体变换 rigid transformation。
既然是三维空间中的旋转，就可能存在三种转轴方向，即绕 轴、绕 轴、绕 轴旋转，相应的旋转角度分别为 。最终会形成一个 旋转矩阵，这个矩阵中的各个元素，可以由以上三个旋转角的函数表示出来。既然是三维空间中的平移，就可能存在三种平移方向，即向 方向、向 方向、向 方向平移，相应的平移量分别为 。最终形成一个 平移向量。
->3个旋转参数和3个平移参数，构成了我们摄影测量中常说的6个外方位元素。<-
(各位看官注意：本文与摄影测量中的转角系统的表示方式并不一致，但是这不影响本文的正确性，摄影测量大佬请轻捶)
在计算机视觉领域，为将缩放变换、旋转变换、平移变换统一写成矩阵乘法的形式，通常采用
齐次坐标 homogeneous coordinates对各种变换进行表示。（大家可以认为齐次坐标就是为了保持各种变换都可以用一连串的矩阵相乘，看着多优美呀）。当然，在摄影测量领域，并不习惯这么表示，无所谓啦，不过看起来整齐多好呀。
（懒得费劲地latex编辑公式了，直接截图的了，不会太多影响观感）
->
<-
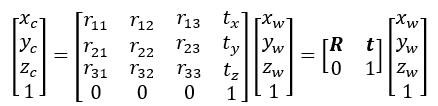->摄影测量中叫外方位元素，计算机视觉中用矩阵表示，叫外参矩阵。<-
2.4 相机坐标系转换为图像物理坐标系 (透视投影变换)
坐标系变换的第2步
再次敲重点：我们继续，相机坐标系 转换到图像物理坐标系 。该变换属于
透视投影变换，即将三维世界中的物体投影到二维平面上，其特点是距离投影中心越远的投影越小，距离越近的投影越大。
透视变换满足相似三角形原理，变换过程仅与相机的焦距 有关。
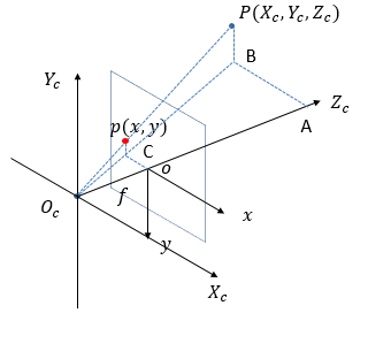
具体的变换公式为：
->
<-
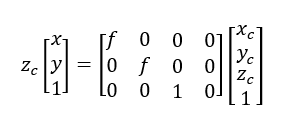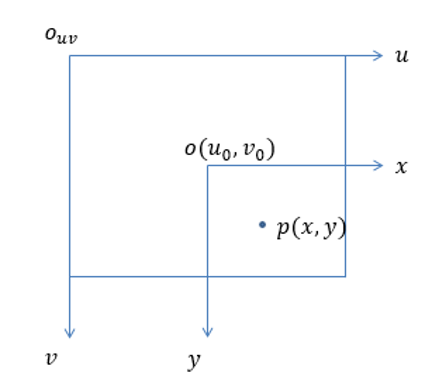
2.5 图像物理坐标系转换为图像像素坐标系
坐标系变换的第3步
三次敲重点：我们再来，图像物理坐标系坐标系 转换到像素坐标系 。这次就比较简单了，因为图像像素坐标系和图像物理坐标系都处于像平面上，只是各自的
坐标原点和度量单位不同：
物理坐标系的单位是物理单位 !$mm$，而像素坐标系的单位是像元 ，二者之间的转换关系为： 或者 。物理坐标系的 坐标原点在像素坐标系中的位置为 处(物理坐标系的坐标原点因为加工原因，可能并不在影像的正中心，存在小小的偏离)。
相机内部自身的三个参数 ，在摄影测量中称为内方位参数。
具体的变换公式为：
->
<-
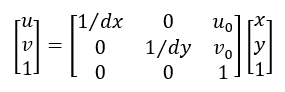->摄影测量中叫内方位元素，计算机视觉中用矩阵表示，叫内参矩阵。<-
2.6 总的坐标系变换的表达
坐标系变换的总结步
最后一次敲重点：李二说，我保证这节课不会再敲了。在我们上面讲的过程中，是完全严格按照
小孔成像模型理论来进行的，因此通过上面四个坐标系的三次转换，我们就可以得到一个点从世界坐标系转换到像素坐标系的总体变换矩阵。 令 , ,
->
<-
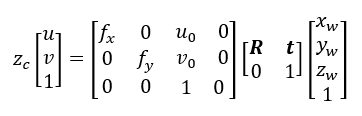总体变换矩阵描述了相机的内方位元素(或内参矩阵)和外方位元素(或外参矩阵)。
李二突然提高了嗓音，便道：值得注意的是：
通过 总体变换矩阵，已知三维空间中的一个三维点，根据相机的内外方位元素，可以确定其在图像中的对应像素点。但是反过来，仅根据相机的内外方位元素，却不能通过图像中的一个像素点确定它在三维空间中的对应点，这是因为总体变换公式左边的 是未知数。
以上就是我们这节课的主要内容，李二如释重负。他环视了一下整个教室，幸好还有约30%的人屁股做的还很稳，只不过剩下的人都在收拾东西，准备吃饭去了。
2.7 为下一讲留个扣子
我对李二了解颇深，知道他要给下节课留个扣子了。哈哈.....
李二有点不高兴了，这还没下课呢，便说道：其实我并没有讲完整，一个重要的问题是：
薄透镜成像模型虽说可以近似为小孔成像模型，但是仍存在一些问题。考虑到
理想化的小孔成像模型确定的坐标变换关系均为线性，并没有考虑现实相机凸透镜成像中由于对光线得不规则折射造成存在的场曲、畸变等问题。因此即根据小孔成像模型计算出来的像点坐标与实际坐标存在偏差。所以，下节课我们要解决这个问题。
3. 后记
本文确保所讲理论是正确的，但是可能与计算机视觉书籍或课程的讲述方式并不一致，尤其是在三维点到二维点的投影变换方面，与计算机视觉课程cs131的讲述方式差别很大，可能是因为李二有一些摄影测量的背景吧，所以更倾向于类似摄影测量的讲解方式，当然，二者是相通的。
