[二维成像与三维重建]系列(2) 相机成像模型
关键词：薄透镜成像模型 小孔成像模型 单视图成像几何
作者：李二
日期：24/03/020
"光学的朋友请轻捶，因为这不是写给你们的，本系列均是写给计算机视觉、遥感等图像处理领域的初学者的。"
上回说到，李二最终用透镜组构建了等价的薄透镜，设计成功了一款相机。最近听说他的兴趣点逐渐转移到图像处理和计算机视觉中了。
这次遇到了李二，我且和他打听打听，到底弄啥嘞。
1. 成像模型的概念
我道：李二，听说你，不当厨师，改成立防忽悠热线了，竟敢扬言再也不上当受骗了？直逼我心里防线了。
李二自从设计成功相机，便像变了一个人，正襟危言道：你这梗，我不懂！不过我知道你的意思是想问我最近在做什么。
本人呢，尝试通过相机，拍摄点图像，来恢复真实世界的三维结构。目前处于第一步，研究
相机的成像几何，因为成像的过程其实可以简化为一系列的几何变换。我通过模型化这个成像过程，就得到成像模型。
->成像模型的概念<-
相机通过拍摄图像，可以将三维世界中的物体投影到二维图像中。成像模型其实就是建立三维空间到二维空间的投影映射关系。
2. 小孔成像模型
那我今天不妨做一次'客'，你当一次'东方生'，咱们来次
答客难（最喜欢的文章之一）。首先，既然你要将成像过程模型化，那么你是如何模型化的呢？
李二先生喟然长息，仰而应之曰：我采用最简单的小孔成像模型，即相机可以抽象为一个
小孔加一个成像平面，成像平面与小孔之间的距离为焦距。注意，小孔位于成像平面和待成像的三维场景之间，任何来自真实世界的光只有通过小孔才能到达成像平面。通常为了简化模型运算，在小孔与三维场景之间建立一个
等效成像平面，该等效平面与小孔的距离仍为焦距，且具有与原成像平面等价的成像几何关系，区别仅在于成像为正像。
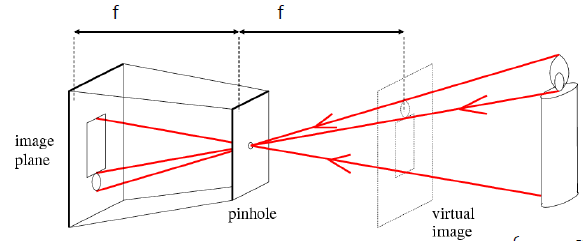
（ 顺便秀一下我自己画的一个图，既然我是做植被遥感的，那贴张树的吧）
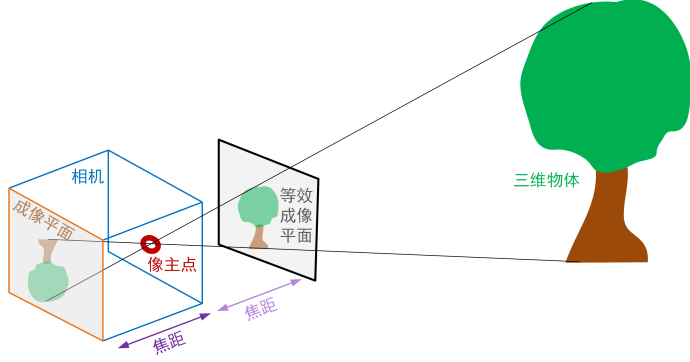
李二继续说：接下来我们看一下怎么把三维空间中的点，投影到二维平面上。按图说话：
假设三维空间中，以小孔中心为
原点，以主光轴(即穿过小孔并与成像平面垂直的直线)的朝向像平面方向为轴方向，坐标轴轴和轴分别像平面两边平行：有一个点，光线由点经相机的
小孔到达二维成像平面上的点，根据相似三角形原理，我们可知：
注意：
这里始终为负数，为正数； 小孔成像成的是倒像。
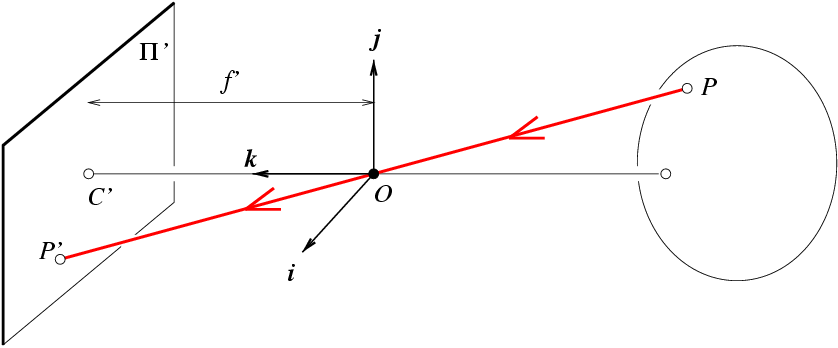
稍等稍等，第一个问题，我看你最终设计的现代化相机最终呈现的都是
正像而不是倒像，而且你刚刚说到等效像平面了，为啥不弄一个正像的公式。
那非常简单，如下：
注意：这是等效像平面的公式，其几何关系与真实像平面的几何关系等价。
3. 薄透镜成像模型
第二个问题，就比较严肃和重要了！我记得上回你说过，你设计的
透镜组可以等价为薄透镜，那么薄透镜成像模型是否依然可以使用小孔成像模型来代替？
李二好不慌张的说道：答案是肯定的，薄透镜成像模型可以采用小孔成像模型来替代。不信看下图。
根据图中的相似三角形，依然可得：
注意，此时
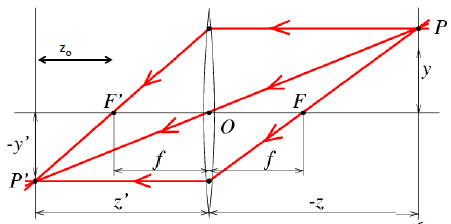
敲重点：回顾上回说的薄透镜
物距-像距-焦距之间关系公式：当物距无穷远时，也就有 像距 = 焦距。事实上，一般10倍以上焦距就是足够远了，通常拍摄情况均可以认为物距无穷远。
也就是说，在物距无穷远情况下，公式中的可以忽略不计，可认为。哈哈，这个时候薄透镜相机的投影公式和小孔相机的投影公式就一模一样了。
李二，不错呀，其实我早就知道
茴的四种写法了。只不过，我喜欢看你认真表演的样子。期待你进一步的研究工作。
4. 后记
成像模型是计算机视觉最基础的内容，建议各位看官一定要搞懂。
下一篇文章将介绍成像模型中具体的几何变换，是我认为计算机视觉和摄影测量中十分十分重要的内容，公式稍微有点多，但是并不复杂。
最后，李二试图让即使初学者都能容易的理解，而且具有代入感，所以废话比较多。部分看官就不要太较真了。
