[二维成像与三维重建]系列(1) 如何设计一个相机
关键词：无镜头成像 小孔成像 透镜成像
作者：李二
日期：24/03/020
"光学的朋友请轻捶，因为这不是写给你们的，本系列均是写给计算机视觉、遥感等图像处理领域的初学者的。"
想象一下，上帝突然把世界上的所有相机和设计图纸甚至相机技术人员的记忆都删除了，而世界人民指望李二重新完成相机的开发，李二怎么办呢？
我正好记录下了李二的思考过程，请各位看官细细看来！
1. 无镜头成像
李二的第一次尝试
李二搞到了一块成像传感器CCD阵列，然后说：直接把CCD阵列放到要拍摄景物的前面就好了。李二名之曰
无镜头成像，并志得意满的翘起了二郎腿。
幸好我读过几天相关专业的书，于是说道：感觉不太行呀，目标物上任意一个点都会向四面八方都反射太阳光，估计你传感器上的每个像元都能接收到这个点的反射信号，换言之，目标点与像元点不是一一对应的。不信你看下图。
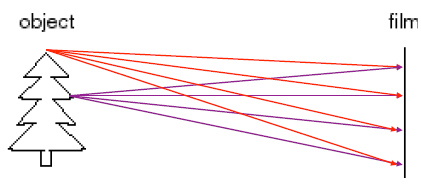
我继续说道：不仅如此，由上图看，一个像元点还会接到很多目标点的反射信号，这个像元实际接收的信号乱七八糟的，像元模糊的厉害。成的像根本不知道是个啥！
李二若有所思.... 然而，他突然梗起脖子说道，那为啥平面镜就可以？我每次照镜子都能看自己很清楚呀，为什么放平面镜在目标前方能行，放CCD在物体前方就不行呢？
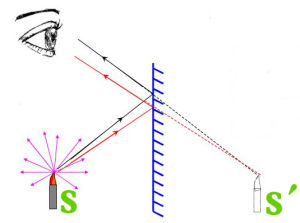
我正色道：此大谬矣！平面镜与CCD的最关键的差别是
有无镜面反射能力。平面镜正因为其镜面反射特性，导致物点与人们看到的像点是一一对应的。每个物点向四面八方发射的光线，经镜面反射到人眼，又重新聚集到像平面。还是看图说话。
李二恍然大悟，原来如此。那我再想想有什么其他办法。
2. 小孔成像
李二的第二次尝试
过了几天，我再次见到了李二，他说经过了几天的琢磨，我想到了一个成像的好办法。我一想，正好最近闲来无事，不妨听听看。
李二说：我要在CCD前面加一个
小孔 pinhole，用栅栏把物点从四面八方射向CCD的光线遮挡住，只让有限方向内的光线透过小孔，这样成像应该就清晰多了。李二把它命名为小孔成像。我给你画个图，你看看。
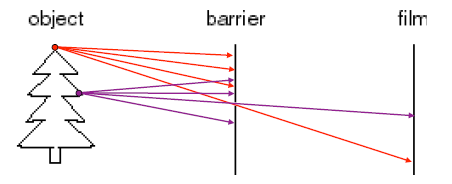
喔，这是一个不错的方式，确实有效！我赞叹道。这基本上能够实现了
目标点与像元点的一一对应。只不过成的是倒像，这倒是没关系。我又道：就是有一个小疑问，这个
小孔的大小(姑且称之为光圈大小 aperture size)，你设置多大合适呢？
李二面露不虞之色，这个随便设置一个得了，能有多大影响？
不然！类似你无镜头成像时的问题。
如果小孔太大，则光线依然会混杂，也就是像元依然接收到多个物点的反射信号(当然这时比无镜头成像已经好很多了)，成像依然比较模糊。 如果小孔太小，虽然是能够物点与像点一一对应了，但是光线的能量太弱了，难以引起CCD上像元器件的光电响应呀，这需要超长时间拍摄(称之为 曝光 exposure)。你要是拍个人物，人家都走了，你还没拍完的。还有一方面，如果小孔超级小，那又涉及到衍射 diffraction问题了，图像又不清楚了。举个例子，黑布上有几个白字，且用不同的小孔大小，拍来试试。估计你会得到下图。
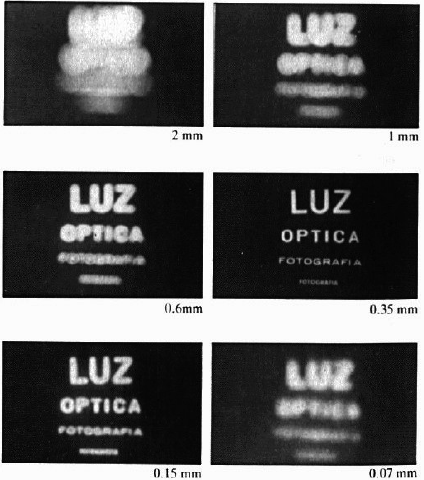
李二这才说道，看来还真是影响比较大。光圈太大，像就模糊；光圈太小，曝光时间就过长。要是找一种方法，可以兼顾二者，就好了。 那我回家再去想想吧。
我说，且慢一步，你再看下面这个图，
3. 透镜成像
李二的第三次尝试 我再次见到李二，已经是一个多月以后了，他有点颜色憔悴，形容枯槁，头发都打绺子了，可是眼里冒着精光。
还没等我问什么，李二拉住我的衣袖(每次写到衣袖，总想起青青子衿)说道：嗨，我似乎找到了一个解决办法，能够兼顾光圈与曝光的问题。我翻书的时候，突然看到了凸透镜，它的光路正好解决这个问题，来看看我手中这个图。
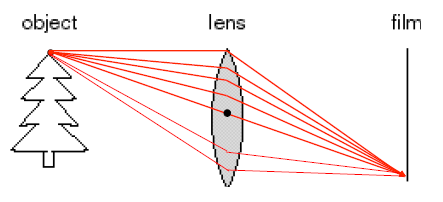
李二继续说道：嘿嘿，这样一个物点向四面八方散射的光线，通过这个凸透镜，就能重新汇聚到一个像点啦。满足你说
物点与像点一一对应和光线的能量足够引起传感器的光电反应啦。影像质量就有保障啦。
果然如此哦。李云龙，你TND还真是个天才。不过我还有个小疑问：
这个凸透镜要放在目标物体与CCD中间的什么位置好呢？
李二当即说道，这个问题已经考虑好了。先给你讲讲凸透镜的性质吧，平行光线经凸透镜会汇聚于一点，称之为
焦点。
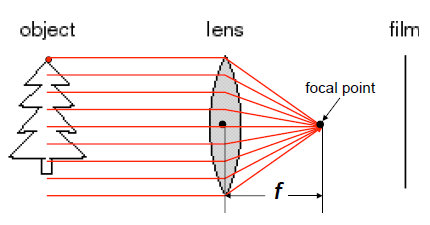
凸透镜有如下4条比较特殊的光线：
平行主轴的入射的光线会折射至另一侧的焦点上; 对薄透镜而言，通过镜心的光线，几可看成是一条没有折射的光线; 通过同侧焦点的光线，经透镜折射后，会在另一侧成为一平行主轴光线; 沿镜心的光线，没有折射的现象;
王多鱼，你TM到底想说点啥？？？
那直接给你上超级无敌海景大床房一套，不对，终极图一个。
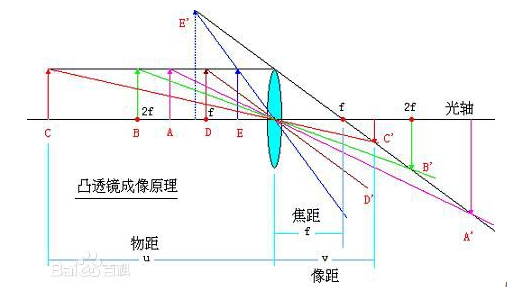
物距：被拍摄物体到凸透镜的距离像距：成像平面到凸透镜的距离焦点：通过凸透镜的平行主光轴的光线，在主光轴上的汇聚点焦距：凸透镜中心到焦点的距离并且我发现了一个公式：。 最终有了一个结论：
当物距在无穷远和两倍焦距之间时，像距在焦距和两倍焦距之间，成倒立缩小的实像，这正好用于相机成像。 当三者之间的位置关系为其他情况时，不适合相机成像，但是有其他用途(各位看官请参考这一博客点击我)。
我不由得说道：李二，士别三日当刮目相待啊。不过其实我想说的是：
谁告诉你透过平行光经过凸透镜会汇聚在一个点上的？其实你说的是一个
十分理想化的情况，是初中课本的知识。我之前看过这样一个图！上图是理想情况，下图是实际情况。
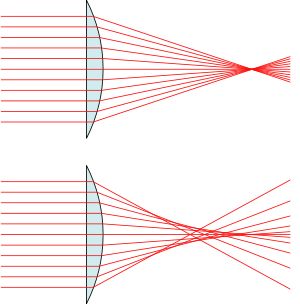
敲重点： 平行光通过一个凸透镜，根本就不是汇聚到一个点，而是越靠近中轴线的光束聚焦得越远，越靠近透镜边缘的光聚焦得越近。这其实是光学误差的一种，叫
球差 spherical aberration。
由上图发现，在实际中，有非常多光线和中轴线交汇的点，其实这些都是焦点，只不过对于特定的某根光线有其特定的焦点,对应特定的焦平面。
可以不用看的知识：在这所有各条光线与其焦点中，一般我们着重考察两个焦点及其对应的光线：
一条是聚焦在最远处的，叫做 近轴焦点 paraxial ray focus；另一条是聚焦在最近处的，叫做 边缘光线焦点 marginal ray focus；
回顾折射定律(
斯涅耳定律 Snell's law)：对上式做
泰勒级数 Taylor series展开，并只取第一项，得到近似相等关系注意，这一近似公式只适用于光线入射角很小的时候，也就是接近中轴线的时候才有效。一般认为，
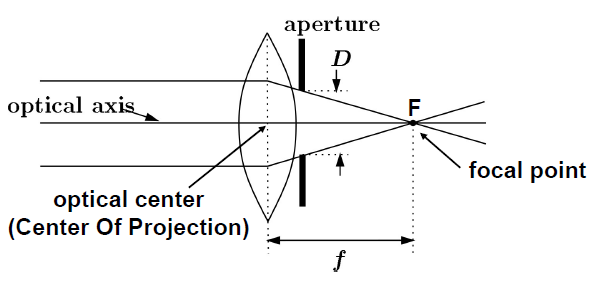
很薄的凸透镜 thin lens近似满足这一公式。而且为了控制近轴光线的范围，人们又在镜头内设置了光圈 aperture，类似下图这样就能保证近轴光线了。当然，光圈可以在镜头的任意一边。
我说到兴头上，便又洋洋洒洒起来：有关
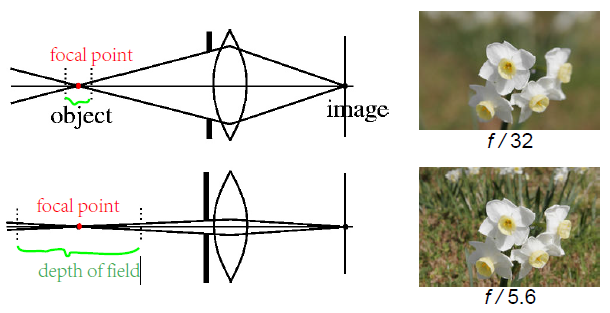
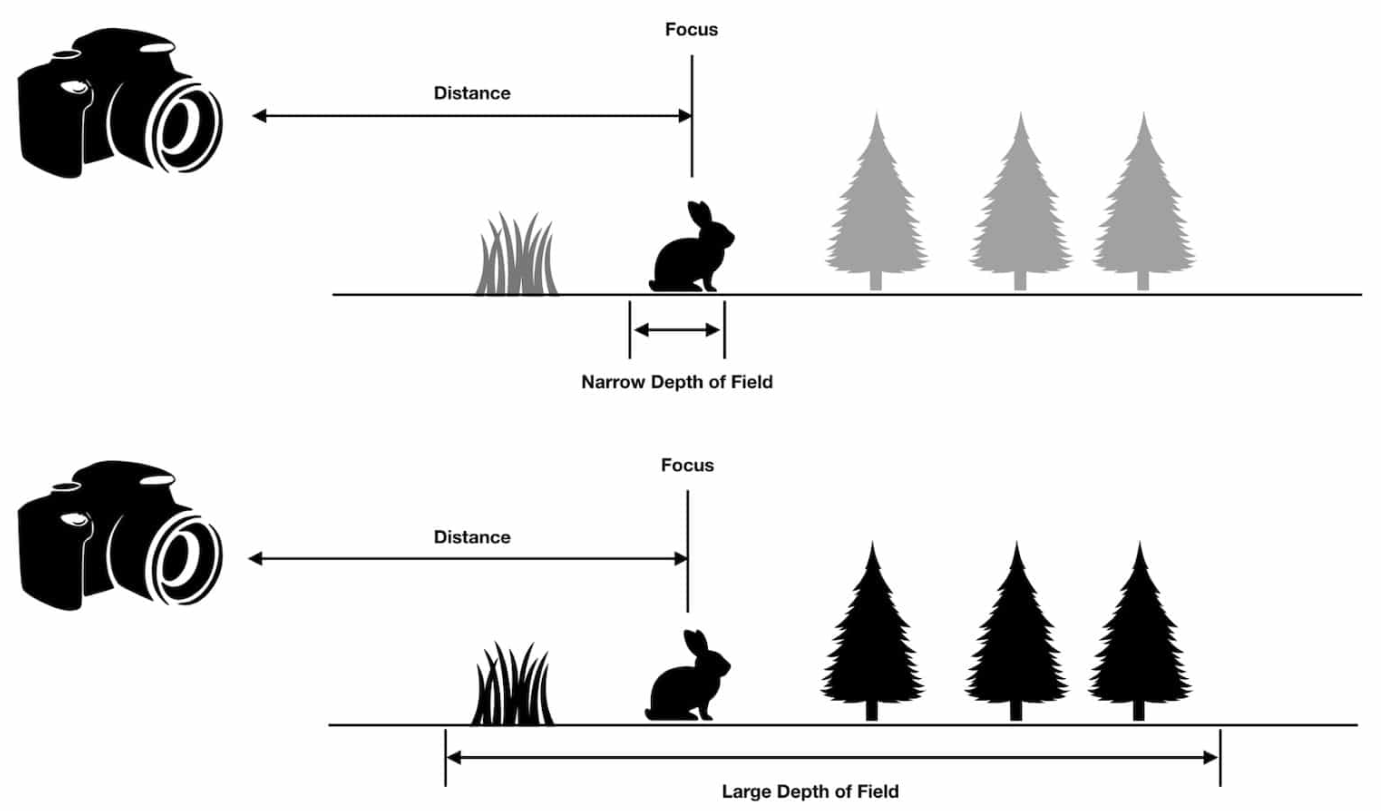
光圈，我还想多说两句。光圈的大小影响近轴光线范围的同时，还会影响景深 depth of field。景深是指相机的焦点前后相对清晰的成像范围。看图说话：小光圈会增大景深，适合清晰拍照，曝光时间要求相对校长 大光圈会减少景深，适合突出人像的人物照，曝光时间要求相对短
听到这，李二终于把志得意满的我打断了，于是问我说，你把你看到的让我看看不得了？(诸位看官若是想看，请点击,并转至李恒大神的回答)
我说李二，你提到的那个物距-像距-焦距公式，是在
近轴光学条件下才能成立的。但是有一点是非常有意思的：当物距无穷远时，，也就有 像距 = 焦距。 而且无穷远并非真的无穷远，一般
10倍以上就是足够远了，认为这个公式成立。 假如有一点真有某种方式使得透镜成像变为理想情况了，这个对于以后成像几何模型建模还是非常有意义的！！！
李二一溜烟跑了，回头向我喊‘我还会回来的.....’
4. 透镜组成像
李二的第四次尝试
已经一年多没有见到李二了，不知他在忙什么，这次我主动过去凑凑热闹，看看有什么进展。
进入李二的房间，一眼就看到他桌子上零零散散的放了一些文件与图片，定睛一看，发现大约是讲
透镜的像差。文章中大概在说：大多数人学到的光学成像理论中，仅用一个透镜，通过调节曲率，获取不同的焦距，然后成像；但在实际应用中，一个透镜会带来很多的像差。其中的一个重要类型就行上面提到的球差。
（各位看官如想看看每种像差的示意图，请点击，也可以参考斯坦福大学的cs131课程）
李二头也不抬的跟我说，我大致研究了一下单一透镜成像的问题，发现一个透镜确实存在各种各样的像差，而且难以全部实现良好校正。不过后来发现，也许多个透镜组成的
透镜组能够消除绝大多数的像差。
(具体的各种像差是如何消除的，fall out of this article，各位看官如有兴趣，请自行查阅几何光学内容)
我问道：有什么进展吗？李二。
李二略显神秘的说：具体内容不方便透露。
但是我已经基本在技术和工艺上实现了通过
透镜组构建消除绝大多数像差的镜头，而且这个透镜组基本满足以上你所说的理想情况了，可以简化认为是一个薄透镜，满足公式
李二继续说：我还发现其实这个薄透镜成像和小孔成像在几何上是可以等价的，今天时间很紧，我就不留你吃饭了，哪天去找你聊。
祝你好运！期待进一步的知识.....
5.后记
我准备给自己挖个坑，根据自己的理解，总结一下二维成像与三维重建。这个系列的文章主要面向‘小白’人员，主要介绍(1)二维图像成像原理；(2)三维点云重建原理。限于自身知识水平，非常高阶的内容咱也讲不了。各位看官权当图个乐，但是李二真诚地希望看完文章，回想一下，各位看官是有些收获的。
声明一下，本人并非`计算机视觉`从业人员，而是一个`植被遥感`的研究僧，所以很多内容理解比较粗浅，望光学大佬和计算机视觉大佬们批评指正。
