数据结构 线性结构(数组[列表] ,链表 单链表的增删改查**, 线性结构的应用 队列 栈[函数的调用**]),非线性结构 树
就是能够用一根线串起来的数据结构
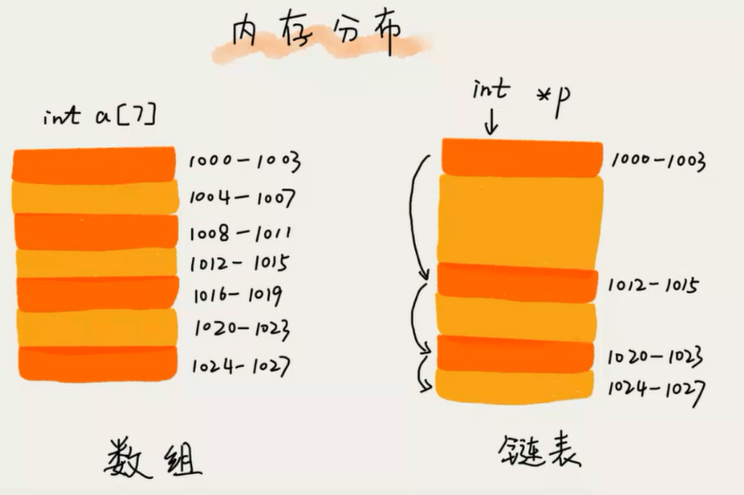

数组 (列表)
问:申请数组的前提条件是啥? a[12]?内存需要满足的条件?
答:a[3] = 首地址(1000) + 索引(3) * 类型长度(4) = 1012 --- 1015 (int类型为4字节)
问:数组首地址从哪获取?
答:数组首地址保存在数组名中
列表中的增(append)删(pop)改(update)查(for)
链表 (约瑟夫,丢手绢问题)
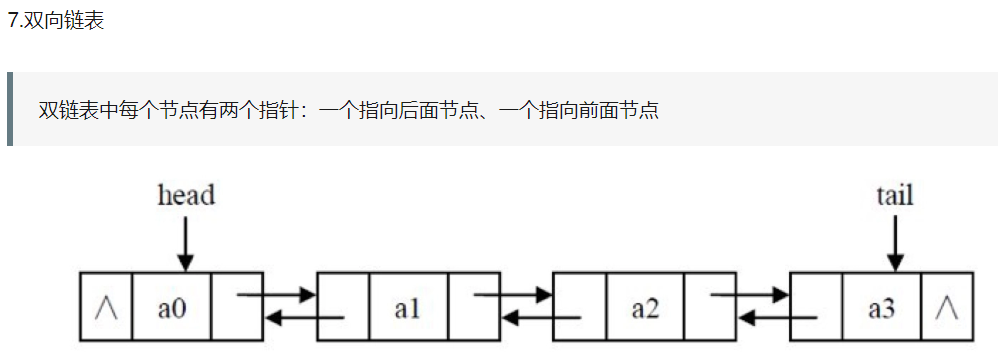
单链表的增删改查
# 梁山好汉排行榜 class Hero(): def __init__(self,no=None,name=None,nickname=None,pNext=None): self.no = no self.name = name self.nickname = nickname #这三个为值域 self.pNext = pNext # 指针域,存内存地址 def add(head,hero): ## head节点不能动,因此需要第三方的临时变量帮助head去遍历 cur = head while cur.pNext != None: ## 把下一个节点的内存地址付给cur, 那此时cur就指向下一个节点 cur = cur.pNext ## 当退出上述循环的时候,cur就已经指向尾节点 cur.pNext = hero def getAll(head): cur = head while cur.pNext != None: cur = cur.pNext print('编号是:%s,名称是:%s,外号是:%s'%(cur.no,cur.name,cur.nickname)) def delHero(head,no): cur = head while cur.pNext != None: if cur.pNext.no == no: break cur = cur.pNext cur.pNext = cur.pNext.pNext head = Hero() # 头结点 h1 = Hero(1,'松江','及时雨') add(head,h1) h2 = Hero(2,'卢俊义', 'xxx') add(head,h2) h3 = Hero(3, '西门庆', 'dsadsad') add(head,h3) getAll(head) delHero(head,2) print('***********') getAll(head)
用链表解决约瑟夫问题(了解)
设编号为1,2,… n的n个人围坐一圈,约定编号为k(1<=k<=n)的人从1开始报数,数到m 的那个人出列,它的下一位又从1开始报数,数到m的那个人又出列,依次类推,直到所有人出列为止,由此产生一个出队编号的序列

# 循环链表 class Child(object): first = None def __init__(self, no = None, pNext = None): self.no = no self.pNext = pNext def addChild(self, n=4): cur = None for i in range(n): child = Child(i + 1) if i == 0: self.first = child self.first.pNext = child cur = self.first else: cur.pNext = child child.pNext = self.first cur = cur.pNext def showChild(self): cur = self.first while cur.pNext != self.first: print("小孩的编号是:%d" % cur.no) cur = cur.pNext print("小孩的编号是: %d" % cur.no) def countChild(self, m, k): tail = self.first while tail.pNext != self.first: tail = tail.pNext # 出来后,已经是在first前面 # 从第几个人开始数 for i in range(k-1): tail = tail.pNext self.first = self.first.pNext # 数两下,就是让first和tail移动一次 # 数三下,就是让first和tail移动两次 while tail != self.first: # 当tail == first 说明只剩一个人 for i in range(m-1): tail = tail.pNext self.first = self.first.pNext self.first = self.first.pNext tail.pNext = self.first print("最后留在圈圈中的人是:%d" % tail.no) c = Child() c.addChild(4) c.showChild() c.countChild(3,2)
线性结构的应用
栈的定义:一种可以实行"先进后出"的存储结构

栈的分类
静态栈:核心是数组,类似于一个连续内存的数组,只能操作其栈顶元素
动态栈:核心是链表

函数的调用**(底层的运行原理):


pop
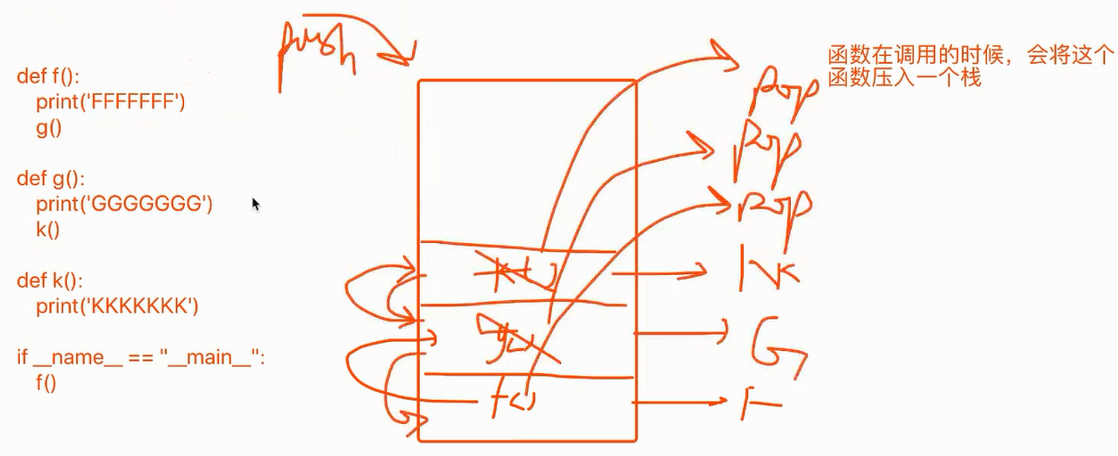
判断:如果栈为空,代表整个函数都已执行完成,释放内存
队列
定义:一种可以实现“先进先出”的数据结构

应用如:生产者消费者模型(操作系统中的概念,各种语言都可以实现)
可以简单的认为:
- 树有且仅有一个根节点
- 有若干个互不相交的子树,这些子树本身也是一颗树
通俗的定义:
1.树就是由节点和边组成的
2.每一个节点只能有一个父节点,但可以有多个子节点。但有一个节点例外,该节点没有父节点,此节点就称为根节点
- 节点
- 父节点
- 子节点
- 子孙
- 堂兄弟
- 兄弟
- 深度
- 从根节点到最底层节点的层数被称为深度,根节点是第一层
- 叶子节点
- 没有子节点的节点
- 度
- 子节点的个数
- 任意一个节点的子节点的个数不受限制 (包括B+树, mysql的索引为B+树)
二叉树
- 定义:任意一个节点的子节点的个数最多是两个,且子节点的位置不可更改
- 满二叉树
- 定义:在不增加层数的前提下,无法再多添加一个节点的二叉树

- 完全二叉树
- 定义:只是删除了满二叉树最底层最右边连续的若干个节点

- 一般二叉树
- 满二叉树
- n个互不相交的数的集合
- 树是数据库中数据组织的一种重要形式
- 操作系统子父进程的关系本身就是一颗树
- 面型对象语言中类的继承关系









