算法与数据结构(十四) 堆排序 (Swift 3.0版)

上篇博客主要讲了冒泡排序、插入排序、希尔排序以及选择排序。本篇博客就来讲一下堆排序（Heap Sort）。看到堆排序这个名字我们就应该知道这种排序方式的特点，就是利用堆来讲我们的序列进行排序。“堆”其实就是一种有着特定结构的完全二叉树，下方将会详细的介绍一下堆。本篇博客讲的就是堆排序，首先我们先对大顶堆，小丁堆进行介绍，然后构建堆，最后利用堆的特性对我们的数据序列进行排序。

下方我们依然是先给出相应内容的示意图，然后给出相应的代码实现，最后就是测试用例了。还是那句话，废话少说，进入今天博客的主题。

 

一、堆

在本篇博客的第一部分，我们先聊一下什么什么是“堆”。在数据结构中的堆其实就是一颗“完全二叉树”，不过此完全二叉树有着一些特殊的规则，根据这些特殊的规则又可以将“堆”分为“大顶堆”和“小顶堆”。大顶堆的特点是该“完全二叉树”的根节点比其左右节点都要大，而小顶堆与其相反，在“小顶堆”中根节点要比左右子节点的值都要小。下方详细的介绍了“大顶堆”和“小顶堆”。

 1、大顶堆

下方这示意图就是大顶堆的规则示意图，其根节点比起左右子节点都大。如果将“堆”的节点按照层次进行编号的话，假设根节点的编号为i(i > 0)的话，那么该根节点的左孩子的编号就为2i, 其右孩子的编号就为2i + 1。那么根据大顶堆的特点，我们很容易就得出k(i) >= k(2i)和k(i) >= k(2i + 1)。根据此特点我们又很容易得出在大顶堆中的根节点是完全二叉树中最大的那个节点。

　　

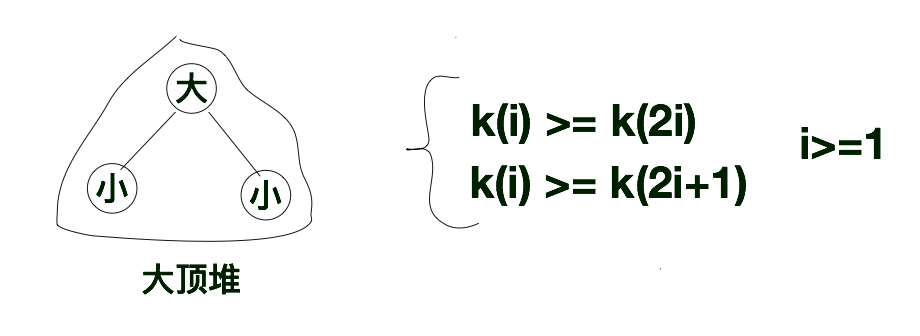
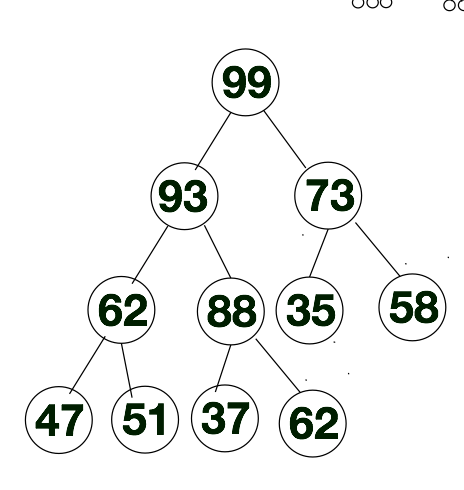
根据上述特点，下方是我们构建的“大顶堆”，如下所示。在大顶堆中，如果我们队大顶堆进行层次遍历的话，层次遍历序列的第一个值肯定是所有序列中最大的那个值。

　　

2、小顶堆

与大顶堆相反，小顶堆则是左右孩子都比根节点大的完全二叉树。与大顶堆规则类似，在小顶堆中k(i)<=k(2i), k(i) <=k(2i+1)（i > 0）。

　　

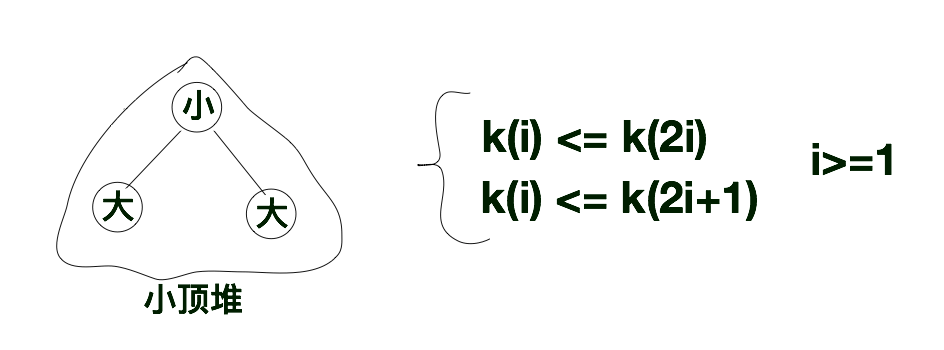
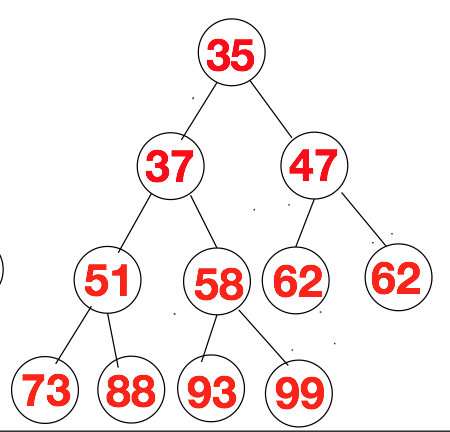
根据上述特点，我们很容易的就给出了小顶堆的结构如下所示。如果我们队小顶堆进行层次遍历的话，层次遍历序列的第一个值肯定是所有序列中最小的那个值。

　　

 

 

二、大顶堆的构建

接下来我们要对[62, 88, 58, 47, 62, 35, 73, 51, 99, 37, 93]进行堆排序，在排序之前，我们需要将该序列构建成大顶堆。更确切的说是根据k(i) >= k(2i)和k(i) >= k(2i + 1)这个规则把该序列转换成大顶堆层次遍历的序列。进一步说，假如大顶堆层次遍历的序列为list, 如果下标是从1开始的话，那么肯定有list[i] > list[2i], list[i]>list[2i + 1](i > 0)这个规则。我们就可以通过这个规则将[62, 88, 58, 47, 62, 35, 73, 51, 99, 37, 93]此序列转换成大顶堆的层次遍历的序列。下方我们会详细的给出方案。

1.大顶堆构建的示意图

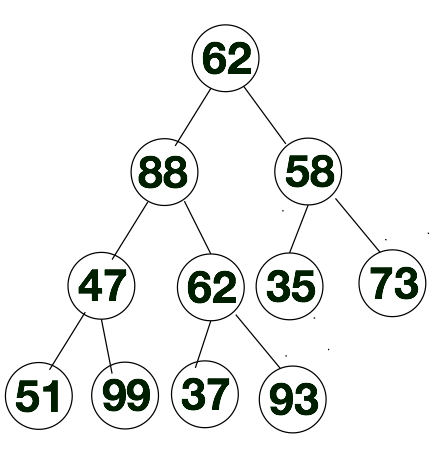
接下来我们将通过示意图的方式来聊一下如何将[62, 88, 58, 47, 62, 35, 73, 51, 99, 37, 93]转换成大顶堆的层次遍历的序列。首先我们先将上述序列从左往右存入完全二叉树中，如下所示。换一种方法来说，上述要排序的序列，也就是下方完全二叉树层次遍历的结果。

　　

2、“大顶堆”的转换 

大顶堆的构建是从下往上进行调整的，确切的说是从局部到整体的来进行大顶堆的创建。在构建大顶堆的过程中，我们先从最小的子树开始调整，然后慢慢的往外扩充。下方是整个过程的示意图，下方会给出详细的介绍。

• (1)、位于“完全二叉树”最下方最小的子树是以62为根节点的子树，我们先对此子树进行调整，将其调整成大顶堆。我们先比较62的两个子节点，比较后我们知道93是子节点中较大的那个。然后62再和93进行比较，我们发现93>62,将62与93交换。该子树的大顶堆构建完毕。

• (2)、以同样的方式我们对以47为根节点的子树和以58为根节点的子树进行调整，将其调整为大顶堆。具体步骤如下方（2）、（3）所示。

• (3)、子树的范围继续扩大，接下来我们要调整根节点为88的子树。88的左右子树都是大顶堆，但是88为根节点的子树不是大顶堆，我们需要从下方的子树中找到88应该在的位置，使其成为大顶堆。88与其较大的子节点99比较，因为99>88将其进行交换。交换完毕后，88的子节点为51和47。88>51，不需要交换，此刻该子树的大顶堆构建完毕。

• (4)、同上一步，我们对整棵树进行调整，最终大顶堆构建完毕。

　　

 

3.代码实现

上述步骤如果理解后，在再给出相应的代码实现并不困难。虽然上面是使用的完全二叉树进行表示的，但是我们在真正进行堆排序的时候并不会用到上述的完全二叉树的结构。仅仅用到了大顶堆层次遍历的序列。所以我们只需要将需要排序的数组根据k(i) >= k(2i)和k(i) >= k(2i + 1)这个规则把该序列转换成大顶堆层次遍历的序列即可。下方就是相应的代码实现。

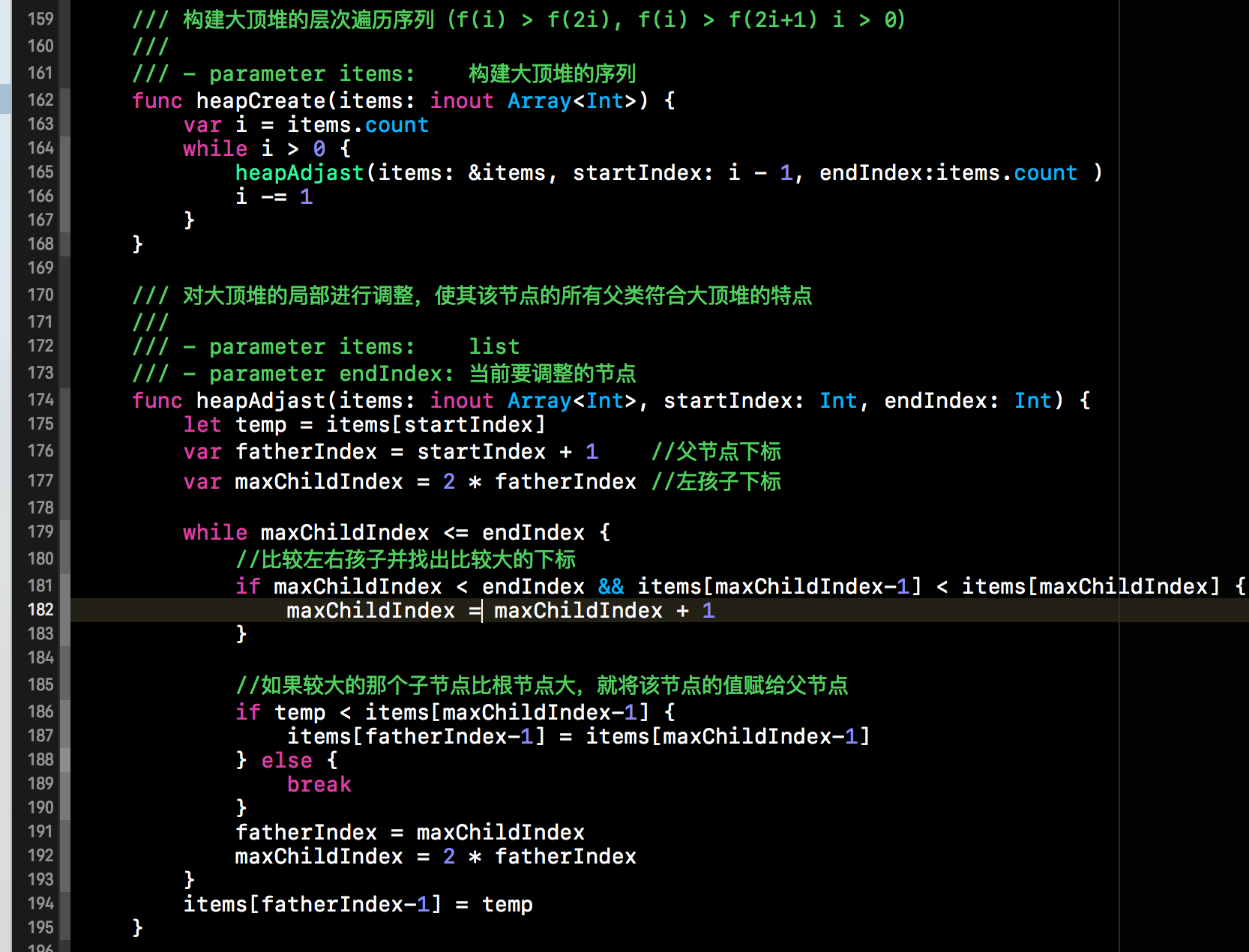
下方截图中的两个函数就是构建大顶堆层次遍历序列的函数。heapCreate()函数就负责将传入的数组转换成大顶堆层次遍历的结构。heapAdjast()方法就负责对子树进行调整。具体代码如下所示：

　　

 

 

三、堆排序的实现

 上面我们将无序的序列转换成了“大顶堆”的层次遍历的结果。接下来我们就要利用大顶堆来进行排序了。本部分将会给出堆排序的详细示意图，然后再根据这些示意图给出相应的代码实现和运行结果。详细内容如下所示：

1、堆排示意图

下方是对“大顶堆”进行的排序，排序后，我们的大顶堆会变成小顶堆，而这个“小顶堆”的层次遍历就是有序的。下方这个示意图就是堆排完整的过程。其实下方的步骤可以总结为下方的两步：

• 将大顶堆的第一个值（整个序列中最大的那个值）与大顶堆最后一个值进行交换。

• 交换后，最后一个值为整个序列中最大值，将此值从大顶堆中剔除。然后将剩余的元素再次进行调整，将其调整为大顶堆。

下方这些示意图其实就是上述两个步骤的不断循环，具体如下所示。

　　

　　

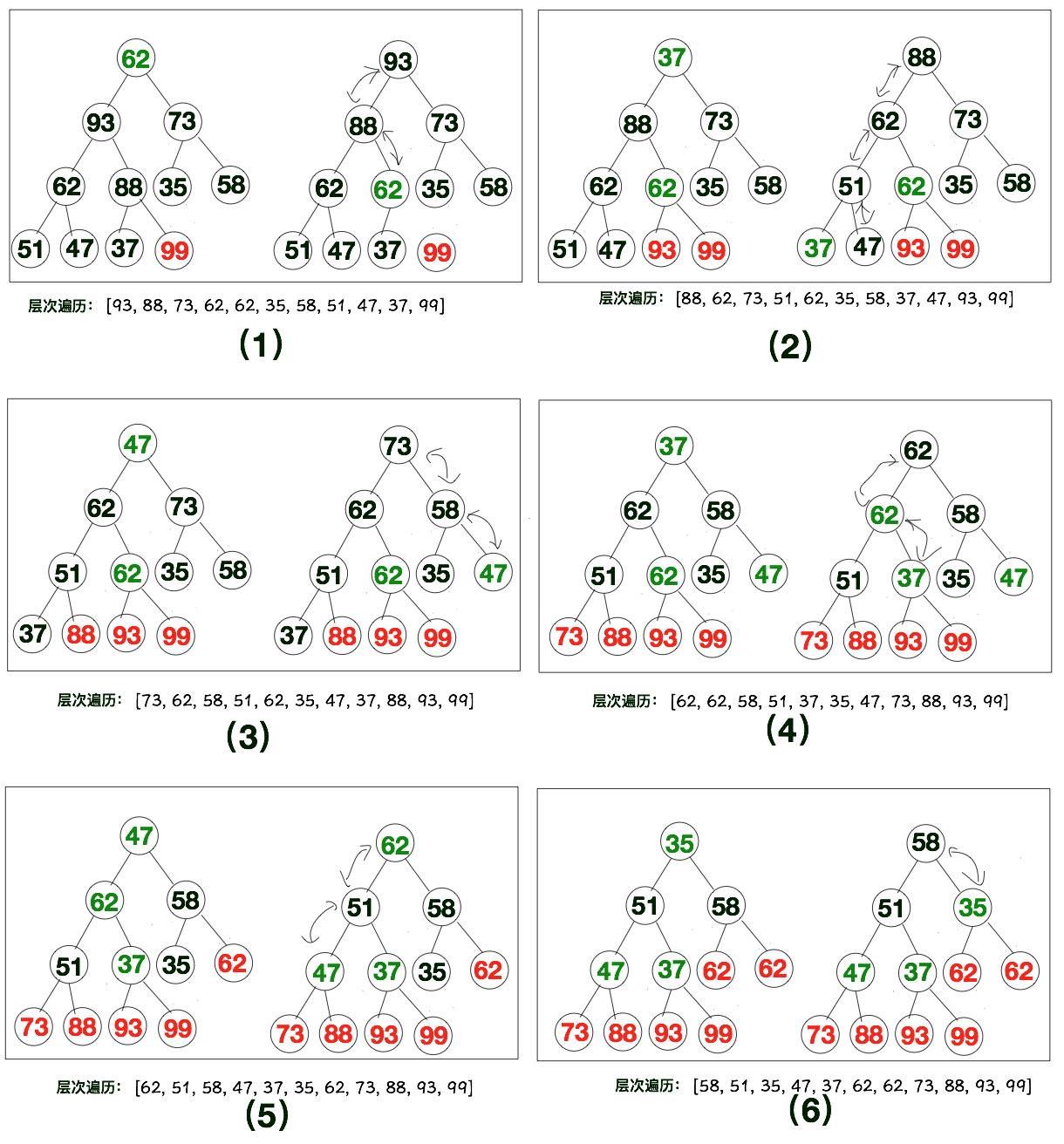
2、调整大顶堆的代码实现

因为将大顶堆第一个值与最后一个值交换后，大顶堆的规则将会被打破，将不再是大顶堆。需要我们从上往下进行调整，上述示意图的方框中的第二部分就是调整的过程。调整后，将会又成为一个新的大顶堆。下方就是调整的具体代码实现，如下所示。

下方代码的核心就是将新的根节点与子节点进行比较，若根节点比子节点中较大的那个节点要小，就要将两者进行交换。重复这个过程，直到成为大顶堆为止。具体做法如下所示。下方这段代码就是上面我们创建大顶堆的那段代码，我们在堆排序的过程中，依然是调用下方的方法来进行大顶堆的调整。

　　

 

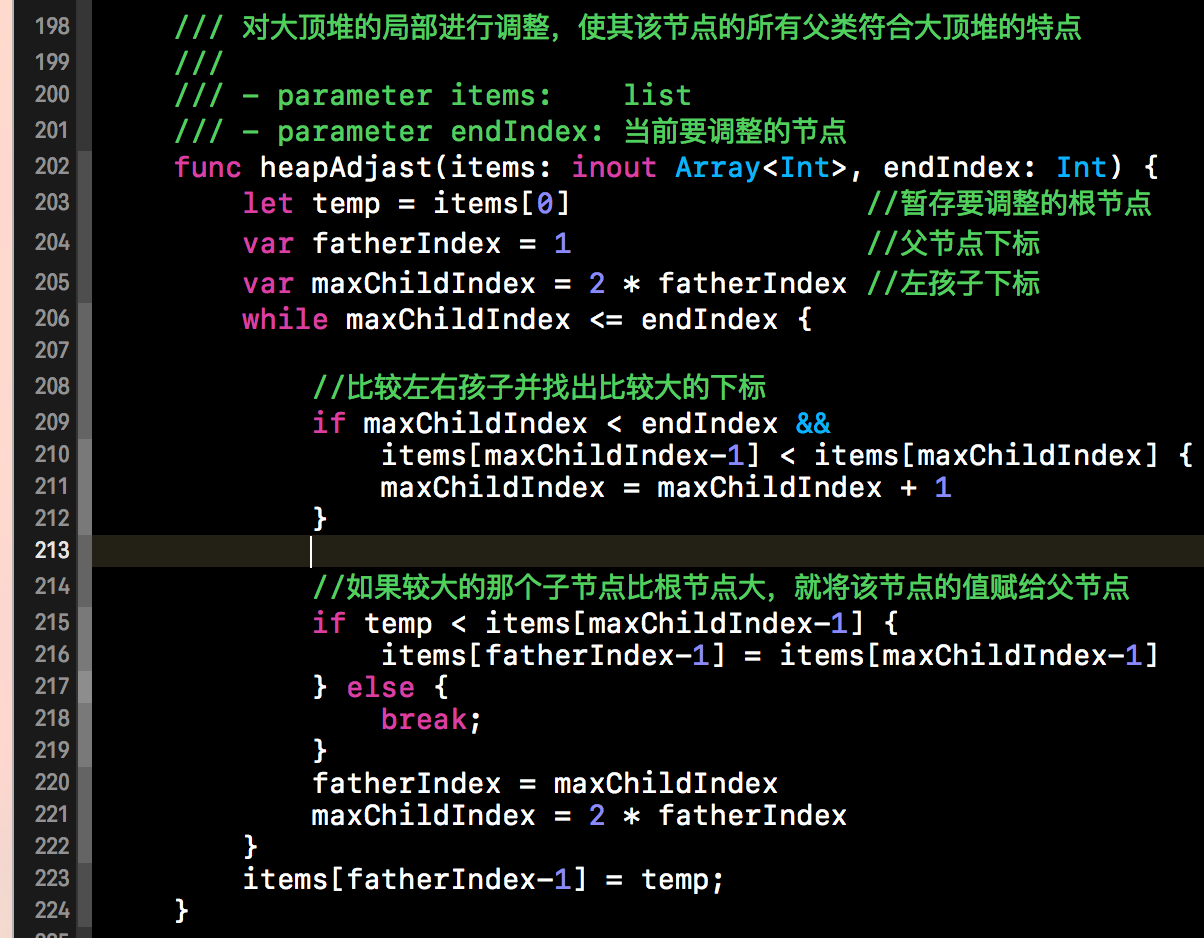
3.堆排序的代码实现

“大顶堆”的创建以及调整上面我们已经给出了相应的代码实现。在上述代码的基础上，给出堆排序的代码并不困难，下方就是堆排序的具体代码实现。

在下方代码中，首先我们将需要排序的序列调用heapCreate()方法将其转换成“大顶堆”的层次遍历的序列。然后将大顶堆的根节点与尾结点进行交换，交换后将大顶堆的长度减一，然后将缩减后的堆调用heapAdjust()进行调整，使其再次成为一个“大顶堆”。使用while不断的循环交换和调整这个过程，知道“大顶堆”中的元素个数为零。具体代码如下所示：

　　

 

4、输出结果

接下来我们就来看看上述代码的运行结果，下方截图中就是相应的运行结果。从下方结果中我们也能清楚的看到，堆排序其实就是不断交换和调整的过程。

　　

 

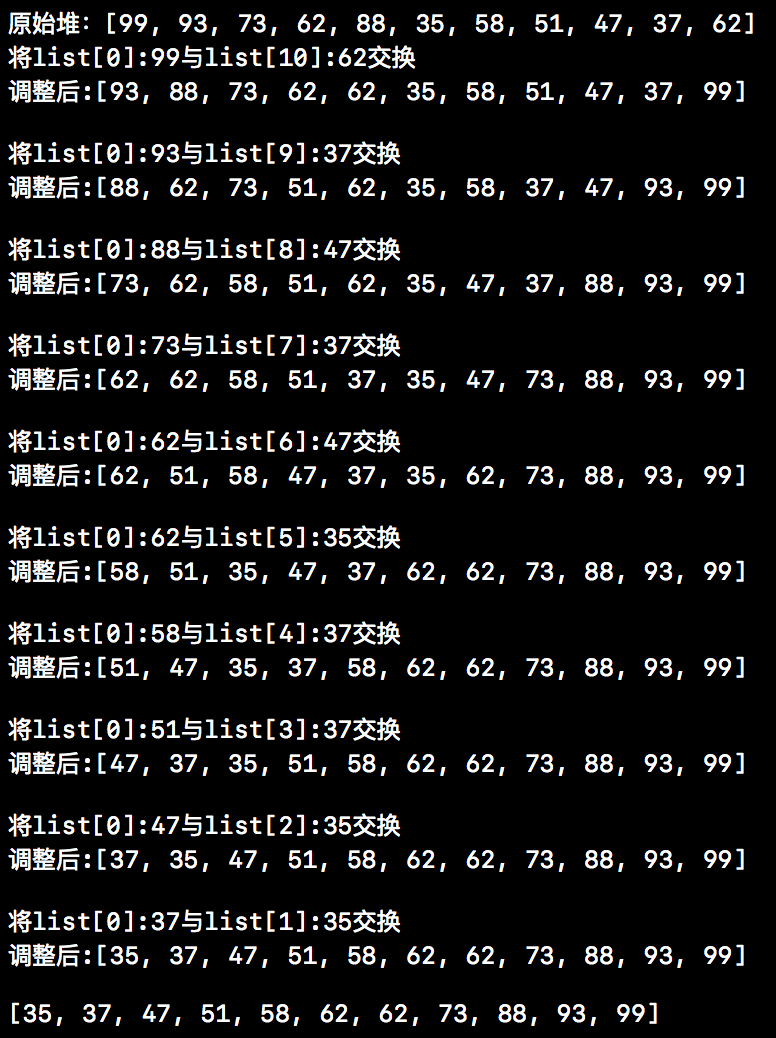
本篇博客对堆排序的介绍就先到这儿，下篇博客我们将会介绍“归并排序”以及“快速排序”的详细内容。本篇博客的相关代码依然会在github上进行分享，下方是github分享地址，如下所示：

github代码分享地址：https://github.com/lizelu/DataStruct-Swift/tree/master/AllKindsOfSort