算法与数据结构(九) 查找表的顺序查找、折半查找、插值查找以及Fibonacci查找(Swift版)

今天这篇博客就聊聊几种常见的查找算法，当然本篇博客只是涉及了部分查找算法，接下来的几篇博客中都将会介绍关于查找的相关内容。本篇博客主要介绍查找表的顺序查找、折半查找、插值查找以及Fibonacci查找。本篇博客会给出相应查找算法的示意图以及相关代码，并且给出相应的测试用例。当然本篇博客依然会使用面向对象语言Swift来实现相应的Demo，并且会在github上进行相关Demo的分享。

查找在生活中是比较常见的，本篇博客所涉及的这几种查找都是基于线性结构的查找。也就是说我们的查找表是一个线性表，我们要查找某个元素在线性表中的位置。顺序查找就是从头到尾一个个进行比较，直到找到为止，此方法适用于无序的查找表。而折半查找、插值查找以及Fibonacci查找的查找表都是有序的，下方的内容会详细的介绍到。进入今天博客的主题。

 

一、查找协议的定义

因为本篇博客我们涉及查找表的多种查找方式，而且查找表的数据结构都是线性结构。基于Swift面向对象语言的特征以及面向接口编程的原则，我们先给我们所有的查找方式定义一个协议。本篇博客中所有的查找方式都会遵循这个查找类型，这样便于外部统一调用，也方便我们测试和扩展。

下方这个SearchType协议就是我们所定义的查找协议。下方这个协议虽然比较简单，但是还是比较重要的，协议中定义了本篇博客所涉及的查找方式对外的调用方式。协议中的search()方法就是外部要调用的方法。该函数第一个参数就是要查找的查找表，第二个参数就是要查找的关键字。该函数的返回值就是关键字在查找表中的位置。如果没有找到就会返回0。

　　

 

二、顺序查找

上面也简单的提了一下，顺序查找表是从头到尾以此进行对比，直到找到我们要查找的元素位置。如果未找到，就返回0。当然从顺序查找的这个过程中我们就可以看出来顺序查找适用于无序的查找表。也就是说，当我们使用顺序查找作用于查找表时，我们是不用关心查找表的顺序的。

为了更直观的理解顺序查找，我们可以看一下下方的示意图。在查找表中存储着A~H的元素，我们要查找G元素在该查找表中的位置，我们需要从A开始以此匹配，当找到G时，就返回G在查找表中的位置。

　　

根据上面我们不难给出代码实现，下方代码这个SequentialSearch这个类就是我们创建的赋值顺序查找的类。当然该类要遵循SearchType，并且给出search()方法的实现。search()方法中的实现内容比较简单，就是一个for循环，依次从头到尾进行匹配。匹配成功后就返回该关键字在线性表中的位置。代码比较简单在此就不做过多赘述了。

　　

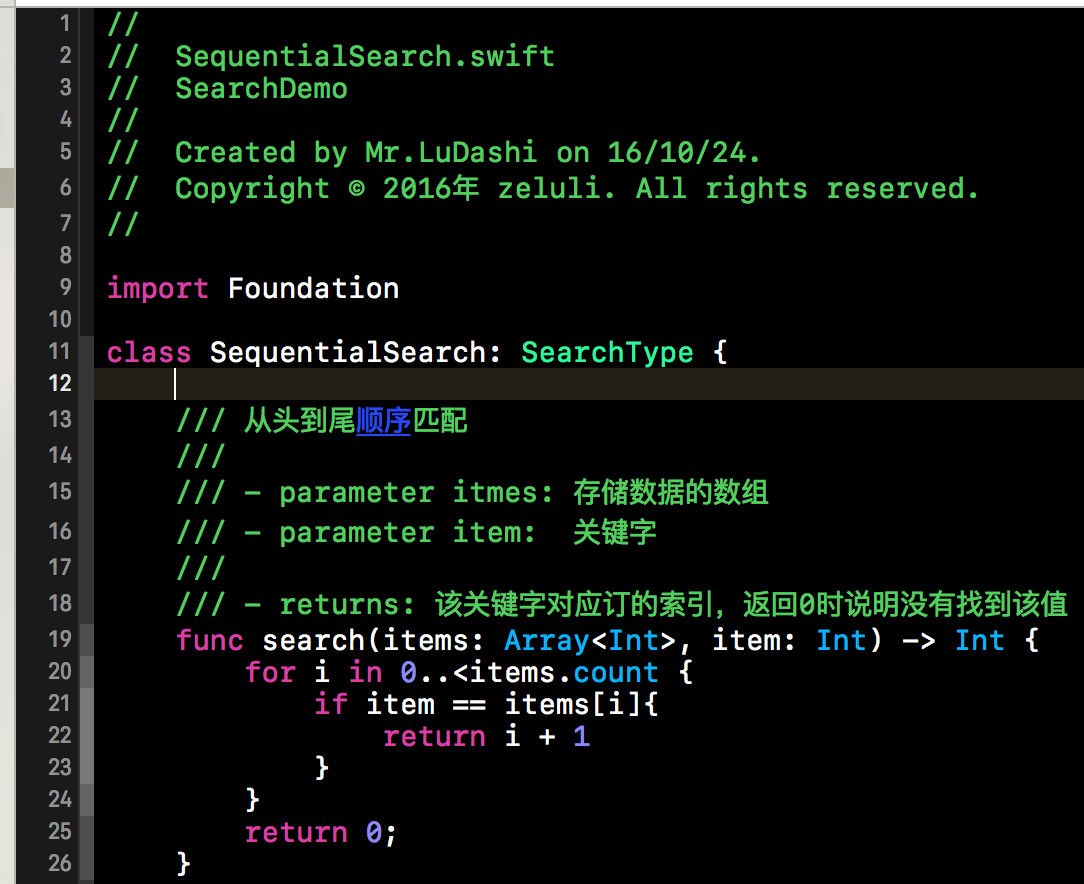
对于顺序查找，我们可以将其进行优化。在的search实现中，i是从范围中取的，所以每次得判断i是否在特定范围中。在我们优化后的代码中就不用做此判断。优化的手段就是将我们要匹配的关键字item追加到查找表的尾部，我们称之为哨兵，如果查找的结果是哨兵的位置，那么说明查找失败，search()函数就返回零。当然你也可以将哨兵放在第一个位置，从后往前的进行查找，不过如果你的查找表是顺序存储的话，不建议将哨兵插入到第一个位置，因为顺序表的插入操作是比较费时的。

　　

根据上面这个示意图，我们不难给出相应的代码实现。下方这个代码片段就是设置了哨兵的顺序查找方法。因为代码比较简单，在此就不做过多赘述了。

　　

 

三、折半查找

折半查找又称为二分查找，折半查找的作用对象是有序的查找表，也就是说，我们的查找表是已经排好序的。之所以称为折半查找，是因为在每次关键字比较时，如果不匹配，则根据匹配结果将查找表一份为二，排除没有关键子的那一半，然后在含有关键字的那一半中继续折半查找。

下方就是折半查找的示意图，在下方示意图中，我们查找A--H这个查找表中关键字G的位置。下方就是每个步骤的具体说明

• （1）标记查找表的范围，查找表的初识范围就是整张表，所以查找表的下边界low=1，查找表的上边界high=8。查找表的中间位置mid=low+(high-low)/2=(high+low)/2 = 4。所以我们将G与mid所对应的D比较大小。比较结果为G>D。

• （2）由上一步的比较结果，我们得知上面一轮中，前一半的数据是没有我们要查找的关键字G的。所以将前一半查找表中的数据进行丢弃，重新定义查找表的范围，因为mid处的元素以及匹配完毕了，要想丢弃前半部分的的数据，我们只需更新查找表的下边界移动到mid后方即可。也就是将查找表的范围缩小到上一步查找表范围的后半部分。此刻查找表的下边界low=mid + 1 = 4+1 = 5。查找表的下边界更新后，mid的位置也会变化，所以我们要对mid进行更新，mid的位置仍然是low和high的中心，mid = (high + low)/2 = (8+5)/2=6。此刻mid处的元素为F, 将G与F比较，可知G > F。

• （3）由G>F这个结果，我们得出，上一轮查找表的前半部分的数据需要丢弃，所以要还需要更新low的值，low= mid + 1 = 6+1 = 7。 mid = (8+7)/2=7。此刻的mid处的元素是G, 所以找到的我们要找的值，返回mid = 7。

　　

 

上面是一个完整的二分查找的实例，不过在上述实例中，只对low和mid的值进行了更新，因为都是抛弃了前半部分。当item<items[mid]时，我们就需要丢弃查找表的后半部分，更新上边距high的值。不难得出，上边边界high的值更新为high=mid-1。将查找表的范围缩小到前半部分继续查找。根据这些叙述，我们不难给出代码实现，下方代码段就是折半查找的Swift语言的实现。如下所示：

　　　　

 

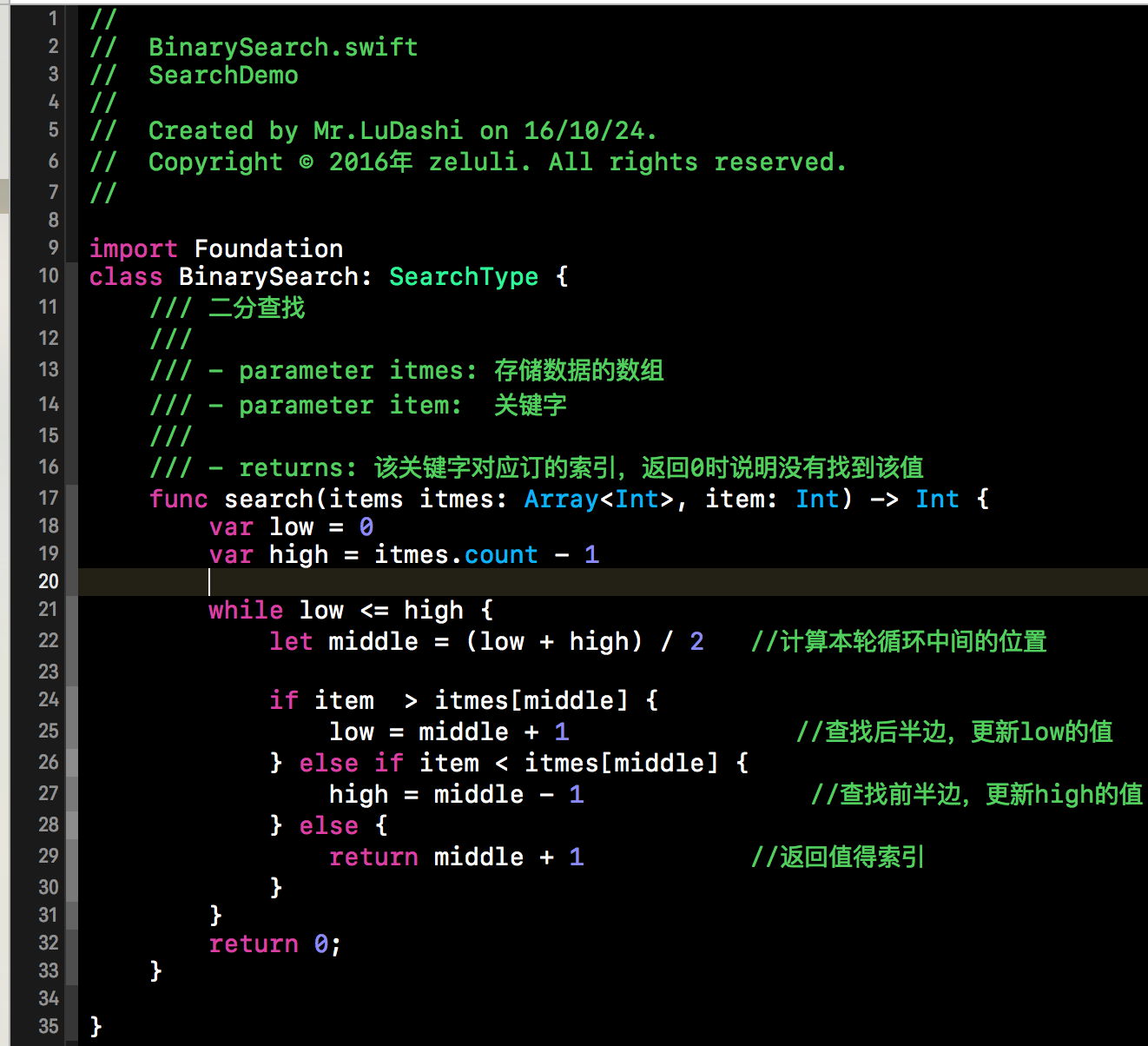
四、插值查找

插值查找其实说白了就是上面二分查找的优化，因为从中间对查找表进行拆分并不是最优的解决方案。因为我们的查找表是有序的，当我们感觉一个值比较大时，会直接从后边来查找。比如举个现实生活中的例子，当你在翻字典是，查找“zhi”相关的字，如果让你直接翻内容的话，你肯定从奔着字典的后边几页去了，而不是从中间进行二分对吧。

插值查找就是让mid更趋近于我们要查找的值，将查找表缩小到更小的范围中，这样查找的效率肯定会提升的。至于如何将mid更趋近于我们要查找的值呢，那么这就是我们“插值查找”要做的事情了。在折半查找中我们知道mid = low + 1/2(high-low)。因为high-low前面的权值是1/2，所以会将查找表进行折半。插值查找就是将这个1/2权值修改成一个更为合理的一个值。

我们将上述的表达式进行修改mid = low + weight*(high-low)，从这个表达式中我们可以看出weight的值越大，mid的值也就也靠后，这符合我们想要的规则。因为我们的查找表是有序的，查找的关键字越大，有越往后，我们就可以根据要查找的关键字来求出weight的值。我们不难求出weight=(key - low)/(high-low)。上面这个表达式就可以求出在当前查找表范围中，我们要查找的这个key值在查找表中的权值。

说这么多，其实插值查找与折半查找的区别就在于mid的计算方法上。下方就是插值查找的一个完整实例。我们要查找82在相应查找表中的位置。具体步骤如下所示:

• (1)、首先初始化我们查找表的范围low=1, high=8。计算我们关键字82在当前查找表范围内的权值weight=(key - low)/(high-low)=(82-10)/(98-10)=0.82。由权值，我们就可以容易的求出mid的值mid = low + weight*(high-low) = 1 + 0.82*(8-1)=6。所以我们将82与items[mid]=79进行比较，可知82>79。

• (2)、由上面82>79的比较结果可知，mid之前的查找表可以被抛弃，所以我们可以查找表的下边界更新为low=mid+1=7。在更新后的查找表中，82对应的权值weight=(82-82)/(98-82)=0。由此刻的weight我们可以求出mid=7+0*(8-7) = 7。此刻我们将82于mid对应的值进行比较，发现匹配成功，将mid进行返回。

　　

上述过程的代码实现并不复杂，只需要将折半查找中的mid的计算方式进行替换即可。下方的InterpolationSearch类就是我们插值查找的类，当然该类也要遵循SearchType协议。在下方代码段中，除了红框部分中的代码，其余的与折半查找的代码完全一致。代码比较简单，在此就不做过多赘述了。

　　

 

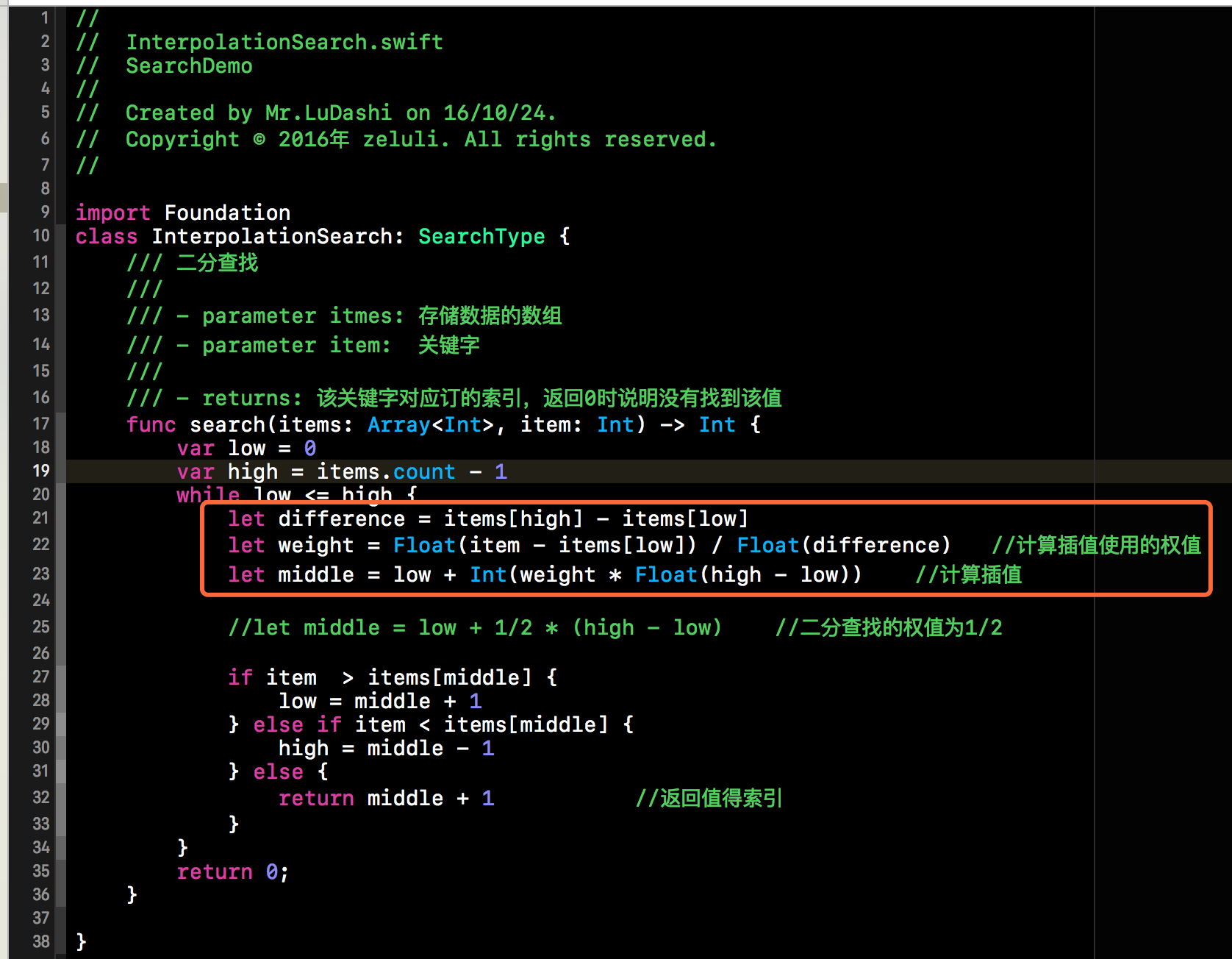
五、Fibonacci查找

接下来我们来聊聊斐波那契（Fibonacci）查找。其实就是按照Fibonacci数列来分隔查找表。如果你之前了解过Fibonacci数列的话，那么Fibonacci查找应该好理解。下方我们生成Fibonacci数列，然后使用该数列对我们的查找表进行分割。

 

1.生成Fibonacci数列

首先我们要生成Fibonacci数列以供我们Fibonacci查找使用。在Fibonacci数列中下一项的值等于前两项的值的和，如果用数学公式来表示的话即为F(n)=F(n-1)+F(n-2)(n>1), F(0)=0, F(1)=1， 根据此规则就可以生成我们的Fibonacci数列。在Fibonacci数列中，n越大，F(n-1)/F(n)的zh值就越接近于0.618，我们知道0.618是黄金分割比，所以斐波那契数列又叫做黄金分割数列。所以我们要实现的Fibonacci查找也可以被称为黄金分割查找。

首先我们先根据Fibonacci数列的规则，来生成Fibonacci数列备用。下方这个就是我们生成Fibonacci数列的方法。下方的FibonacciSearch类就是我们Fibonacci查找的类，其中的fibonacciSequence中存储的就是我们的fibonacci数列。下方的createFibonacciSequence()方法就是创建Fibonacci数列的方法。如下所示：

　　

 

2.Fibonacci查找示意图

Fibonacci查找其实就是利用Fibonacci数列将查找表进行拆分，拆分成F(n-1)和F(n-2)两部分。也就是说如果我们的查找表元素的个数为F(n)，那么low到mid（查找表的前半部分）的元素的个数为F(n-1), 而后半部分（min---high）的元素个数就是F(n-2)。有上述的分割关系，我们可知mid = low + F(n-1) - 1。

说白了，Fibonacci查找其实就是使用Fibonacci数列将查找表进行分割，然后求出mid的位置，将关键字与mid进行比较，然后决定是抛弃后半部分还是前半部分。下方是使用Fibonacci数列查找82在相应查找表的具体步骤。

• （1）、首先准备好Fibonacci数列备用，然后计算查找表元素的个数n在Fibonacci数列中的范围。下方实例中的查找表的个数为9，由F(6)=8 < 9 < F(7)=13这个关系，我们可知查找表从9个元素扩展到13个元素就可以使用斐波那契数列进行分割了，因为F(7)=13, 我们将对7进行标记，也就是key=7。

• （2）、为了可以使用Fibonacci数列进行分割，我们将查找表扩充到13个元素（F(7) = 13）。查找表后边扩充的元素的值与原查找表最后一个元素的保持一致即可。

• （3）、将扩充后的查找表使用Fibonacci数列进行第一轮的分割。因为F(7)=13=F(6) + F(5) = 8 + 5, 所以我们将查找表分为两部分，前半部分的元素个数为F(6)=8个，而后半部分的个数为F(5)=5个，此刻我们的mid的值为mid=low + F(6) -1 = 1+8-1=8。我们将82于mid出的元素进行比较（82<98）。

• （4）、由82<98这个结果我们可以将查找表的范围缩小到上面分割的前半部分。所以我们将high的值进行更新high = mid - 1 = 7。我们继续将前半部分使用Fibonacci数列进行分割，前半部分的个数为F(6)=8, 因为F(6)=F(5)+F(4) = 5+3, 所以我们可以将新的查找表在此分为F(5)=5和F(4)=3两部分。此刻的mid=low+F(5)-1=1+5-1 = 5。82与items[5]=58比较，可以得出82>58，此刻key=6。

• （5）、由82>58这个结果我们可以知道，上一轮的查找表的前半部分应该被丢弃掉。我们将查找表缩小到后半部分（F(4)对应的部分）。后半部分的元素个数为F(4)=3个，我们可以继续将查找表进行拆分，此刻的key=4。我们先更新low的位置，low=mid+1=5+1 = 6。那么mid = low+F(3)-1 = 6+2-1=7。此刻82=items[mid]=items[7]=82, 查找成功将mid返回。

　　

 

3、Fibonacci查找的代码实现

原理分析完毕后，给出代码实现不是什么难事呢。大体结构与二分查找依然类似。就是根据Fibonacci数列来计算mid的值，然后不断的缩小查找表的范围。首先我们需要查找当前查找表需要扩展到几个元素可以被Fibonacci数列进行分割。下方这个函数就是计算查找表扩展后的元素的个数。findNumberInFibonacci()方法有一个参数，这个参数就是当前查找表的元素的个数，该方法的返回值就是扩充后查找表的个数。

　　

 

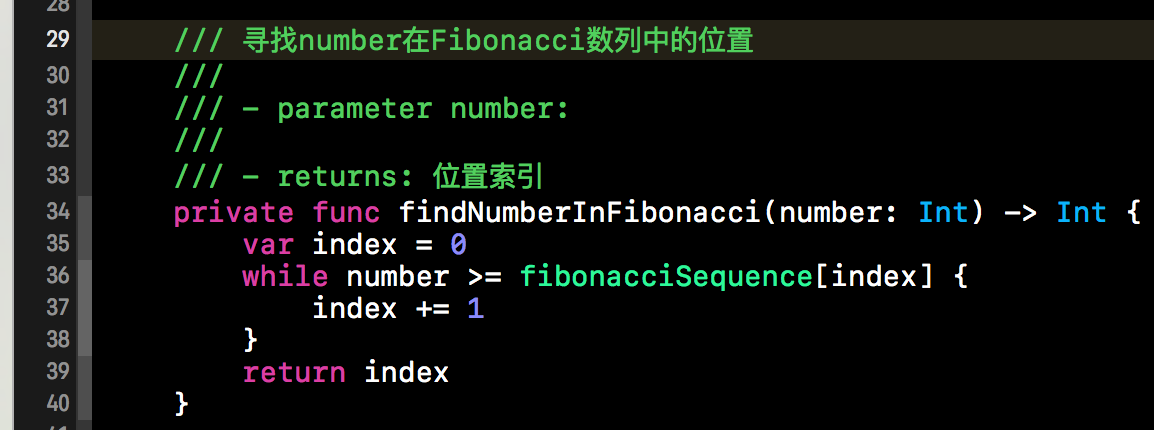
求出要扩充的个数，接下来我们就需呀给查找表进行扩充了。下方这个方法就是对查找表进行扩充。扩充时使用的元素是原查找表最后一个值。

　　

 

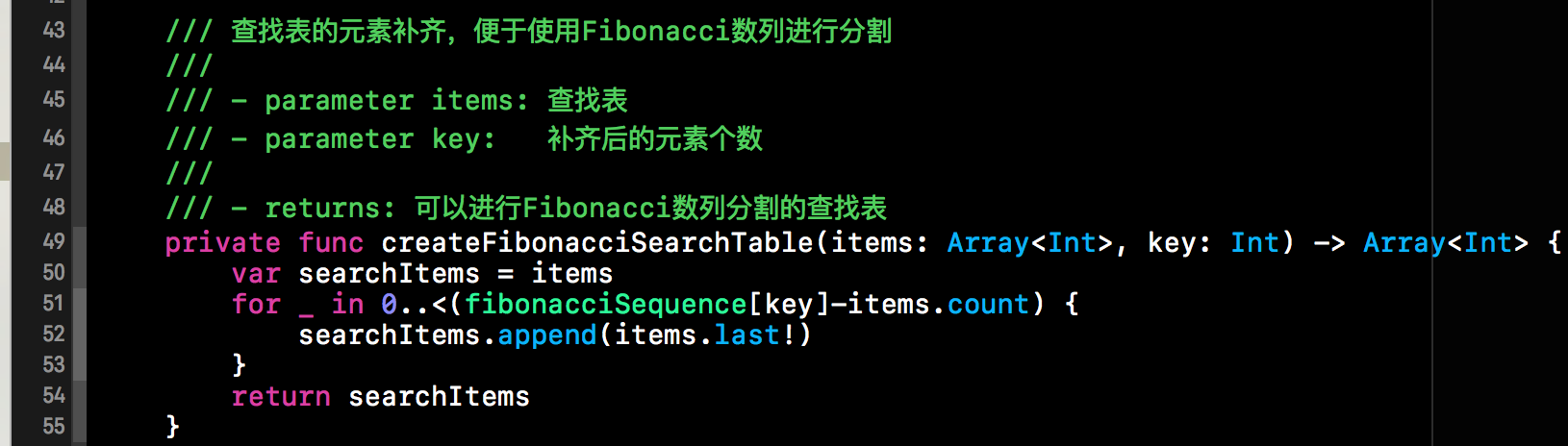
对查找表扩充完毕后，接下来就该进行查找了。下方是Fibonacci查找的核心代码。代码的具体步骤与上述的示例图是一一对应的。需要注意的一点是key值的更新。下方代码中的key其实就是Fibonacci数列的下标，当前范围内查找表的个数==F[key]。因为我们查找表的范围是不断缩小的，所以key值也是会变化的。我们将查找表（查找表的元素个数为F[key]）分割为F[key-1](前半部分)与F[key-2](后半部分)两部分，如果将后半部分进行抛弃，那么key值就为key-1, 如果将前半部分抛弃，那么key=key-2，这一点需要注意。

　　

 

六、测试用例

至此、我们顺序查找、折半查找、插值查找、斐波那契查找聊完了，并且给出了相应的代码实现。接下来就到了我们测试的时间了。因为上面所有的查找类都遵循了一个SearchType协议，所有我们的测试用例可以共用一份，这也是面向接口编程的好处之一。下方就是我们本篇博客的测试用例。

　　

上方的测试用例我们使用的是一个，只要传入不同的查找类的对象，我们就可以使用相应的查找方法进行查找。下方就是我们本篇博客测试用例的输出结果。

　　

本篇博客的篇幅也够长的了，就先到这儿吧，上述实例的完整Demo会在github上进行分享, 下篇博客我们将要介绍其他几种查找方式。

github链接地址：https://github.com/lizelu/DataStruct-Swift/tree/master/SearchDemo