算法与数据结构(六) 迪杰斯特拉算法的最短路径(Swift版)

上篇博客我们详细的介绍了两种经典的最小生成树的算法，本篇博客我们就来详细的讲一下最短路径的经典算法----迪杰斯特拉算法。首先我们先聊一下什么是最短路径，这个还是比较好理解的。比如我要从北京到济南，而从北京到济南有好多条道路，那么最短的那一条就是北京到济南的最短路径，也是我们今天要求的最短路径。

因为最短路径是基于有向图来计算的，所以我们还是使用上几篇关于图的博客中使用的示例。不过我们今天博客中用到的图是有向图，所以我们要讲上篇博客的无向图进行改造，改成有向图，然后在有向图的基础上给出最小生成树的解决方案。本篇博客我们的思路与之前数据结构相关博客的风格保持一致，首先我们先给出迪杰斯特拉算法的原理以及详细的示意图，然后根据这些示意图给出具体的实现方案。

 

一、迪杰斯特拉算法原理解析

在博客的第一部分，我们不谈任何与代码相关的内容，只谈迪杰斯特拉算法的原理以及生成最短路径的具体步骤。下方我们会给出迪杰斯特拉算法的计算最短路径的每一步，并给出每一步具体的说明。废话少说，进入本部分的主题。

 

1、有向带权图

本篇博客依然采取我们之前用的图的结构。不过我们本篇博客使用的是有向图。下方这张图就是是我们之前使用的无向图转换过来的，只是给之前的图的边添加的具体的方向，其他的并为改动。由无向图转换后的有向图如下所示，我们将在下方的图的基础上计算出从A到D的最短路径。

　　

2.迪杰斯特拉算法的具体步骤

下图就是求上图中A->D的最短路径时使用迪杰斯特拉算法的具体步骤。迪杰斯特拉算法主要核心思想是由起始结点开始，慢慢的由尾结点扩散。直到扩展到尾结点位置。下方我们将根据每个步骤给出具体的介绍：

　　

 

• （1）与起始结点A直接相连的点是B和F， 即A->B的距离为10，A->F的距离为11, 所以我们选择A->B这个路径。

• （2）选择B结点后，我们开始探测与B相连的结点，即A->B->G路径长度为26，A->B->I路径长度为22，A->B->C路径长度为28，这三个与上一步留下的A->F（11）相比，A->F（11）的距离最短，所以接下来要探测与F相连的结点。

• （3）F可到达的点是G和E，所以A->F->G的距离为27，A->F->E的距离为37。因为A->F->G(27) 大于A->B->G(26)这个路径，所以由A到G的路径我们依然选择A->B->G(26)这个路径。从A->B->G（26），A->B->I（22）,A->B->C（28）, A->F->E（37）。中选出最短那个距离就是A->B->I（22），所以我们将I作为我们下次探测的结点。

• （4）与I相连的就是D结点，所以我们容易计算出A->B->I->D这条路径的长度为22+21=43。从A->B->I->D（43）, A->B->G（26）, A->B->C（28）, A->F->E（37）这些路径中我们还是选择最小的那一个，不难看出A->B->G（26）这条路径在上述路径集合中最小，所以我们将G结点作为下次路径的探测对象。

• （5）G可到达的结点是H和D, 所以我们可以得到两条新的路径A->B->G->H（26+19=45）和A->B->G->D（26+24=50），因为A->B->G->D(50)这条路径的长度要大于A->B->I->D（43）这条路径的长度，因为这两条路径都是从A到D，所以我们选择较小的A->B->I->D（43）路径。从A->B->G->H（45），A->B->I->D（43）, A->B->C（28）, A->F->E（37）这几条路径中我们依然选择最小的那条路径。从上面这几条数据我们不难看出 A->B->C（28）这条路径最短，所以我们下次要探测的点是C点。

• （6）C点可以到达的点只有D点，所以我们可以得到一条新的路径A->B->C->D, 路径长度为50。因为从A到达D的路径还有A->B->I->D（43），而A->B->C->D(50)这条路径的长度要大一些，A到D点的路径依然选择A->B->I->D（43）。C结点探测完毕，我们从A->B->G->H（45），A->B->I->D（43）， A->F->E（37）几条候选路径中依然选择最小的那一个。不难看出 A->F->E（37）这条路径最小，所以下一步我们要探测E结点。

• （7）E结点可以到达的点为H和D，所以A->F->E(37)这条路径可以延伸为A->F->E->H(44)和A->F->E->G(57)两条边。因为A到H的路径还有一条为A->B->G->H（45），而我们刚生出的这一条要小于之前的那一条，所以A到H的路径更新为A->F->E->H(44)。而A->F->E->G(57)这条A到D的路径要比A->B->I->D（43）要大，所以不进行更新，A到D的路径依然采用A->B->I->D（43）。经过这一步后我们将A->F->E->H(44)和A->B->I->D（43）进行比较，较小的路径为A->B->I->D（43），而D节点又是我们的终点，所以A到D的最短路径为A->B->I->D（43）。

 

3、迪杰斯特拉算法的数据表示

上面是我们使用图形的方式给出了迪杰斯特拉算法的具体步骤，接下来我们会把上面的步骤转换成数据的表示方式，以便于我们使用程序进行计算。下方就是上面这些示意图的的完整的数据表示。下方矩阵中的数据标志着起始节点到该节点的距离。由上到下，以此增加距离的大小，而最上面一排的红色字母，标示着该结点的前驱。下方我们在给出每一个行数据的详细介绍。

• 第一行数据记录了A->B和A->F的信息，当然A->A的距离为0。其他尚不可达的点为-1。

• 第二行在第一行数据的基础上证据了A->B->C, A->B->G, A->B->I的距离信息，因为从第一行数的比较我们可以知道，A->B的距离要小于A->F的距离，所以我们的最短路径要向着A->B->?上发展。

• 第三行的数据则是在第二行的数据上得到的，从第二行数据上我们容易看出，A->F(11)要比A->B->(C, G, I)都要小，所以我们的最短路径要向着A->F->?的放心发展。所以我们找到了A->F->E(37)和A->F->G(28)这条路径。因为A->B->G(26)小于A->F->G(28)，所以A到G的路径不进行更新。

• 第四行的数据则是第三行数据的延伸，我们可以知道A->B->I（2）在当前所有延伸的路径中最小，所以我们要向着A->B->I->? 方向发展。因此我们找到了A->B->I->D(43)这条路径。

• 以此类推……

 

　　

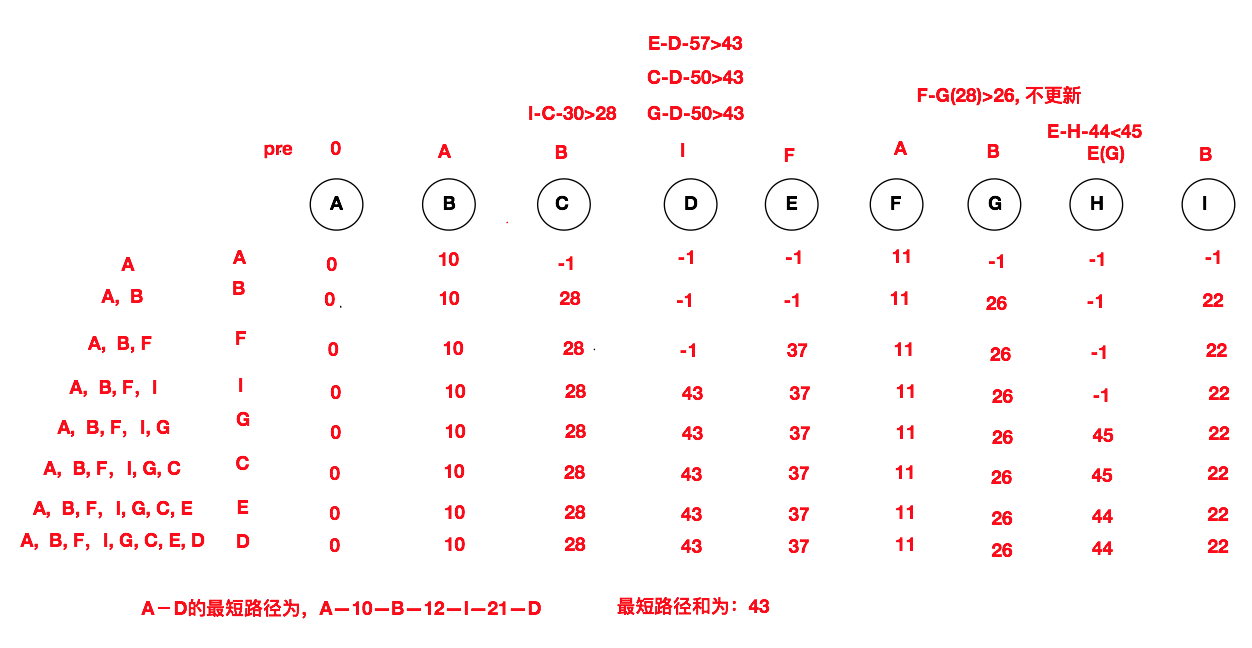
其实上图就是我们之前原理图的数据表示，接下来我们就要根据这些原理图和数据图来给出我们的代码实现，当然我们还是使用Swift语言来实现。

 

二、迪杰斯特拉算法的具体实现

1.上述原理总结

上面说这么多，简单的总结一下，上面整个过程无非就是下面这两步的循环，而循环结束的条件就是最短路径延伸到结束路径即可，也就是我们本例中的D点。

• 第一步：比较已经发展的所有路径，找出目前最短的路径。

• 第二步：在上一步找到的最短路径的基础上发展新的路径，然后重复上一步，直到延伸到end节点为止。

经过这么一分析，在给出具体的代码实现就显得简单多了，我们的程序整体上来说就是一个循环，里边包含着上面这两步。

 

2.具体代码实现

分析完原理后，接下来我们就要开始实现我们的代码了。下方就是我们整个代码的具体实现。当然，我们的图结构是以邻接链表的形式存储的有向联通图。具体代码实现如下所示：

（1）路径结构的存储

我们先创建一个DistanceInfo类，该类中记录了一些距离信息。previousNoteIndex字段存储的是当前节点的前驱节点的索引，默认为-1。而distance存储的就是起始结点到该节点的距离，默认是最大距离。而isInPath则标记该结点是否位于已生成路径的上，如果是的话就是true, 如果不是就是false，默认是false。

　　

 

（2）代码的整体结　　　　

下方代码块就是我们迪杰斯特拉算法代码实现的整体结构。首先我们会创建一个distanceInfos数组，数组中元素的个数就是图的结点的个数。其中存储的是DistanceInfo的对象，每个数组索引对应的DistanceInfo对象中存储的信息就是起始结点到该结点的距离信息。首先我们对起始结点的DistanceInfo对象进行初始化。

紧接着下方这个循环就是我们上面所说的循环，循环结束的条件就是将最短路径延伸到end结点。循环中主要有两步，第一步是在当前循环的index对应的结点上发展新的路径，第二步就是在这些发展的路径中寻找最短路径，在这个新最短路径的基础上再次发展新的路径。

　　

 

（3）发展新的路径

接下来我们来看一下countCurrentNoteAllDistance()方法中的代码，也就是发展新的路径的代码。主要就是遍历邻接链表上当前索引所连的链表上的数据，将这些数据所对应的结点添加到我们的路径上。往路径上添加新的结点是要注意一点，比如A->D是100， 之前B->D是80，如果现在的路径要比之前的路径要大就不更新，反之就更新我们距离信息数组中的DistanceInfo对象。具体代码如下所示：

　　

 

（4）、寻找最小路径

下方代码就是寻找当前已发展的所有路径中最短的那条路径，主要还是对DistanceInfo数组的操作。下方代码，找到最短路径后，并把最短路径的索引进行返回。

　　

上方就是我们迪杰斯特拉算法代码实现的核心代码。

 

三、测试用例

实现完代码后，我们就要对代码进行测试了。下方就是我们的测试用例，该测试用例中创建的图是有向连通图，并且要求出节点A->D的最短路径。

　　

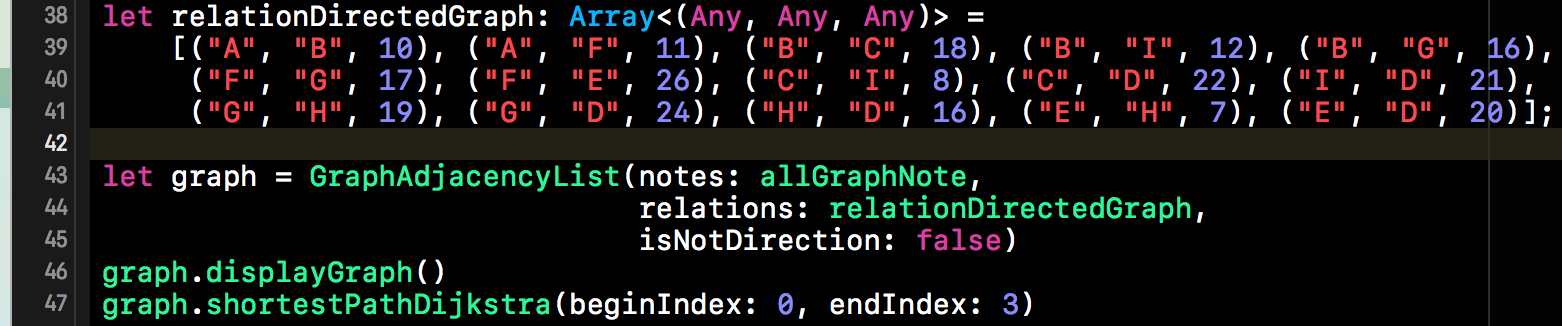
上述测试用例的输入结果如下：

　　

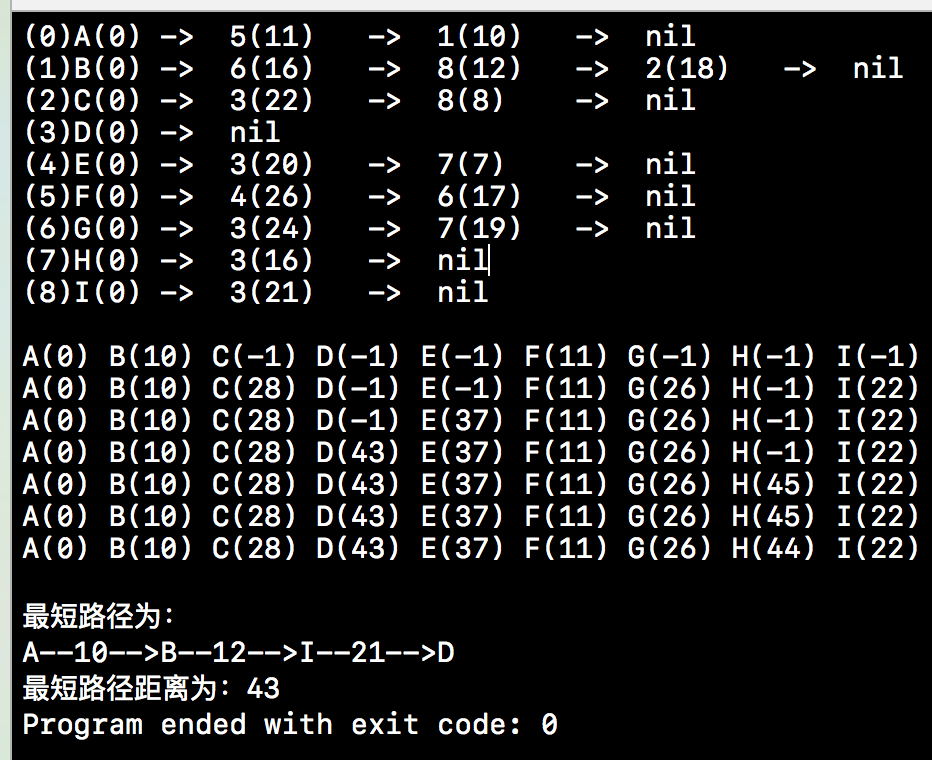
今天的博客就先到这儿，本篇博客所涉及的Demo也将会在github上进行分享，分享地址如下：

github分享地址：https://github.com/lizelu/DataStruct-Swift/tree/master/ShortestPathDijkstra