深度学习笔记03-梯度下降和方向传播

1.梯度下降

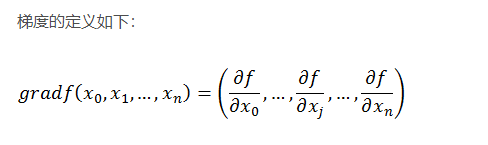
梯度的提出只为回答一个问题：函数在变量空间的某一点处，沿着哪一个方向有最大的变化率？
局部下降最快的方向就是梯度的负方向。

典例：下山问题。

 

假设我们位于黄山的某个山腰处，山势连绵不绝，不知道怎么下山。于是决定走一步算一步，也就是每次沿着当前位置最陡峭最易下山的方向前进一小步，然后继续沿下一个位置最陡方向前进一小步。这样一步一步走下去，一直走到觉得我们已经到了山脚。这里的下山最陡的方向就是梯度的负方向。

梯度下降算法公式：

 

 

推导过程：

一阶泰勒展开式：简单地来说，一阶泰勒展开式利用的就是函数的局部线性近似这个概念。我们以一阶泰勒展开式为例：

 

利用上述的一阶泰勒展开式继续推导：

 

 

 

 

 

 

 

 

2.方向传播

 

求解过程：

先正向，在反向。

(1)正向：

q=-2+5=3,f=q*z=3*(-4)=-12

(2)反向