并查集
并查集
操作:
1.将两个集合合并
2.询问两个元素是否在一个集合里
一.合并集合

示意图:
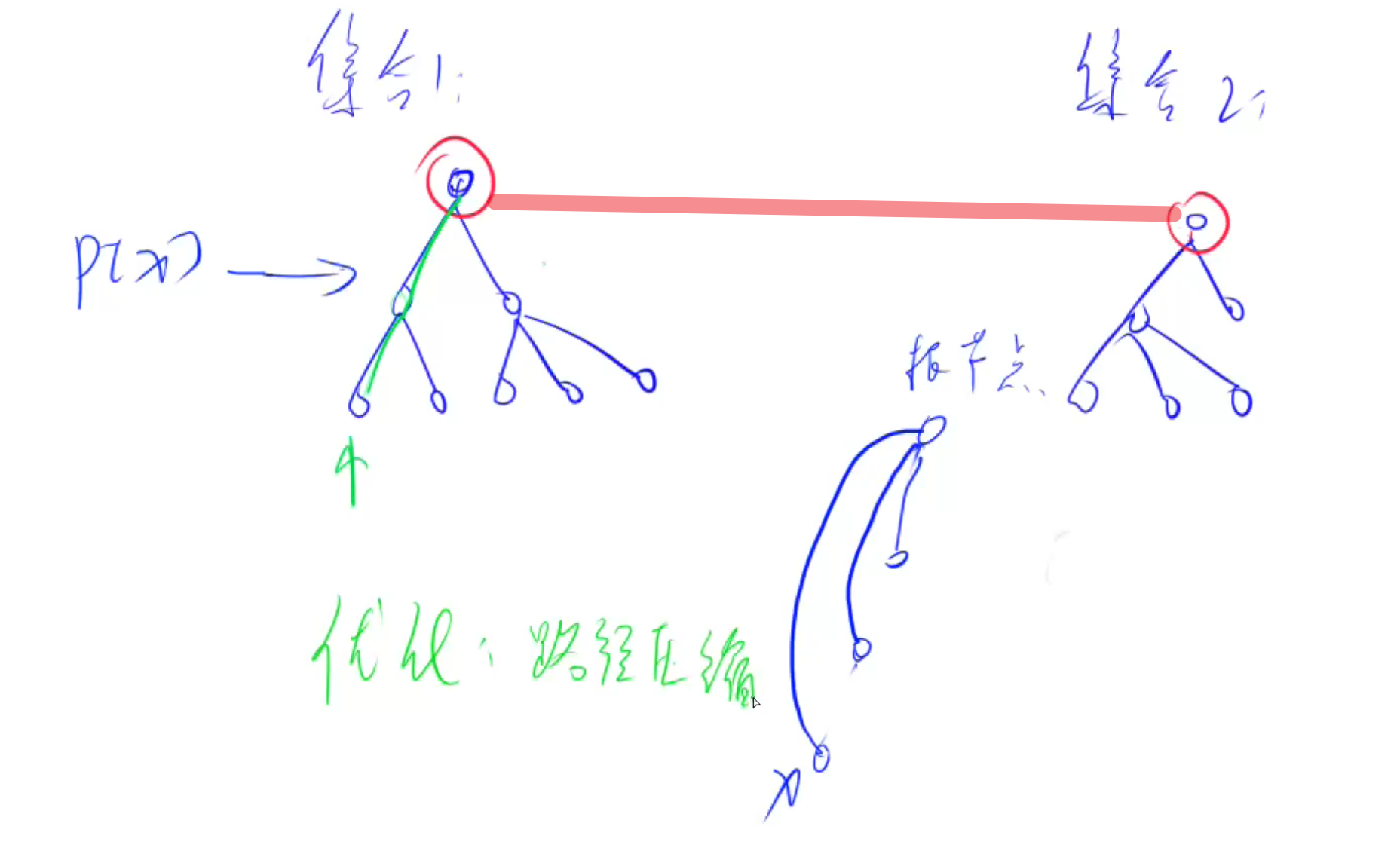
并查集问题的关键:
1.如何判断是否是根节点
p[x]=x就是根节点
2.合并两个集合
将x所在集合接在y集合根节点下面
p[find(x)]=find(y)
find函数表示找该集合的根节点
3.路径压缩
找到根节点的过程中所经过点都指向根节点
p[x]=find(p[x]);
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+8;
int p[N];//p[i]表示i的父节点值
int find(int x) {//找x的根结点
if(p[x]!=x){
p[x]=find(p[x]);//压缩路径
}
return p[x];//根
}
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
p[i]=i;//用点的下标值作为父节点
}
char op;//操作符
int x,y;
while(m--){
cin>>op;
if(op=='M'){
cin>>x>>y;
p[find(x)]=find(y);
}
else if(op=='Q'){
cin>>x>>y;
if(find(x)==find(y)){
cout<<"Yes"<<endl;
}
else {
cout<<"No"<<endl;
}
}
}
return 0;
}二.连通块中点的个数

考点:
并查集:合并集合
记录每个集合内的点数,用根节点下标表示集合
//并查集
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+6;
int cnt[N];//表示根节点为i的集合中结点数
int p[N];//p[i]表示i结点的父节点
//并查集算法
//找根节点
int find(int x) {
//递归
if(p[x]!=x) {
p[x]=find(p[x]) ;
}
return p[x];
}
int main(){
int n,m;
cin>>n>>m;
//开始每个点是单独的集合
for(int i=1;i<=n;i++){
p[i]=i;
cnt[i]=1;
}
string op;
int x,y;
while(m--){
cin>>op;
if(op=="C"){
cin>>x>>y;
int a=find(x);
int b=find(y);
if(a!=b){
p[a]=b;
cnt[b]+=cnt[a];
}
}
else if(op=="Q1"){
cin>>x>>y;
if(find(x)==find(y)){
cout<<"Yes"<<endl;
}
else{
cout<<"No"<<endl;
}
}
else if(op=="Q2"){
cin>>x;
cout<<cnt[find(x)]<<endl;//要先找到该集合的根节点,然后由根节点查询当前集合的点数
}
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号