P6491 [COCI2010-2011#6] ABECEDA

前言

思维难度：绿。

代码难度：绿/蓝。

综合：绿/蓝。

带来两种做法。主要是预处理的部分不同，所以就来水一篇。

传送门。

前置芝士。

分析

我们很容易想到通过输入去确定大概的大小。具体地，对于两字符串，若前 \(i - 1\) 位相同，那么我们要么通过第 \(i\) 位确定大小，要么第 \(i\) 位相同去比较后面。但我们有多个字符串，容易想到，用 vector 存前 \(i - 1\) 位相同的 \(s[j][i]\)。然后根据先后顺序去大致确定粗略的大小。

	for (int i = 0; i < len; i++) {
		string now = "";
		if (v.size()) v.clear();
		for (int j = 1; j <= n; j++) {
			if (s[j].size() < i + 1) continue;//若这一个字符串的大小小于当前枚举的位数，则跳过。
			v2[s[j][i] - 'a'] = 1;//记录在输入中出现过的字母。
			string sub = "";
			for (int k = 0; k < i; k++) sub = sub + s[j][k];
			if (sub != now) {//若前 i - 1 位不同，就进行处理。
				now = sub;
				for (int k = 0; k < (int)v.size() - 1; k++) //注意，一定是 (int)v.size() - 1，而不是 v.size() - 1，具体为什么可自行探究。
					if (v[k] != v[k + 1]) b[v[k] - 'a'][v[k + 1] - 'a'] = 1;//确定大致的大小关系。当然，也有其他写法
				v.clear();
			}
			v.push_back(s[j][i]);//存下当前位，与后面的字母比较
		}
		for (int k = 0; k < (int)v.size() - 1; k++) //最后可能有余下的，也要处理。
			if (v[k] != v[k + 1]) b[v[k] - 'a'][v[k + 1] - 'a'] = 1;
	}

然后若合法，我们这样可以将字典序大的连字典序小连成一个有向无环图，如样例一。

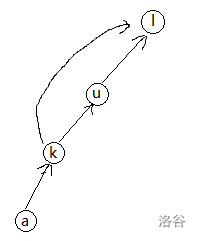
若不合法，就如样例二，会有个环。

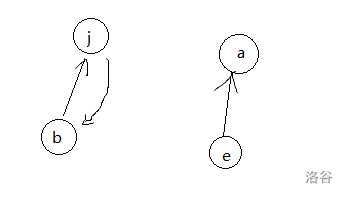
而如果说有多种情况，图是不连通的。

那么，我们就有两种方法去做。

利用 DFS

很容易，若图跑着跑着又回到了起点，那么一定又环，当然，我们不走重复的路，而且我们不用一次走完。然后，我们在走的时候，又可以将途经的点都给做标记，说明这个点小于起点，最终跑到出度为 \(0\) 的点。

void dfs(int now, int x) {
	v1[x] = 1;//标记点到过了。
	if (x != now) b[now][x] = 1;
	for (int i = 0; i < 26; i++) {
		if (b[i][now]) {
			if (i == x) {//到了起点，说明有环。
				cout << '!' << '\n';
				exit(0);
			}
			if (!v1[i]) dfs(i, x);
		}
	}
}

然后我们去找每一个字母字典序大于多少个字母，然后记录下来，最后将记录下来的数组排序。若一个字母字典序大于多少个字母的个数已经有过了，那么就一定不能确定。代码如下。

	for (int i = 0; i < 26; i++) {
		int res = 0;
		memset(v1, 0, sizeof v1);
		dfs(i, i);
		for (int j = 0; j < 26; j++) 
			if (b[j][i]) res++;
		if (v2[i]) a[i].x = ++res;
		a[i].y = char(i + 'a');
		if (v3[res] && res != 0) {
			cout << '?' << '\n';
			return 0;
		}
		v3[res] = 1;
	}
	sort(a, a + 26, cmp);
	for (int i = 0; i < 26; i++) if (a[i].x != 0) cout << a[i].y;

利用拓扑排序

思想很简单。通过他去判环。若队列任意一刻，点的个数大于了 \(1\)，就有可能答案不确定，若有环，则一定有点的入度没减为零。

大佬讲的挺多，可以看一下他们的。我主要讲法一。

代码

法一

#include <bits/stdc++.h>
using namespace std;
 
const int N = 110;
int n, len, d[N];
string s[N];
vector<char> v;
bool b[30][30], v1[N], v2[N], v3[N];
struct node {
	int x;
	char y;
} a[N];
bool cmp(node x, node y) {return x.x < y.x; }
void dfs(int now, int x) {
	v1[x] = 1;
	if (x != now) b[now][x] = 1;
	for (int i = 0; i < 26; i++) {
		if (b[i][now]) {
			if (i == x) {
				cout << '!' << '\n';
				exit(0);
			}
			if (!v1[i]) dfs(i, x);
		}
	}
}
 
int main() {
    // ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> s[i];
	len = 10;
	for (int i = 0; i < len; i++) {
		string now = "";
		if (v.size()) v.clear();
		for (int j = 1; j <= n; j++) {
			if (s[j].size() < i + 1) continue;//若这一个字符串的大小小于当前枚举的位数，则跳过。
			v2[s[j][i] - 'a'] = 1;//记录在输入中出现过的字母。
			string sub = "";
			for (int k = 0; k < i; k++) sub = sub + s[j][k];
			if (sub != now) {//若前 i - 1 位不同，就进行处理。
				now = sub;
				for (int k = 0; k < (int)v.size() - 1; k++) //注意，一定是 (int)v.size() - 1，而不是 v.size() - 1，具体为什么可自行探究。
					if (v[k] != v[k + 1]) b[v[k] - 'a'][v[k + 1] - 'a'] = 1;//确定大致的大小关系。当然，也有其他写法
				v.clear();
			}
			v.push_back(s[j][i]);//存下当前位，与后面的字母比较
		}
		for (int k = 0; k < (int)v.size() - 1; k++) //最后可能有余下的，也要处理。
			if (v[k] != v[k + 1]) b[v[k] - 'a'][v[k + 1] - 'a'] = 1;
	}
	for (int i = 0; i < 26; i++) {
		int res = 0;
		memset(v1, 0, sizeof v1);
		dfs(i, i);
		for (int j = 0; j < 26; j++) 
			if (b[j][i]) res++;
		if (v2[i]) a[i].x = ++res;
		a[i].y = char(i + 'a');
		if (v3[res] && res != 0) {
			cout << '?' << '\n';
			return 0;
		}
		v3[res] = 1;
	}
	sort(a, a + 26, cmp);
	for (int i = 0; i < 26; i++) if (a[i].x != 0) cout << a[i].y;
	return 0;
}

法二

#include <bits/stdc++.h>
using namespace std;
 
const int N = 110;
int n, len, d[N];
string s[N];
vector<char> v;
vector<int> g[N], ans;
 
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> s[i];
	len = 10;
	for (int i = 0; i < len; i++) {
		string now = "";
		if (v.size()) v.clear();
		for (int j = 1; j <= n; j++) {
			if (s[j].size() < i + 1) continue;
			string sub = "";
			for (int k = 0; k < i; k++) sub = sub + s[j][k];
			if (sub != now) {
				now = sub;
				for (int k = 0; k < (int)v.size() - 1; k++) 
					if (v[k] != v[k + 1]) g[(int)v[k] - 'a'].push_back((int)v[k + 1] - (int)'a'), d[v[k + 1] - 'a']++;
                    //这代码换种写法
				v.clear();
			}
			v.push_back(s[j][i]);
		}
		for (int k = 0; k < (int)v.size() - 1; k++) 
			if (v[k] != v[k + 1]) g[v[k] - 'a'].push_back(v[k + 1] - 'a'), d[v[k + 1] - 'a']++;
	}
	queue<int> q;//拓扑
	int f = 0;
	for (int i = 0; i < 26; i++) {
		if (!d[i] && g[i].size()) q.push(i);
	}
	while (q.size()) {
		if (q.size() > 1) f = 1;
		int now = q.front();
		q.pop();
		ans.push_back(now);
		for (int to : g[now]) {
			d[to]--;
			if (!d[to]) q.push(to);
		}
	}
//	cout << d[9];
	for (int i = 0; i < 26; i++) if (d[i]) f = 2;
//	cout << f;
	if (!f) for (int i : ans) cout << char(i + 'a');
	if (f == 2) cout << '!';
	if (f == 1) cout << '?';
	return 0;
}

后记

法一自己想的，法二看了题解。

另外，我想过并查集，但不会，希望有大佬打脸。