11 月杂题记

P7974

注意：花费只跟行有关。

简单的，我们一定是先上升，然后斜着到达 \([l,r]\) 中最大的 \(h_i\) 然后平着走一段，斜着向下，最后垂直向下到达 \(r\)。

如下图：

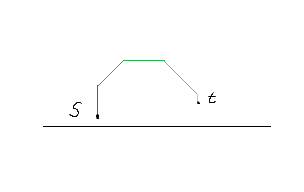
我们可以证明这样是正确的。

问题就在于如何看上升了多少。

可以推出是 \(\max(h_i - (h_l + (i - l)))\)。拆一下就是 \(\max(h_i - i) - (h_l - l)\)。碍于篇幅，就不详细讲了就是懒得写了，没时间（逃。

同理 \(r\) 就是维护 \(\max(h_i + i)\)。

这就是相当于维护三个 St 表。

若:

int g(int l, int r, int op) {
	int len = lg[(r - l + 1)];
	return max(f[op][l][len], f[op][r - (1 << len) + 1][len]);
}

那么答案即为 \(g(s, t, 1) - 4 \times h_s - h_t + 2 \times (g(s, t, 3) + g(s, t, 2))\)。

\(l >= r\) 也就差不多了。

那就只放处理答案和 St 的部分代码了。

for (int j = 1; j <= lg[n]; j++) {
	for (int i = 1; i + (1 << j) - 1 <= n; i++) {
		f[1][i][j] = max(f[1][i][j - 1], f[1][(i + (1 << (j - 1)))][j - 1]);
		f[2][i][j] = max(f[2][i][j - 1], f[2][(i + (1 << (j - 1)))][j - 1]);
		f[3][i][j] = max(f[3][i][j - 1], f[3][(i + (1 << (j - 1)))][j - 1]);
	}
}
while (q--) {
	cin >> s >> t;
	int s1 = s, t1 = t;
	if (t < s) swap(s, t);
	cout << g(s, t, 1) - 4LL * h[s1] - h[t1] + 2LL * (g(s, t, 3) + g(s, t, 2)) << '\n';
}

注意开 long long。

CF543B

我们先设 \(dis[i][j]\) 表示从 \(i\) 到 \(j\) 的路径长度，因为每条边权均为 \(1\) 所以跑 \(n\) 遍 BFS 就出来了。

首先考虑没两条最短路没重叠的情况。显而易见，答案为 \(m - dis[s1][t1] - dis[s2][t2]\)。

再思考有重叠。我们可以枚举重叠的部分，只用枚举重叠部分两端的端点，设为 \(i\) 与 \(j\)。那么，此时答案分两种情况：

\[m - (dis[i][j] + dis[s1][i] + dis[j][t1] + dis[s2][i] + dis[j][t2]) \]

\[m - (dis[i][j] + dis[s1][i] + dis[j][t1] + dis[s2][j] + dis[i][t2]) \]

但是，我们需要判断最短路是否合法。可以自己画图理解一下。

最终答案就是在上面两者取最小值。

主代码：

for (int i = 1; i <= n; i++) BFS(i);
int ans = -dis[s1][t1] - dis[s2][t2] + m;
for (int i = 1; i <= n; i++) {
	for (int j = 1; j <= n; j++) {
		if (dis[s1][i] + dis[i][j] + dis[j][t1] <= l1 && 
           dis[s2][i] + dis[i][j] + dis[j][t2] <= l2)
           ans = max(ans, m - dis[s1][i] - dis[i][j] - dis[j][t1] - dis[s2][i] - dis[j][t2]);
		if (dis[s1][j] + dis[j][i] + dis[i][t1] <= l1 && 
           dis[s2][i] + dis[i][j] + dis[j][t2] <= l2) 
           ans = max(ans, m - dis[s1][j] - dis[i][j] - dis[i][t1] - dis[s2][i] - dis[j][t2]);
	}
}
if (dis[s1][t1] > l1 || dis[s2][t2] > l2) cout << -1;
else cout << ans;