CF755F
前言
随机跳题跳来的。本来以为很简单，结果花了我这个蒟蒻三个多小时。果然还是太蒻了呀。还有题目中的拖拉机是什么呀？
于是，题解记之。
题意
分析
我们容易发现，若把每个人当做一个点，那么给人送礼物，则是向这个人连一条边。
看不懂？直接上图！
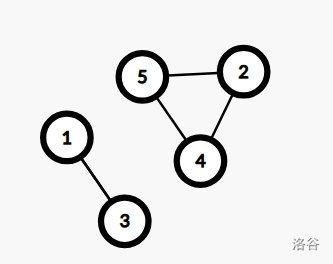
上图表示的是：
5 2
3 4 1 5 2
这一组数据。当然有向或无向都对这题没有影响。
根据观察，容易得出，这个图是由若干个环组成的，并且，环的个数也就是连通块的个数。
那么，我们便可以处理出环的个数，与他所包含的点的个数，也就是人的个数。
inline int dfs(int x) {//处理出环的中有多少个点。
v[x] = 1;
if (v[p[x]]) return 1;
return dfs(p[x]) + 1;
}
for (int i = 1; i <= n; i++)//处理有多少个环（连通块）
if (!v[i]) cnt[++len] = dfs(i);
最大值
最大值相对于最小值会简单一点。
我们想一想很容易得出，若是有一个人没有礼物，那么他要给的对象与他自己都没有礼物。为避免思维僵化，请读者自行证明。
那么，我们便可以分奇数环与偶数换来讨论。设环中点的数量为 \(x\)。
- 偶数个。那么就可以分成 \(\frac{k}{2}\) 组，使每一组任意一个人没带，则他要给的对象与他自己都没有礼物。
- 奇数个。那么就可以分成 \(\lfloor \frac{k}{2} \rfloor\) 组与多出来的一个人。
若 \(\sum \lfloor \frac{c[i]}{2} \rfloor \ge k\)，那么，答案即为 \(k \times 2\)。否则我们就将 \(\sum \lfloor \frac{c[i]}{2} \rfloor \ge k\) 加上，然后再在奇数环中找多出来的一个数，直至加到大于 \(k\) 或 人数等于 \(n\) 时停止。
最小值
刚开始，我也觉得这是贪心，直至我 WA 了不知道多少次，想通了，这是个 DP ！！！
在这里，给组对于贪心的 hack。
输入：
10 7
9 6 2 8 1 3 10 4 5 7
输出：
7 10
如下图。
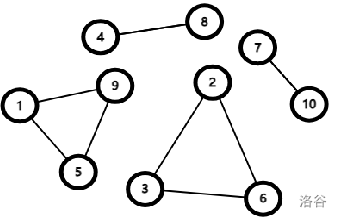
容易的，我们可以想出，尽量使一整个环内的人不带礼物。
略微证明一下：
设有一个环内都是没带礼物的人，人数为 \(x\)，另一个环都带了礼物，剩下的环保持不变，且人数大于一。那么这两个环内一共就有 \(x\) 人没有礼物，但是当这个环有了一个人带了礼物，因为总共没带礼物的人数相同，那么两个环分别就有 \(x - 1\) 与 \(1\) 个人没带礼物，根据最大值那里的推论，总共就有 \(x + 2\) 个人没有礼物。
那么，也就是说，我们需要使这 \(len\) 个环中，抽出几个环，若他们人数总值等于 \(k\)，那么肯定是最少有 \(k\) 个人没有礼物，若不等于有 \(k + 1\) 人。请读者自行思考为什么。但是我还是会说的。
根据上述内容可以得出若他们人数总值等于 \(k\)，那么肯定是最少有 \(k\) 个人没有礼物。
若要使有 \(k + 1\) 个人没有礼物，则使没有礼物的人都不得到礼物。但是，我们肯定会多出来一个人不能给没有礼物的人礼物，则有一个带了礼物的人没有送来的礼物。
有点绕，自行理解一下，当然，看不懂，是我的问题。
显然就考虑背包 DP。
for (int i = 1; i <= len; i++)
for (int j = k; j >= cnt[i]; j--)
f[j] |= f[j - cnt[i]];
\(f[i]\) 表示能不能用若干个环组合出 \(i\) 个人没带礼物。
时间复杂度 \(O(n \times m)\)。肯定会爆，考虑优化。
我们可以知道大多数的环中的人的数量是相同的。那么这题就转化成了多重背包，我们就可以用二进制优化。
inline void fen(int x, int v) {二进制优化
for (int i = 1; x > 0; i <<= 1) {
int j = min(i, x);
a[++l] = j * v;
x -= j;
}
}
时间复杂度就降下来了。可以过。
Code
我代码写得太差了，建议大家参考其他题解的代码。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
int n, p[N], cnt[N], len, k, ans;
int c[N], l, a[N], mx, f[N * 10];//f 开 1e7 是因为二进制拆分会产生 nlogn 个数。但到不了极限。
bool v[N];
inline int dfs(int x) {//处理出环的中有多少个点。
v[x] = 1;
if (v[p[x]]) return 1;
return dfs(p[x]) + 1;
}
inline void fen(int x, int v) {二进制优化
for (int i = 1; x > 0; i <<= 1) {
int j = min(i, x);
a[++l] = j * v;
x -= j;
}
}
int main() {
ios::sync_with_stdio(0);
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> p[i];
for (int i = 1; i <= n; i++)//处理有多少个环（连通块）
if (!v[i]) cnt[++len] = dfs(i), c[cnt[len]]++;
sort(cnt + 1, cnt + 1 + len);//最大值需要
for (int i = 1; i <= n; i++) if (c[i]) fen(c[i], i);
f[0] = 1;
for (int i = 1; i <= l; i++)
for (int j = k; j >= a[i]; j--)
f[j] |= f[j - a[i]];
int kk = k;
if (!f[k]) cout << k + 1 << ' ';
else cout << k << ' ';//最小值
ans = 0;
for (int i = len; i > 0; i--) {
if (cnt[i] <= kk * 2) {
if (cnt[i] & 1) ans += cnt[i] - 1, kk -= cnt[i] / 2, cnt[i] = 1;
else ans += cnt[i], kk -= cnt[i] / 2, cnt[i] = 0;
}
else {//排序的原因，这样就可以提前 break。
ans += kk * 2;
kk = 0;
break;
}
if (!kk) break;
}
for (int i = 1; i <= len; i++) {//处理奇数环
if (!kk) {
break;
}
else {
kk -= cnt[i];
ans += cnt[i];
}
}
cout << min(ans, n);
return 0;
}
后记
本蒟蒻写过的最长的一篇题解吧。
在本人退役前或有空会来解答问题。
