Educational Codeforces Round 166 (Rated for Div. 2)
写在前面
比赛地址:https://codeforces.com/contest/1976
满课,并且 48 小时之内只睡了 8h。
本来不想打的,但是手痒就上小号打了,然而唐唐唐掉大分呃呃
A
签到。
感谢 isdigit 函数。
//
/*
By:Luckyblock
*/
#include <bits/stdc++.h>
#define LL long long
//=============================================================
//=============================================================
//=============================================================
int main() {
//freopen("1.txt", "r", stdin);
std::ios::sync_with_stdio(0), std::cin.tie(0);
int T; std::cin >> T;
while (T --) {
int n; std::cin >> n;
std::string s; std::cin >> s;
int flag = 1;
for (int i = 1; i < n; ++ i) {
if (!isdigit(s[i - 1]) && isdigit(s[i])) flag = 0;
}
for (int i = 0, lst = -1; i < n; ++ i) {
if (isdigit(s[i])) {
if (lst == -1) lst = i;
else if (s[lst] > s[i]) flag = 0;
lst = i;
}
}
for (int i = 0, lst = -1; i < n; ++ i) {
if (!isdigit(s[i])) {
if (lst == -1) lst = i;
else if (s[lst] > s[i]) flag = 0;
lst = i;
}
}
std::cout << (flag ? "YES\n" : "NO\n");
}
return 0;
}
B
模拟。
对 \(a_1\sim a_n\) 的调整的代价是固定的,即为 \(\sum_{1\le i\le n} |a_i - b_i|\)。在对它们调整的过程中需要选择一个数复制一份变为 \(a_{n + 1}\),并最小化调整 \(a_{n + 1}\) 至 \(b_{n + 1}\) 的代价 \(|b_{n + 1} - a_{n + 1}|\)。
若存在 \(1\le i\le n\),使得 \(\min(a_i, b_i) \le b_{n + 1}\le \max(a_i, b_i)\),则 \(|b_{n + 1} - a_{n + 1}|\) 的值可以为 0;否则选择的被复制的数一定在集合 \(\{a_i\} \cup\{b_i\}\) 中,选择其中与 \(b_{n + 1}\) 最接近的数复制并计算代价即可。
//
/*
By:Luckyblock
*/
#include <bits/stdc++.h>
#define LL long long
const int kN = 2e5 + 10;
//=============================================================
int n, a[kN], b[kN];
//=============================================================
//=============================================================
int main() {
//freopen("1.txt", "r", stdin);
std::ios::sync_with_stdio(0), std::cin.tie(0);
int T; std::cin >> T;
while (T --) {
std::cin >> n;
for (int i = 1; i <= n; ++ i) std::cin >> a[i];
for (int i = 1; i <= n + 1; ++ i) std::cin >> b[i];
LL ans = 0, flag = 0;
for (int i = 1; i <= n; ++ i) {
ans += abs(a[i] - b[i]);
if (std::min(a[i], b[i]) <= b[n + 1] && b[n + 1] <= std::max(a[i], b[i])) flag = 1;
}
if (!flag) {
LL delta = 1e9;
for (int i = 1; i <= n; ++ i) {
delta = std::min(delta, 1ll * abs(b[n + 1] - a[i]));
delta = std::min(delta, 1ll * abs(b[n + 1] - b[i]));
}
ans += delta;
}
std::cout << ans + 1 << "\n";
}
return 0;
}
C
排序。
读错题了唐唐唐唐唐——获得了一道新题哈哈,什么时候需要就放上去。
首先假设 \(n + m + 1\) 个人全部到来,按照题意进行模拟找到其较优岗位并求得贡献之和。
然后按照到来顺序,分别枚举每个岗位中的人 \(i\),记该岗位人数上限为 \(k\):
- 若这个人之前已经有 \(k\) 个人入职该岗位,则这个人不来贡献仅减少 \(\min(a_i, b_i)\)。
- 若这个人之前不到 \(k\) 个人入职该岗位,且以该岗位为较优岗位的人总数不大于 \(k\) 个,则这个人不来贡献减少 \(\max(a_i, b_i)\)。
- 否则这个不来一定会使得第 \(k\) 个人入职该岗位,则贡献变化量为 \(-\max(a_i, b_i) + \max(a_{k}, b_{k}) - \min(a_k, b_k)\)。
讨论即可,总时间复杂度 \(O(n+m)\) 级别。
//
/*
By:Luckyblock
*/
#include <bits/stdc++.h>
#define LL long long
#define pii std::pair<int,int>
#define mp std::make_pair
const int kN = 2e5 + 10;
//=============================================================
int n, m;
LL sum, ans[kN];
std::vector<int> aa, bb;
int a[kN], b[kN], c[kN];
//=============================================================
//=============================================================
int main() {
// freopen("1.txt", "r", stdin);
std::ios::sync_with_stdio(0), std::cin.tie(0);
int T; std::cin >> T;
while (T --) {
std::cin >> n >> m;
sum = 0;
aa.clear(), bb.clear();
for (int i = 1; i <= n + m + 1; ++ i) std::cin >> a[i];
for (int i = 1; i <= n + m + 1; ++ i) {
std::cin >> b[i];
c[i] = abs(a[i] - b[i]);
sum += std::min(a[i], b[i]);
}
int cnta = 0, cntb = 0;
for (int i = 1; i <= n + m + 1; ++ i) {
if (a[i] > b[i]) {
++ cnta;
if (cnta <= n) sum += a[i] - b[i];
aa.push_back(i);
} else {
++ cntb;
if (cntb <= m) sum += b[i] - a[i];
bb.push_back(i);
}
}
for (int i = aa.size() - 1; i >= n; -- i) ans[aa[i]] = sum - b[aa[i]];
if ((int) aa.size() <= n) {
for (int i = 0; i < (int) aa.size(); ++ i) ans[aa[i]] = sum - a[aa[i]];
} else {
for (int i = n - 1; i >= 0; -- i) ans[aa[i]] = sum - a[aa[i]] + c[aa[n]];
}
for (int i = bb.size() - 1; i >= m; -- i) ans[bb[i]] = sum - a[bb[i]];
if ((int) bb.size() <= m) {
for (int i = 0; i < (int) bb.size(); ++ i) ans[bb[i]] = sum - b[bb[i]];
} else {
for (int i = m - 1; i >= 0; -- i) ans[bb[i]] = sum - b[bb[i]] + c[bb[m]];
}
for (int i = 1; i <= n + m + 1; ++ i) std::cout << ans[i] << " ";
std::cout << "\n";
}
return 0;
}
D
括号序列,枚举。
好玩题,场上一直想着怎么拆成两半拼起来了,还能这么想的 oonp。
首先考虑如果选出了一段区间 \([l, r]\) 并将其逐字符取反,如何判断取反后整个括号序列是否合法。一个显然的想法是将 \([1, l - 1]\),\([l, r]\),\([r + 1, n]\) 三段括号串分别先进行括号匹配将它们化简,然后检查化简后的三段能否匹配。套路地考虑将左右括号分别看做 \(\plusmn 1\),以 (()())(()) 为例则有如下的折线图:
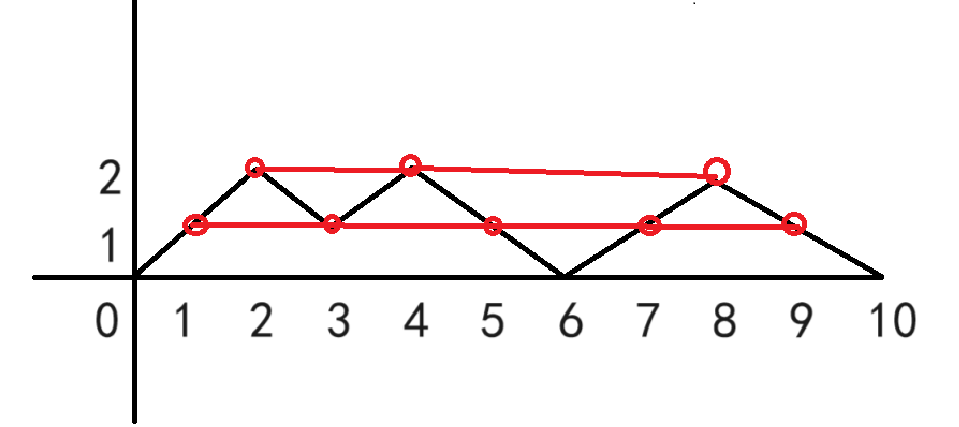
发现区间 \([l, r]\) 取反相当于将选中的折线 \((l - 1)\rightarrow r\) 中各段进行翻折。为了保证翻折后折线仍然是连续的,且不会翻折到 \(x\) 轴下方,记位置 \(i\) 处折线高度为 \(h_i\),则需要满足:
上述 \(h\) 数组可以在括号匹配过程中直接求得,则一个显然的想法是按照值递减枚举 \(h_{l - 1} = h_r\),再顺序枚举对应的每个位置,然后考虑每个位置与之前多少位置可以构成合法的修改区间。发现仅需检查其中是否有不满足条件 2 的位置即可,考虑双指针枚举 \(\ge 2\times h_{l - 1}\) 的所有位置并使用 set 记录,求合法位置对时同样双指针求得满足条件 2 的位置的合法对即可。
总时间复杂度 \(O(n\log n)\) 级别。
//
/*
By:Luckyblock
*/
#include <bits/stdc++.h>
#define LL long long
const int kN = 2e5 + 10;
int n, pre[kN];
std::string s;
LL ans;
std::vector<int> pos[kN];
std::set<int> high;
void solve() {
n = s.length();
high.clear();
for (int i = 0; i < n; ++ i) {
pre[i + 1] = pre[i] + (s[i] == '(' ? 1 : -1);
pos[i + 1].clear();
}
for (int i = 1; i <= n; ++ i) pos[pre[i]].push_back(i);
for (int i = n, j = n; i; -- i) {
while (j > 2 * i) {
for (auto p: pos[j]) high.insert(p);
-- j;
}
for (int k = 1, sz = pos[i].size(), cnt = 1; k < sz; ++ k) {
auto it = high.upper_bound(pos[i][k - 1]);
if (it == high.end() || *it > pos[i][k]) {
ans += cnt;
} else {
cnt = 0;
}
++ cnt;
}
}
}
int main() {
int T; std::cin >> T;
while (T --) {
std::cin >> s;
ans = 0;
solve();
std::cout << ans << "\n";
}
}
/*
1
()()()()
1
()((()))
10123210
(()(()))
()(()())
*/
E
写在最后
参考:
学到了什么:
- D:括号序列的又一种数形结合的模型转换。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号