P4919 Marisa采蘑菇

知识点：扫描线，树状数组

原题面：Luogu

更好的阅读体验：My blog。

最后扯一句，魔理沙世界第一可爱.jpg ^[1]

简述

给定一长度为 \(n\) 的数列 \(a\)，参数 \(k\)。给定 \(m\) 次询问。
每次询问给定区间 \([l,r]\)，求区间内有多少个数，满足在区间内的出现次数与区间外的出现次数之差小于等于给定的常数 \(k\)。
\(1\le n,m\le 10^6\)，\(0\le k\le 10^4\)，\(0\le l\le r\le n\)。
3S，128MB。

分析

对于一个询问区间 \([l,r]\)，设 \(s\) 为权值 \(x\) 在整个数列中出现的次数。考虑某种权值 \(x\) 对该区间有贡献的条件，显然为 \(|(s - x) - x|\le k\)。上式解得：

\[s - k\le 2\cdot x\le s + k \]

考虑离线询问并排序，通过对询问进行扫描线固定询问的右端点。考虑在询问右端点单调右移的同时，对于每种权值，都维护它有所贡献的询问的左端点范围 \([L,R]\)。当询问的左端点 \(l\in [L,R]\) 时，区间 \([l,r]\) 内这种权值出现次数满足上式。右端点右移到下一个同权值位置时更新区间。如下图所示：

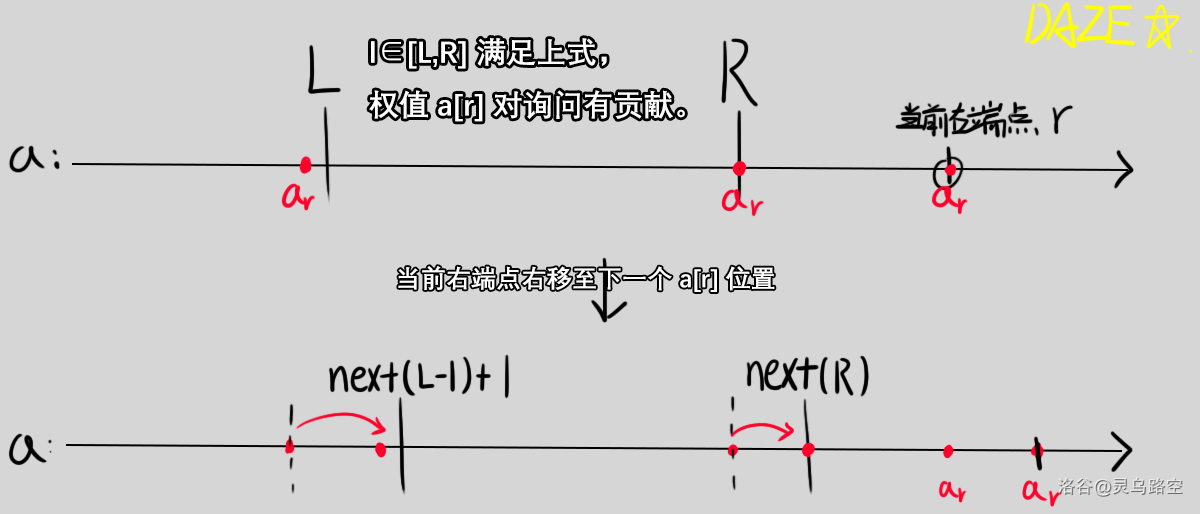
当前缀 \([1,r]\) 中某权值出现次数满足上式时，有贡献的区间是数列的一段完整前缀，且需要注意 \(L,R\) 的初始取值，详见代码。

当扫描线枚举的右端点为 \(r\)，维护上述信息后，询问 \([l,r]\) 的答案即为覆盖了左端点 \(l\) 的区间的个数。
发现上述算法需要支持区间修改，单点求和，树状数组维护即可，总复杂度 \(O(m\log m + (n+m)\log n)\) 级别。

代码

//知识点：扫描线，树状数组
/*
By:Luckyblock
*/
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#define LL long long
const int kN = 1e6 + 10;
//=============================================================
struct Q {
  int l, r, id;
} q[kN];
int n, m, k, col[kN], ans[kN];
int last[kN], ne[kN], first[kN], sum[kN];
//ne[i]：col[i] 之后第一个等于 col[i] 的位置
//first[i]：颜色 i 在数列中第一次出现的位置
//sum[i]：颜色 i 在数列中出现次数之和
int cnt[kN], L[kN], R[kN];
//在扫描线过程中维护，cnt[i]：到扫描位置为止 i 的出现次数
//L[i]~R[i]：当前扫描位置作为询问右端点时，颜色 i 有贡献的询问左端点范围
//=============================================================
inline int read() {
  int f = 1, w = 0;
  char ch = getchar();
  for (; !isdigit(ch); ch = getchar())
    if (ch == '-') f = -1;
  for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
  return f * w;
}
void Chkmax(int &fir, int sec) {
  if (sec > fir) fir = sec;
}
void Chkmin(int &fir, int sec) {
  if (sec < fir) fir = sec;
}
bool CMP(Q fir_, Q sec_) {
  if (fir_.r != sec_.r) return fir_.r < sec_.r;
  return fir_.l < sec_.l;
}
namespace Bit {
  #define low(x) (x&-x)
  const int kLim = 1e6;
  int t[kLim + 10];
  void Add(int pos_, int val_) {
    ++ pos_;
    for (int i = pos_; i <= kLim; i += low(i)) t[i] += val_;
  }
  int Sum(int pos_) {
    ++ pos_;
    int ret = 0;
    for (int i = pos_; i; i -= low(i)) ret += t[i];
    return ret;
  }
  void Modify(int l_, int r_, int val_) {
    Add(l_, val_);
    Add(r_ + 1, -val_);
  }
}
void Init() {
  n = read(), m = read(), k = read();
  for (int i = 1; i <= n; ++ i) {
    col[i] = read();
    if (++ sum[col[i]] == 1) first[col[i]] = i;
    last[col[i]] = n;
  }
  for (int i = n; i >= 1; -- i) {
    ne[i] = last[col[i]];
    last[col[i]] = i;
  }
  for (int i = 1; i <= m; ++ i) q[i] = (Q) {read(), read(), i};
  std::sort(q + 1, q + m + 1, CMP);
}
void Modify(int pos_) {
  int c = col[pos_], s = sum[c];
  ++ cnt[c];
  if (R[c]) Bit::Modify(L[c], R[c], -1); //减去之前颜色 i 对询问左端点的贡献
  if (2 * cnt[c] >= s - k) R[c] = R[c] ? ne[R[c]] : first[c]; //右端点左移，增加区间内该权值出现次数。
  if (2 * cnt[c] > s + k) L[c] = L[c] ?  ne[L[c] - 1] + 1 : first[c] + 1; //左端点右移，减小区间内该权值出现次数。注意开区间。
  if (R[c]) Bit::Modify(L[c], R[c], 1);
}
//=============================================================
int main() { 
  Init();
  for (int i = 1, nowr = 0; i <= m; ++ i) {
    while (nowr < q[i].r && nowr < n) Modify(++ nowr); //扫描位置更新
    ans[q[i].id] = Bit::Sum(q[i].l);
  }
  for (int i = 1; i <= m; ++ i) printf("%d\n", ans[i]);
  return 0; 
}

---

1. https://www.zhihu.com/question/58000296/answer/244087811 ↩︎