Codeforces Round #676

写在前面
A
B
C
D
E
总结

写在前面

比赛地址：https://codeforces.com/contest/1421。

打到一半就去吃饭的第一场 CF。

A

\(T\) 组数据，每次给定正整数 \(a,b\)，求一个正整数 \(x\)，满足 \((a \oplus x)+(b \oplus x)\) 最小。
求该最小值。
\(1\le T\le 10^4\)，\(1\le a,b\le 10^9\)。
1S，256MB。

若 \(a,b\) 某位上均为 1，则 \(x\) 该位为 1 时，可令 \(a \oplus x,b \oplus x\) 该位均为 0，从而使最终的值更小。
若 \(a,b\) 某位上均为 0，\(x\) 该位应为 0，原理同上。
若 \(a,b\) 某位不同，\(x\) 的该位可任意取， \(a \oplus x\)，\(b \oplus x\) 该位均为 1。

则显然 \(\min\{(a \oplus x)+(b \oplus x)\} = a\oplus b\)。

//知识点：二进制
/*
By:Luckyblock
*/
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#define LL long long
//=============================================================
LL T, a, b;
//=============================================================
inline LL read() {
  LL f = 1, w = 0;
  char ch = getchar();
  for (; !isdigit(ch); ch = getchar())
    if (ch == '-') f = -1;
  for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
  return f * w;
}
void Chkmax(int &fir_, int sec_) {
  if (sec_ > fir_) fir_ = sec_;
}
void Chkmin(int &fir_, int sec_) {
  if (sec_ < fir_) fir_ = sec_;
}
//=============================================================
int main() {
  T = read();
  while (T --) {
    a = read(), b = read(), ans = 0ll;
    printf("%lld\n", a ^ b);
  }
  return 0;
}

B

一个人，可以从 \((1,1)\)开始，四联通地向与自己脚下格子数字(0 或 1) 相同的格子移动，最终要到达 \((n,n)\)。
起始时的数字可以是 0 或 1。
你需要输出一种修改方案，修改 \(c\) 个点的数字，使得这个人无法从 \((1,1)\) 走到 \((n,n)\)，并输出方案。
\(3\leq n\leq 100\)，\(0\leq c\leq 2\)。
1S，256MB。

显然只会改与 \((1,1)\) 相邻的两个格子，和与 \((n,n)\) 相邻的两个格子。
暴力枚举这四个位置判断即可。

//知识点：暴力
/*
By:Luckyblock
*/
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#define LL long long
const int kMaxn = 210;
//=============================================================
int T, n, ans_num, ansx[kMaxn], ansy[kMaxn];
bool map[kMaxn][kMaxn];
char s[kMaxn];
//=============================================================
inline int read() {
  int f = 1, w = 0;
  char ch = getchar();
  for (; !isdigit(ch); ch = getchar())
    if (ch == '-') f = -1;
  for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
  return f * w;
}
void Chkmax(int &fir_, int sec_) {
  if (sec_ > fir_) fir_ = sec_;
}
void Chkmin(int &fir_, int sec_) {
  if (sec_ < fir_) fir_ = sec_;
}
//=============================================================
int main() {
  T = read();
  while (T --) {
    n = read();
    for (int i = 1; i <= n; ++ i) { 
      scanf("%s", s + 1);
      for (int j = 1; j <= n; ++ j) {
        if (s[j] == '0') map[i][j] = false;
        else if (s[j] == '1') map[i][j] = true;
      }
    }
    
    if (map[1][2] == map[2][1]) {
      if (map[n - 1][n] == map[n][n - 1]) {
        if (map[1][2] != map[n][n - 1]) {
          ans_num = 0; 
        } else {
          ans_num = 2; 
          ansx[1] = 1;
          ansy[1] = 2;
          ansx[2] = 2;
          ansy[2] = 1;
        }
      } else {
        if (map[n - 1][n] == map[1][2]) {
          ans_num = 1;
          ansx[1] = n - 1;
          ansy[1] = n;
        } else {
          ans_num = 1;
          ansx[1] = n;
          ansy[1] = n - 1;
        }
      }
    } else {
      if (map[n - 1][n] == map[n][n - 1]) {
        if (map[n - 1][n] == map[1][2]) {
          ans_num = 1;
          ansx[1] = 1;
          ansy[1] = 2;
        } else {
          ans_num = 1;
          ansx[1] = 2;
          ansy[1] = 1;
        }
      } else {
        ans_num = 2;
        if (map[1][2] == 1) {
          ansx[1] = 1;
          ansy[1] = 2;
        } else {
          ansx[1] = 2;
          ansy[1] = 1;
        }
        if (map[n - 1][n] == 0) {
          ansx[2] = n - 1;
          ansy[2] = n;
        } else {
          ansx[2] = n;
          ansy[2] = n - 1;
        }
      }
    }
    
    printf("%d\n", ans_num);
    for (int i = 1; i <= ans_num; ++ i) {
      printf("%d %d\n", ansx[i], ansy[i]);
    }
    printf("\n");
  }
  return 0;
}

C

给定一下标从 \(1\) 开始的字符串 \(s\)，每次可以选择一个位置 \(i(2\le i\le n-1)\)，选择进行下列两种操作之一：

将翻转后的子串 \(s_2s_3\cdots s_i\) 接在字符串 \(s\) 的头部。

将翻转后子串 \(s_is_{i+1}\cdots s_{n-1}\) 翻转后接在字符串 \(s\) 的尾部。

要求构造一种操作次数 \(\le 30\) 的方案，使得 \(s\) 变成回文串。
\(3\le |s|\le 10^5\)。
1S，256MB。

考虑所有字符均不同的一般情况，YY 了一种奇怪的方法过了。
令 \(n\) 为当前字符串的长度，有下列构造方法：

把 \(s_2\) 放到头部。
把 \(s_2\sim s_{n}\) 放到尾部。
把 \(s_{n-1}\) 放到尾部。

大概长这样：

\[\texttt{abcde}\rightarrow \texttt{babcde}\rightarrow \texttt{babcdedcba}\rightarrow \texttt{babcdedcbab} \]

思考下原理：

使得 \(s_1\sim s_3\) 回文。
使得 \(s_2\sim s_{n}\) 回文。
此时 \(s\) 与回文只差 \(s_1\) 这一个字符，进行了第 1 次操作，字符 \(s_1\) 即为 \(s_{n-1}\)，于是把 \(s_{n-1}\) 放到尾部即可。

//知识点：构造
/*
By:Luckyblock
*/
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#include <string>
#include <iostream>
#define LL long long
//=============================================================
int n, flag = 1;
std::string s;
//=============================================================
inline int read() {
  int f = 1, w = 0;
  char ch = getchar();
  for (; !isdigit(ch); ch = getchar())
    if (ch == '-') f = -1;
  for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
  return f * w;
}
void Chkmax(int &fir, int sec) {
  if (sec > fir) fir = sec;
}
void Chkmin(int &fir, int sec) {
  if (sec < fir) fir = sec;
}
//=============================================================
int main() { 
  std::cin >> s;
  n = s.length();
  printf("3\n");
  printf("L %d\n", 2);
  ++ n;
  printf("R %d\n", 2);
  n += (n - 2);
  printf("R %d\n", n - 1);
  return 0; 
}

D

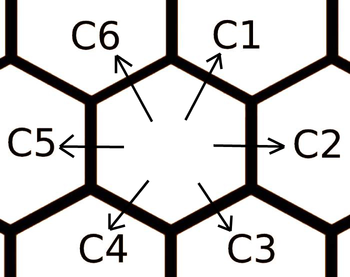
给定一如图一所示的图，初始位置为 \((0,0)\)。
每次可以往图二所示 6 个方向走，代价分别为 \(c_1\sim c_6\)。
\(t\) 组数据，每次求走到给定坐标 \((x,y)\) 的最小代价。
\(1\le t\le 10^4\)，\(-10^9\le x,y\le 10^9\)，\(1\le c_i\le 10^9\)。
2S，256MB。

考虑建图跑最短路？数据范围比较神奇，图建不下，考虑 \(O(1)\) 算法。
发现题目给每一个位置都分配了一个二维坐标，考虑把这个六边形图放到直角坐标系里，有如下形式：

注意新图的 \((x,y)\) 与原图的 \((x,y)\) 是反的。
发现向 \(1\) 方向走，可被替换成先向 \(2\) 再向 \(6\) 走。其他方向同理。
于是先大力迭代先求得向每个方向走 1 步的最小代价。

又每次的移动距离均为 1，于是可以分象限讨论：

当 \((x,y)\) 位于第二四象限时，只能沿与坐标轴平行方向走，答案可直接算出。
当 \((x,y)\) 位于第一象限时，一定是先走 \(c_1\)，再走 \(c_2/c_6\)。
因为之前已经确定了走各步的最小代价，迭代后的 \(c_1\) 已经考虑过先走 \(c_2 + c_6\) 的情况了。
当 \((x,y)\) 位于第三象限时，同理，先走 \(c_4\)，再走 \(c_3/c_5\)。

各种情况均可 \(O(1)\) 算出答案。

//知识点：暴力，图论
/*
By:Luckyblock
*/
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#define LL long long
//=============================================================
LL ans, c[7];
bool flag;
//=============================================================
inline int read() {
  int f = 1, w = 0;
  char ch = getchar();
  for (; !isdigit(ch); ch = getchar())
    if (ch == '-') f = -1;
  for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
  return f * w;
}
void Chkmax(int &fir, int sec) {
  if (sec > fir) fir = sec;
}
void Chkmin(LL &fir, LL sec) {
  if (sec < fir) {
    fir = sec;
    flag = false;
  }
}
//=============================================================
int main() { 
  int t = read();
  while (t --) {
    LL y = read(), x = read();
    for (int i = 1; i <= 6; ++ i) c[i] = read();
    while (1) {
      flag = true;
      Chkmin(c[1], c[2] + c[6]);
      Chkmin(c[2], c[1] + c[3]);
      Chkmin(c[3], c[2] + c[4]);
      Chkmin(c[4], c[3] + c[5]);
      Chkmin(c[5], c[4] + c[6]);
      Chkmin(c[6], c[1] + c[5]);
      if (flag) break;
    }
    
    if (x >= 0 && y >= 0) {
      ans = std::min(x, y) * c[1];
      ans += x >= y ? (x - y) * c[2] : (y - x) * c[6];
    } else if (x >= 0 && y <= 0) {
      y = -y;
      ans = x * c[2] + y * c[3];
    } else if (x <= 0 && y >= 0) {
      x = -x;
      ans = x * c[5] + y * c[6];
    } else if (x <= 0 && y <= 0) {
      x = -x, y = -y;
      ans = std::min(x, y) * c[4];
      ans += x >= y ? (x - y) * c[5] : (y - x) * c[3];
    }
    printf("%lld\n", ans);
  }
  return 0; 
}

E

给定一数列 \(a\)，每次可以选择两个相邻的数 \(a_i,a_{i+1}\) 合并成一个数，新的数为 \(-(a_i+a_{i+1})\)。
求合并到只剩一个数时，剩下的数的最大值。
\(1\le n\le 2\times 10^5\)，\(|a_i|\le 10^9\)。
2S，256MB。

奇怪的找规律题。

若两个数合并，贡献形式可以写成 \(-a_i - a_{i+1}\)。
若有三个数，先后合并两次，贡献呈现 \(-a_i + a_{i+1} + a_{i+2}\) 的形式。
由此抽象一下题意，题目实际上要求对数列 \(a\) 每个位置都分配一个 \(+/-\)，某些分配方案不合法。再将分配后得到的数列求和，求最大的和。

考虑什么样的分配方案不合法。
若分配方案呈现 \(+/-\) 交替，则一定不合法。因为第一次合并时必然使两个位置的符号相同。

然后写个爆搜找下规律：

//我是一个可以输出 输出合并方案 的暴力。
/*
By:Luckyblock
*/
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#include <vector>
#define LL long long
const LL kInf = 1e15 + 2077;
const int kN = 2e5 + 10;
//=============================================================
int n, a[kN];
LL ans = -kInf;
std::vector <LL> step, now;
//=============================================================
inline int read() {
  int f = 1, w = 0;
  char ch = getchar();
  for (; !isdigit(ch); ch = getchar())
    if (ch == '-') f = -1;
  for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
  return f * w;
}
void Chkmax(LL &fir, LL sec) {
  if (sec > fir) fir = sec;
}
void Dfs(int lth_) {
  if (lth_ == n) {
    printf("%d\n", now[0]);
    for (int i = 0; i < n - 1; ++ i) {
      printf("Merge:%lld %lld\n", step[i], step[i] + 1);
    }
    printf("\n");
    Chkmax(ans, now[0]);
    return ;
  }
  for (int i = 0; i < n - lth_; ++ i) {
    LL tmp1 = now[i], tmp2 = now[i + 1];
    step.push_back(i);
    now.erase(now.begin() + i);
    now.erase(now.begin() + i);
    now.insert(now.begin() + i, - tmp1 - tmp2);
    Dfs(lth_ + 1);
    step.pop_back();
    now.erase(now.begin() + i);
    now.insert(now.begin() + i, tmp2);
    now.insert(now.begin() + i, tmp1);
  }
}
//=============================================================
int main() { 
  n = read();
  for (int i = 1; i <= n; ++ i) {
    a[i] = read();
    now.push_back(1ll * a[i]);
  }
  Dfs(1);
  printf("%lld\n", ans);
  return 0;
}
/*
5
-1 1 1 1 -1
*/

\(n=1\) 时，合法的方案有：+。
\(n=2\) 时，有：--。
\(n=3\) 时，有：+--，--+。
\(n=4\) 时，有：++++，+---，-+--，--+-，---+。
\(n=5\) 时，有：-----，+++--，++--+，+--++，--+++，++-+-，+-++-，-+++-，-++-+，-+-++。
\(n=6\) 时，有：+++++-，++----，...
\(n=7\) 时，有：+++++++，++++---，+------，...
\(n=8\) 时，有：++++++--，+++-----，--------，...

对上面的分配方式有疑问，可以调整爆搜中的输入数据，从而得到获得合并方式。
发现 ~~没啥规律~~ 似乎 \(+/-\) 的数量有一定的规律。

当 \(+/-\) 的数量满足某种关系时就可以随意排列。
当 \(n\bmod 3=0\) 时，\(-\) 最多有 \(n-2\) 个。
当 \(n\bmod 3=1\) 时，\(-\) 最多有 \(n-1\) 个。
当 \(n\bmod 3=2\) 时，\(-\) 最多有 \(n\) 个。
\(+\) 每次减少 3 个，\(-\) 对应地增加 3 个，仍满足对应数量关系。

于是考虑 \(-\) 的数量与 \(n\) 的的关系。设有 \(m\) 个 \(-\)，发现满足下式：

\[\begin{aligned} n + \max(m) &= \begin{cases} 2n-2 &(n\bmod 3 = 0)\\ 2n-1 &(n\bmod 3 = 1)\\ 2n &(n\bmod 3 = 2)\\ \end{cases}\\ m'&= m - 3k\ (3k \le m) \end{aligned}\]

然后可以发现：

\[n+m \equiv 1 \pmod 3 \]

推广证明也很简单，考虑归纳。

首先可以发现 \(n\le 3\) 是满足上述结论的。

对于 \(n\ge 3\) 情况，假设 \(n'\le n\) 都满足上述结论。
考虑合并的最后一步，一定是由两个合法状态合并而来的。设这两个合法状态的长度分别为 \(n_1,n_2(1\le n_1,n_2< n)\)，\(-\) 的个数分别为 \(m_1,m_2\)。
显然对于合并后新状态，有：

\[\begin{aligned} n+m &= n + (n_1-m_1) + (n_2-m_2)\\ &= 2 n_1 + 2 n_2 - m_1 - m_2\\ &= 2 n_1 + 2 n_2 - ((n_1 + m_1) - n_1) - ((n_2+m_2)-n_2)\\ &= 2 n_1 + 2 n_2 - (1 - n_1) - (1 - n_2)\\ &= 3n_1+3n_2-2 \end{aligned}\]

则 \(n+m \equiv 3n_1+3n_2+1 \equiv 1\pmod 3\)，得证。

综上，某长度为 \(n\) 且含有 \(m\) 个 \(-\) 的分配方案合法的充要条件是：

至少有两个相邻位置的符号相等。
\(n+m\equiv 1\pmod 3\)。

考虑 DP 计算所有合法分配情况中的最优解。
考虑到影响合法的因素，设状态 \(f_{i,j,0/1,0/1}\) 表示：分配了前 \(i\) 位，前 \(i\) 位满足 \(n+m\bmod 3 = j\)，第 \(i\) 位为 \(0/1\)，是否有两个相邻位置符号相等。
初始化 \(f_{1,1,0,0} = -a_1\)，\(f_{1,2,1,0} = a_1\)，分别代表第一个位置为 \(-/+\)。其他 \(f = -\infin\)。
枚举上一个状态 \(f_{i-1,j,k,l}\) 大力转移，有：

\[\begin{aligned} f_{i,\ (j+1)\bmod 3,\ 0,\ l\lor [k=0]} &= \max(f_{i,j,k,l}) - a_i\\ f_{i,\ (j+2)\bmod 3,\ 1,\ l\lor [k=1]} &= \max(f_{i,j,k,l}) + a_i \end{aligned}\]

答案即为 \(\max(f_{n,1,0,1}, f_{n,1,1,1})\)。
时间复杂度 \(O(n)\)。

//知识点：找规律，DP
/*
By:Luckyblock
*/
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#define LL long long
const int kN = 2e5 + 10;
//=============================================================
int n, a[kN];
LL f[kN][3][2][2]; //前 i 个数，i + "-"的个数 = j，这一位为 0/1，是否有连续的符号。
//=============================================================
inline int read() {
  int f = 1, w = 0;
  char ch = getchar();
  for (; !isdigit(ch); ch = getchar())
    if (ch == '-') f = -1;
  for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
  return f * w;
}
void Chkmax(LL &fir, LL sec) {
  if (sec > fir) fir = sec;
}
void Chkmin(int &fir, int sec) {
  if (sec < fir) fir = sec;
}
//=============================================================
int main() { 
  n = read();
  for (int i = 1; i <= n; ++ i) a[i] = read();
  if (n == 1) {
    printf("%d\n", a[1]);
    return 0;
  }
  memset(f, 128, sizeof (f));
  f[1][1][1][0] = a[1];
  f[1][1 + 1][0][0] = -a[1];
  for (int i = 2; i <= n; ++ i) {
    for (int j = 0; j <= 2; ++ j) {
      for (int k = 0; k <= 1; ++ k) {
        for (int l = 0; l <= 1; ++ l) {
          Chkmax(f[i][(j + 1) % 3][1][l | (k == 1)], f[i - 1][j][k][l] + a[i]);
          Chkmax(f[i][(j + 1 + 1) % 3][0][l | (k == 0)], f[i - 1][j][k][l] - a[i]);
        }
      }
    }
  }
  printf("%lld\n", std::max(f[n][1][0][1], f[n][1][1][1]));
  return 0;
}
/*
5
1 -1 1 -1 1
*/

总结

位运算各位相互独立，可以分开考虑。
数据范围比较神必的时候观察特殊性质。
爆搜枚举所有方案，找规律。

posted @ 2020-11-17 14:38 Luckyblock 阅读(91) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

Luckyblock

身与华落，心将香飞

Codeforces Round #676

写在前面

A

B

C

D

E

总结

公告