P2487 [SDOI2011]拦截导弹

知识点: CDQ分治，优化 DP

原题面 Luogu

题意简述

给定一长度为 \(n\) 的序列，序列中元素 \(i\) 有两个属性 \(h_i,v_i\)。
选择一个子序列 \(b\)，满足 \(h_{b_i} \le h_{b_j}, v_{b_i} \le v_{b_j}(j<i)\)。
求满足条件的子序列的最长长度。
若从所有满足条件且长度最长的子序列中随机选择一个，求所有元素能够出现在子序列中的概率。
\(1\le n\le 5\times 10^4\)，\(1\le h_i, v_i\le 10^9\)。

分析题意

二维 LIS 问题。

设 \(f1_i\) 为以元素 \(i\) 为结尾的 LIS 的长度，\(g1_i\) 表示这样的 LIS 的个数。
则有一个显然的暴力：

\[f1_i = 1 + \max_{j=1}^{i-1} f1_j[h_j\ge h_i][v_j\ge v_i] \]

\[g1_i = \sum_{j=1}^{i-1} g1_j [h_j\ge h_i][v_j\ge v_i][f1_j + 1 = f1_i] \]

第一问答案即为 \(\max\limits_{i=1}^{n} f1_i\)。

考虑第二问，设\(f2_i\) 为以元素 \(i\) 为开头的 LIS 的长度，\(g2_i\) 表示这样的 LIS 的个数。
将原序列翻转，再做一遍上面的 DP 即可更新 \(f2, g2\)。
若元素 \(i\) 出现在整个序列的 LIS 中，则必有：

\[f1_i + f2_{n-i+1} - 1 = \max_{i=1}^{n} f1_i \]

表示 LIS 可以通过包含 \(i\) 的两端拼接而成。
此时元素 \(i\) 能够出现在子序列中的概率即为 \(\dfrac{g1_i\times g2_i}{\sum\limits_{i=1}^{n}{g1_i}}\)。
否则概率为 \(0\)。

复杂度 \(O(n^2)\)，期望得分 \(30\text{pts}\)。

总共有 \(O(n^2)\) 对转移，跑不过，考虑优化。
观察上述转移方程，能够用来更新 \(f_i\) 的 \(f_j\) 必须满足 \(j<i, h_j\ge h_i, v_j\ge v_i\)。
是一个三维偏序的形式，考虑 Cdq 分治。

考虑 \(O(n^2)\) 对转移，将其看作 \(O(n^2)\) 个点对。
设当前处理的区间为 \([l, r]\)，考虑Cdq 分治的一般过程：

若 \(l = r\)，返回。
设区间中点为 \(mid\)，递归处理 \([l,mid]\) 和 \([mid + 1, r]\)。
计算横跨 \(mid\) 的转移的贡献。

计算贡献时，套路地维护双指针，并用线段树维护 \(f\) 的前缀最大值和 \(g\) 的前缀和。

但是这样有问题。
通过 Cdq 改变了转移顺序，不能保证递归 \([mid + 1, r]\) 时所有的 \(f_i(i<mid + 1)\) 都被更新过。
考虑改变分治的过程：

若 \(l = r\)，返回。
设区间中点为 \(mid\)，递归处理 \([l,mid]\)。
计算横跨 \(mid\) 的转移的贡献。
递归处理 \([mid + 1, r]\)。

正确性？
观察 Cdq 的递归树。
114
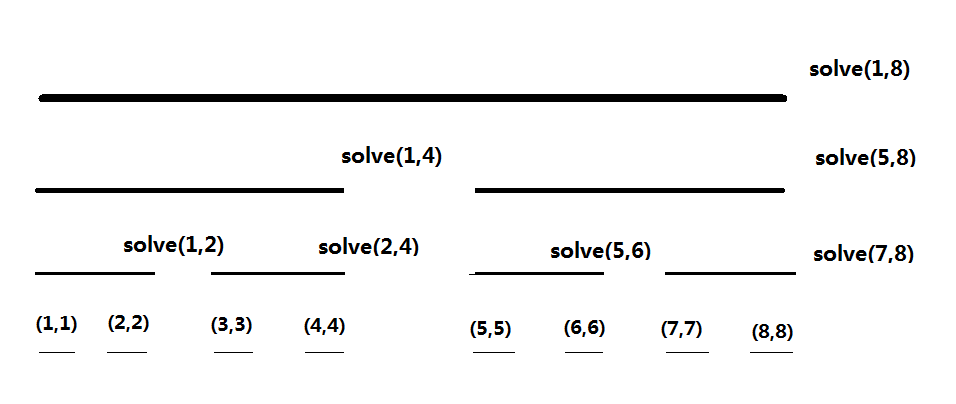
在更新 \([mid + 1, r]\) 之前，\([l, mid]\) 的 DP 值均已更新完毕。
考虑横跨 \(mid\) 的转移，发现则 \(mid + 1\) 的 DP 值一定会被更新到。

考虑 \([mid + 1, r]\) 的递归过程，会先递归到 \([mid + 1, mid + 2]\)。
在计算横跨 \(mid + 1\) 的转移时，\(mid + 2\) 的 DP 值也会被更新。
返回上一层 \([mid + 1, mid + 4]\)，\([mid + 1, mid + 2]\) 的 DP 值均已更新完毕。
又回到了一开始的形式，以此类推即可。

一点小 Trick

关于 Cdq 改变处理顺序的一点小 Trick。

三维偏序中的 Cdq 是这样的：

void Cdq(int l_, int r_) {
  if (l_ == r_) return ;
  Cdq(l_, mid), Cdq(mid + 1, r_);
  Solve(); //处理横跨 mid 的点对
}

本题的 Cdq 理论上应该是这样的：

void Cdq(int l_, int r_) {
  if (l_ == r_) return ;
  Cdq(l_, mid);
  Solve();
  Cdq(mid + 1, r_);
}

如果仅仅这样写的话，会 WA 穿掉。
原因是在 Solve 中，序列的顺序会发生变化。
可能会使 \([mid + 1, r]\) 不满足应有的单调性，接下来递归处理的时候会出错。
应该加个排序，写成这样：

void Cdq(int l_, int r_) {
  if (l_ == r_) return ;
  sort(l_, r_);
  Cdq(l_, mid);
  Solve();
  Cdq(mid + 1, r_);
}

一些细节

注意每次考虑横跨 \(mid\) 的转移时，都将线段树清空。

线段树维护的 \(f\) 中，可能有相等的 \(f\)。
如果它们为区间最大值，它们的出现次数应累加。

注意线段树中更新的顺序。

代码实现

//知识点：CDQ分治，优化 DP 
/*
By:Luckyblock
*/
#include <algorithm>
#include <cstdio>
#include <ctype.h>
#include <cstring>
#define ll long long
const int kMaxn = 5e4 + 10;
//=============================================================
struct Rocket {
  ll t, h, v;
} a[kMaxn];
ll n, maxh, maxv, maxf, f1[kMaxn], f2[kMaxn], data[kMaxn];
double sum, g1[kMaxn], g2[kMaxn];
//=============================================================
inline ll read() {
  ll f = 1, w = 0;
  char ch = getchar();
  for (; !isdigit(ch); ch = getchar())
    if (ch == '-') f = -1;
  for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
  return f * w;
}
void GetMax(ll &fir_, ll sec_) {
  if (sec_ > fir_) fir_ = sec_;
}
bool CompareRocket(Rocket fir, Rocket sec) {
  return fir.t < sec.t;
}
bool CompareCdq(Rocket fir, Rocket sec) {
  if (fir.h != sec.h) return fir.h > sec.h;
  return fir.t < sec.t;
}
struct SegmentTree {
  #define ls (now_<<1)
  #define rs (now_<<1|1)
  #define mid ((L_+R_)>>1)
  ll maxval[kMaxn << 2];
  double cnt[kMaxn << 2];
  void Build(int now_, int L_, int R_) {
    if (! maxval[now_]) return ;
    maxval[now_] = 0;
    cnt[now_] = 0;
    if (L_ == R_) return ; //注意顺序 
    Build(ls, L_, mid), Build(rs, mid + 1, R_);
  }
  void Pushup(int now_) { //注意 maxval[ls] = maxval[rs]。 
    cnt[now_] = (maxval[ls] >= maxval[rs]) * cnt[ls];
    cnt[now_] += (maxval[ls] <= maxval[rs]) * cnt[rs];
    maxval[now_] = std :: max(maxval[ls], maxval[rs]);
  }
  void Modify(int now_, int L_, int R_, int pos_, ll val_, double cnt_) {
    if (L_ == R_) {
      if (maxval[now_] < val_) {
        maxval[now_] = val_;
        cnt[now_] = cnt_;
      } else if (maxval[now_] == val_) {
        cnt[now_] += cnt_;
      }
      return ;
    }
    if (pos_ <= mid) Modify(ls, L_, mid, pos_, val_, cnt_);
    else Modify(rs, mid + 1, R_, pos_, val_, cnt_);
    Pushup(now_);
  }
  ll Query(int now_, int L_, int R_, int ql_, int qr_, double &cnt_) {
    if (ql_ <= L_ && R_ <= qr_) {
      cnt_ = cnt[now_];
      return maxval[now_];
    }
    double cntl = 0, cntr = 0;
    ll maxvall = 0, maxvalr = 0;
    if (ql_ <= mid) maxvall = Query(ls, L_, mid, ql_, qr_, cntl);
    if (qr_ > mid) maxvalr = Query(rs, mid + 1, R_, ql_, qr_, cntr);
    cnt_ = (maxvall >= maxvalr) * cntl + (maxvall <= maxvalr) * cntr;
    return std :: max(maxvall, maxvalr);
  }
  #undef mid
} t;
void Prepare() {
  n = read();
  for (int i = 1; i <= n; ++ i) {
    a[i] = (Rocket) {i, read(), read()};
    data[i] = a[i].v;
    GetMax(maxh, a[i].h);
  }
  std :: sort(data + 1, data + n + 1);
  for (int i = 1; i <= n; ++ i) {
    if (data[i] != data[i - 1]) {
      data[++ maxv] = data[i];
    }
  }
  for (int i = 1; i <= n; ++ i) {
    a[i].v = std :: lower_bound(data + 1, data + maxv + 1, a[i].v) - data;
  }
  for (int i = 1; i <= n; ++ i) {
    f1[i] = f2[i] = 1;
    g1[i] = g2[i] = 1.0;
  }
}
#define mid ((l_+r_)>>1)
void Cdq1(int l_, int r_) {
  if (l_ == r_) return ;
  std :: sort(a + l_, a + r_ + 1, CompareRocket);
  Cdq1(l_, mid);
  std :: sort(a + l_, a + mid + 1, CompareCdq);
  std :: sort(a + mid + 1, a + r_ + 1, CompareCdq);
  t.Build(1, 1, n);
  for (int p1 = l_, p2 = mid + 1; p2 <= r_; ++ p2) {
    for (; p1 <= mid && a[p1].h >= a[p2].h; ++ p1) {
      t.Modify(1, 1, n, a[p1].v, f1[a[p1].t], g1[a[p1].t]);
    }
    double cnt = 0;
    ll f = t.Query(1, 1, n, a[p2].v, n, cnt); //v 写成 h
    if (f1[a[p2].t] < f + 1) {
      f1[a[p2].t] = f + 1;
      g1[a[p2].t] = cnt;
    } else if (f1[a[p2].t] == f + 1) {
      g1[a[p2].t] += cnt; 
    }
  }
  Cdq1(mid + 1, r_);
}
void Cdq2(int l_, int r_) {
  if (l_ == r_) return ;
  std :: sort(a + l_, a + r_ + 1, CompareRocket);
  Cdq2(l_, mid);
  std :: sort(a + l_, a + mid + 1, CompareCdq);
  std :: sort(a + mid + 1, a + r_ + 1, CompareCdq);
  t.Build(1, 1, n);
  for (int p1 = l_, p2 = mid + 1; p2 <= r_; ++ p2) {
    for (; p1 <= mid && a[p1].h >= a[p2].h; ++ p1) {
      t.Modify(1, 1, n, a[p1].v, f2[a[p1].t], g2[a[p1].t]); 
    }
    double cnt = 0;
    ll f = t.Query(1, 1, n, a[p2].v, n, cnt);
    if (f2[a[p2].t] < f + 1) {
      f2[a[p2].t] = f + 1;
      g2[a[p2].t] = cnt;
    } else if (f2[a[p2].t] == f + 1) {
      g2[a[p2].t] += cnt;
    }
  }
  Cdq2(mid + 1, r_);
}
//=============================================================
int main() {
  Prepare();
  Cdq1(1, n);
  for (int i = 1; i <= n; ++ i) GetMax(maxf, f1[i]);
  for (int i = 1; i <= n; ++ i) sum += (f1[i] == maxf) * g1[i];
  for (int i = 1; i <= n; ++ i) {
    a[i].t = n - a[i].t + 1;
    a[i].h = maxh - a[i].h + 1;
    a[i].v = maxv - a[i].v + 1;
  }
  std :: sort(a + 1, a + n + 1, CompareRocket);
  
  Cdq2(1, n);
  printf("%lld\n", maxf);
  for (int i = 1; i <= n; ++ i) {
    if (f1[i] + f2[n - i + 1] - 1 != maxf) printf("%.5lf ", 0.0);
    else printf("%.5lf ", g1[i] * g2[n - i + 1] / sum);
  }
  return 0;
}

posted @ 2020-08-30 22:20 Luckyblock 阅读(188) 评论(0) 编辑收藏举报

刷新页面返回顶部

Luckyblock

身与华落，心将香飞