「笔记」容斥原理

目录

• 容斥原理
  • 证明
  • 交集
• min-max 容斥
  • 证明
• 写在最后

---

容斥原理

用于计算多个集合并集的大小。

\[\small\text{一张用烂的图} \]

\[\small\text{from Wikipedia} \]

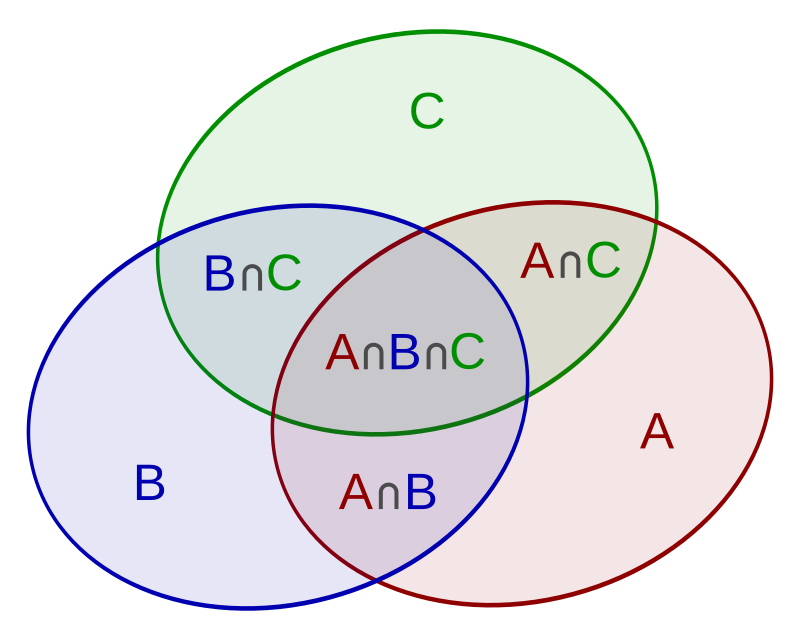
先将所有 单个集合 的大小计算出来，减去所有 两个集合 相交的部分，加回所有 三个集合 相交的部分，减去所有 四个集合 相交的部分，依此类推，一直计算到 所有集合 相交的部分。

写成数学公式形式：

\[{\displaystyle {\begin{aligned}\left|\bigcup _{i=1}^{n}A_{i}\right|={}&\sum _{i=1}^{n}|A_{i}|-\sum _{1\leq i<j\leq n}|A_{i}\cap A_{j}|+\sum _{1\leq i<j<k\leq n}|A_{i}\cap A_{j}\cap A_{k}|-\cdots +(-1)^{n-1}\left|A_{1}\cap \cdots \cap A_{n}\right|.\end{aligned}}} \]

即为：

\[{\displaystyle \left|\bigcup _{i=1}^{n}A_{i}\right|=\sum _{k=1}^{n}(-1)^{k+1}\left(\sum _{1\leq i_{1}<\cdots <i_{k}\le n}|A_{i_{1}}\cap \cdots \cap A_{i_{k}}|\right)} \]

证明

需证明通过上述方法计算，每个元素仅被覆盖了一次。
考虑一个出现在 \(m\) 个集合中的元素 \(x\)。

按照上述方法：

1. 选取一个集合时，显然 \(x\) 在其中出现次数为 \({m\choose 1}\)。
2. 选取两个集合时，两集合贡献为其并集的大小。
   则 \(x\) 在两集合中均出现时 才有贡献。
   出现次数为 满足条件的方案数，即 \({m\choose 2}\)。
   贡献为其相反数 \(-{m\choose 2}\)。
3. 选取三个集合时，分析过程同上，出现次数为 \({m\choose 3}\)。
4. 以此类推，选取集合数 \(>m\) 时，\(x\) 不会在并集中出现，贡献为 \(0\)。

则 \(x\) 的出现次数为：

\[\begin{aligned} Cnt =& {m\choose 1} - {m\choose 2} +... + (-1)^{m-1}{m\choose m}\\ =& \sum_{i=1}^{m}(-1)^{i-1}{m\choose i} \end{aligned}\]

发现这玩意挺优美，考虑二项式定理：

\[\begin{aligned} Cnt =& \sum_{i=1}^{m}(-1)^{i-1}{m\choose i}\\ = & -\sum_{i=1}^{m}(-1)^{i}{m\choose i}\\ = &{m\choose 0} -{m\choose 0} -\sum_{i=1}^{m}(-1)^{i}{m\choose i}\\ = &{m\choose 0} -\sum_{i=0}^{m}{m\choose i}(-1)^{i}\\ = &1-(-1+1)^m\\ = &1 \end{aligned}\]

得证。

交集

用全集减去 补集的并集 求得，即 补集的并集 的补集。

\[\bigcap _{{i=1}}^{n}A_{i} = |U|-\left|\bigcup_{i=1}^n\overline{A_i}\right| = \overline {\bigcup _{{i=1}}^{n}\overline {A}_{i}} \]

正确性显然，略证：
\(\overline{A_i}\) 为除 \(A_i\) 外的元素，\(\overline{A_i} \cup \overline{A_j}\) 为除 \(A_i\cap A_j\) 外的元素。
\(\left|\bigcup\limits_{i=1}^n\overline{A_i}\right|\) 则为除 \(\bigcap\limits_{{i=1}}^{n}A_{i}\) 外的元素。
其补集即为交集。

---

min-max 容斥

设 \(S\) 是一个可重数集，\(\min\{S\},\max\{S\}\) 分别表示数集中的 最小/最大 值。
则有下式成立：

\[\begin{aligned} \max \{S\} &= \sum_{T\subseteq S}(-1)^{|T|-1} \min \{T\}\\ \min \{S\} &= \sum_{T\subseteq S}(-1)^{|T|-1} \max \{T\} \end{aligned}\]

证明

以式子 1 为例：

显然，仅当 \(T = \{\{\max\{S\}\}\) 时，\(\min\{T\} = \max\{S\}\)。
（可能有多个相同的最大值，随意钦定一个即可）

对于其他子集 \(T\not= \{\{\max\{S\}\}\)，考虑钦定一个数为 \(\min \{T\}\)。

设 \(\min \{T\}\) 为 \(x\)，则 \(T\) 中的其他数均 \(\ge x\)。
设 \(\left|\{y\mid y\in S, y\ge x\}\right| = k\)，则 \(\min \{T\}=x\) 有 \(2^{\left|S\right|-k}\) 种方案。
显然，在这 \(2^{\left|S\right|-k}\) 个子集中，\(\left|T\right|\) 为 奇/偶 数的方案各有 \(2^{\left|S\right|-k-1}\) 种，它们正负抵消，总贡献为 \(0\)。

此时仅有 \(T = \{\{\max\{S\}\}\) 时，会对答案作出 \(\max\{S\}\) 的贡献。
结论成立。

式子 2 同理可证。

---

写在最后

水炊老师太神了吧 /fad
单马尾文文好可爱（