P4158 [SCOI2009]粉刷匠

知识点: DP

原题面

？这波算是大暴力草了过去

---

题意简述

给定一 \(N\times M\) 的空白矩阵，以及每个格子的目标颜色（为只能为红 / 蓝）。
每次可选择一行上连续的一段，涂上一种颜色。
每个格子最多只能被粉刷一次。
可涂色 \(T\) 次，求最多正确粉刷的个数。
\(1\le N,M\le 500,0\le T\le 2500\)。

---

分析题意

注意 每个格子最多只能被粉刷一次。
由于这个性质，一个格子不会被多次更改颜色。
无后效性，可考虑线性 DP。

一开始没注意到，往区间 DP 往上莽了一阵

---

先考虑一行的情况：

把红色格子当作 0，蓝色看成 1。
显然一段连续同色区段，可以一次涂完。
考虑将连续同色区段合并，如下图形式：

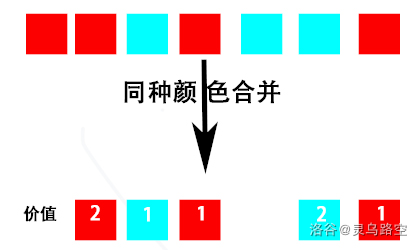
发现合并后的一行变成 0/1 交替的形式。
上一个格子与这一个目标状态一定不同。
以下提到格子，均指合并后的格子。

---

考虑新加入一个格子 \(i\)，对花费的影响。
由上，影响新格子的，只有最后一个格子的状态。

1. 当上一个格子刷错时，可顺便刷对新格子，花费不变。
2. 当上一个格子刷对时，要想刷对新格子，必须多花费一次。
3. 当上一个格子刷对时，刷错新格子，总花费不变。
4. 当上一个格子刷错时，刷错新格子，必须多花费一次。

格子刷错对答案无贡献，刷对时对答案贡献为 \(val_i\)

设 \(f_{i,j,k, 0/1}\) 表示，第 \(i\) 行，在 \(1\sim j\) 中刷 \(k\) 次，第 \(j\) 个格子刷 错/对时，能刷对的最多格子数。
设 \(val_{i,j}\) 为格子 \((i,j)\) 的权值，显然有：

\[\begin{aligned} &f_{i,j,0} = \max\{f_{i,j-1,k,1},\ f_{i,j-1,k-1,0}\}\\ &f_{i,j,1} = \max\{f_{i,j-1,k,0},\ f_{i,j-1,k-1,1}\}+val_{i,j} \end{aligned}\]

合并后每行格子长度变小，复杂度上限 \(O(nmT)\)。

---

显然，第 \(i\) 行刷 \(j\) 次后，能刷对的最多格子数为：

\[val_{i,j} = \max\{f_{i,n,k,0}, f_{i,n,k,1}\} \]

每行只能做一次贡献，涂色总次数为 \(T\)，自此变成了一个分组背包问题。

数据范围较小，可暴力 \(O(nT^2)\) 实现。
直接暴力显然显然过不去，加个小剪枝，使每行涂色数 \(\le\) 格子数即可。

---

代码实现

数组 \(val\) 有两种含义，注意重新赋值时含义的变化。

//知识点:DP
/*
By:Luckyblock
*/
#include <cstdio>
#include <ctype.h>
#include <algorithm>
#define ll long long
const int kMaxn = 55;
const int kMaxT = 2510;
//=============================================================
int n, m, T, ans, lth[kMaxn], val[kMaxn][kMaxT]; //val:第i行第j个价值 ->第i行选j个贡献 
char s[kMaxT];
int f[kMaxn][kMaxn][kMaxT][2]; //0×,1√ 
int g[kMaxn][kMaxT];
//=============================================================
inline int read() {
  int f = 1, w = 0; char ch = getchar();
  for (; !isdigit(ch); ch = getchar()) if (ch == '-') f = -1;
  for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
  return f * w;
}
//=============================================================
int main() {
  n = read(), m = read(), T = read();
  for (int i = 1; i <= n; ++ i) {
    scanf("%s", s + 1);
    for (int j = 1; j <= m; ++ j) {
      int x = s[j] - '0';
      if (s[j] != s[j - 1]) lth[i] ++; //格子数增加 
      val[i][lth[i]] ++; //合并 
    }
  }
  
  //分别考虑每行，求第i行，在 1~j 中刷 k 次，第 j 个格子刷 错/对时，能刷对的最多格子数。  
  for (int i = 1; i <= n; ++ i) {
    for (int j = 1; j <= lth[i]; ++ j) {
      for (int k = 1; k <= T; ++ k) {
        f[i][j][k][0] = std :: max(f[i][j - 1][k][1], f[i][j - 1][k - 1][0]);
        f[i][j][k][1] = std :: max(f[i][j - 1][k][0], f[i][j - 1][k - 1][1]) + val[i][j];
      }
    }
  }
  
  //求第 i 行刷 j 次后，能刷对的最多格子数为 
  for (int i = 1; i <= n; ++ i) {
    for (int j = 0; j <= T; ++ j) {
      val[i][j] = std :: max(f[i][lth[i]][j][0], f[i][lth[i]][j][1]);
    }
  }
  
  //分组背包 
  for (int i = 1; i <= n; ++ i) {
    for (int j = 0; j <= T; ++ j) {
      for (int k = 0; k <= std :: min(lth[i], T); ++ k) { //小剪枝 
        if (j + k > T) break ;
        g[i][j + k] = std :: max(g[i][j + k], g[i - 1][j] + val[i][k]);
      }
    }
  }
  for (int i = 1; i <= T; ++ i) ans = std :: max(ans, g[n][i]);
  printf("%d\n", ans); 
  return 0;
}