P2501 [HAOI2006]数字序列

知识点: DP

原题面

太妙了，学到虚脱。

---

题意简述

给定一长度为 \(n\) 的数列 \(a\)，可将 \(a_i\) 改为任意整数 \(k\)，代价为 \(\mid a_i -k\mid\)。
求使数列变为单调严格上升序列，最少需要改变的个数。
及改变数最少时，最小的代价和。
\(1\le n\le 3.5\times 10^4, 1\le a_i\le 10^5\)。

---

分析题意

先搞掉第一问。

需要改变最少，则需保留得尽可能多。
考虑保留两个数的条件，对于 \(a_i,a_j(i < j)\)，若可保留，说明 \(a_i < a_j\) 且改变 \([i+1,j-1]\) 内的数，可使序列 \([i,j]\) 严格上升。

如数列 \(1, 4, 5, 3\) (无歧义)，虽然满足 \(1<3\)，但它们中间的两个数无论改成多少，都无法满足单增性质。

显然保留 \(a_i,a_j\) 的条件为：\(a_j-a_i \ge j-i\)。
移项，得 \(a_j - j \ge a_i - i\)。
发现保留 \(a_i\) 的条件为 \(a_i-i\) 单调不降。

设 \(b_i = a_i - i\)。
使用经典 \(O(n\log n)\) 的方法，求数列 \(b\) 的最长不下降子序列长度，即为答案。

---

来搞第二问。

发现使 \(a_i\) 单调上升的代价，等价于使 \(b_i\) 单调不降的代价。
有个结论：
对于区间 \([l,r]\)，使其单调不降，则存在分界点 \(k\)，使 \(b_i = b_l(i\le k), b_j = b_r (j>k)\)，此时代价最小。

如何证明这个听起来很扯皮的结论？

考虑做第一问时，顺便维护一下每个数的从哪里转移而来。
设转移前驱为 \(pre_i\)。
显然，\(pre_i\) 为满足 \(b_i \ge b_{pre_i}\) 的，且使子序列最长的位置。
则不存在 \(pre_i<j<i\)，使 \(b_j\le b_i\)，否则 \(pre_i = j\) 显然更优。

考虑 \(pre_i\) 和 \(b_i\) 之间的数 \(b_j\)，一定满足 \(b_j < b_{pre_i}\) 或 \(b_j>b_i\)，它们一定要被修改。
设 \(b_j\) 修改后为 \(c_j\)，显然 \(c_j\) 单调不降，且 \(b_{pre_i} \le c_j\le b_i\)。
则有下图形式：

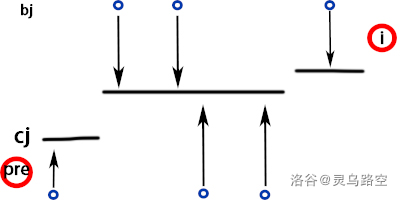
上图给出了一种修改的方案，考虑能否调整方案，使答案更优。
分类讨论：
对于一段被改为 \(c\) 的连续区间 \([l,r]\)：

1. 若 \(b_j < b_{pre_i}\) 的数量大于 \(b_j > b_{pre_i}\) 的数量，则 \(c\) 越小，代价越小。
   又要保证单调不降，则 \(c = c_{l-1}\) 时最优。
2. 若 数量相反，分析过程同上，\(c = c_{r+1}\) 时最优。
3. 若 数量相等，\(c\) 可取任意值。

则可对此方案进行调整：



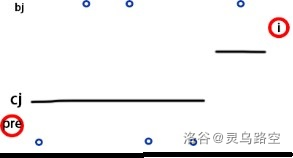
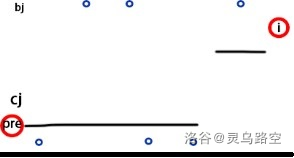
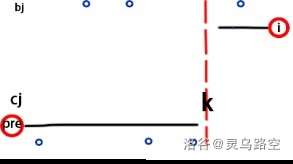
发现满足结论形式。

则对于任意不满足结论的方案，均可进行调整，使代价更小，最终必定调整至结论中的形式。

---

令 \(g_i\) 表示，最后一位是 \(b_i\) 时单调不降的代价。
枚举满足条件的前驱 \(pre\)，转移 \(b_i\)，
枚举的前缀满足：

• \(pre_i < i, b_{pre}\le b_i\)。
• 以\(b_{pre}\)结尾的 最长不降子序列长度 = 以 \(b_i\) 结尾的 - 1。

之后枚举分界 \(k\)，求得最小的代价。
有：

\[g_i = \min\{g_{pre} + \sum_{j=pre+1}^{k}\mid b_j-b_{pre}\mid + \sum_{j=k+1}^{i-1}\mid b_j-b_{i}\mid\} \]

后面那一大堆 \(\sum\) 可以用前缀后缀和优化。
复杂度 \(O(n^2)\) 级别？但数据随机，\([pre_i,i]\) 的长度较小，可以跑过去。

---

代码实现

代码中用 vector 记录长度为 \(i\) 的最长不降子序列的结尾，再通过判断确定转移前缀。
\(from\) 表示转移前缀，\(pre\) 表示前缀和。
注意不开 long long 爆零两行泪。

//知识点:DP
/*
By:Luckyblock
*/
#include <vector>
#include <cstdio>
#include <ctype.h>
#include <cstring>
#include <algorithm>
#define ll long long
const int kMaxn = 3e4 + 5e3;
const int kInf = 1e9 + 2077;
//=============================================================
int n, lth, b[kMaxn];
int minn[kMaxn], f[kMaxn];
ll g[kMaxn], pre[kMaxn], suf[kMaxn];
//minn[i]: 长度为i 的最长不下降的最小结尾
//f[i]: 以i结尾最长不下降长度
//g[i] 最后一位是 b_i 时单调不降的代价
std :: vector <int> end[kMaxn]; //记录长度为 i 的最长不降子序列的结尾。   
//=============================================================
inline int read() {
  int f = 1, w = 0; char ch = getchar();
  for (; !isdigit(ch); ch = getchar()) if (ch == '-') f = -1;
  for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
  return f * w;
}
//=============================================================
int main() {
  n = read();
  for (int i = 1; i <= n; ++ i) b[i] = read() - i; 
  b[0] = - kInf, b[n + 1] = kInf; //边界 
  
  for (int i = 1; i <= n + 1; ++ i) { //到n + 1 
    int l = 0, r = lth;
    while (l < r) {
      int mid = (l + r + 1) >> 1;
      if (minn[mid] <= b[i]) l = mid;
      else r = mid - 1;
    }
    if (l == lth) ++ lth;
    f[i] = l + 1;
    minn[l + 1] = b[i];
    end[f[i]].push_back(i); //记录长度为 f_i 的最长不降子序列的结尾
  } 
  
  end[0].push_back(0);
  memset(g, 20, sizeof(g));
  g[0] = 0;
  for (int i = 1; i <= n + 1; ++ i) {
    for (int j = 0, size = end[f[i] - 1].size(); j < size; ++ j) {
      int from = end[f[i] - 1][j];
      if (from > i || b[from] > b[i]) continue ; //合法性判断 
      pre[from] = suf[i - 1] = 0; //注意边界 
      for (int k = from + 1; k <= i - 1; ++ k) {
        pre[k] = pre[k - 1] + abs(b[k] - b[from]);
      }
      for (int k = i - 2; k >= from; -- k) {
        suf[k] = suf[k + 1] + abs(b[k + 1] - b[i]);
      }
      for (int k = from; k <= i - 1; ++ k) { //g[from]转移 
        g[i] = std :: min(g[i], g[from] + pre[k] + suf[k]); 
      }
    }
  }
  printf("%d\n%lld\n", n - lth + 1, g[n + 1]);
  return 0;
}