「笔记」DP从入土到入门

目录

• 习题
  • P5017 摆渡车
  • P4910 【帕秋莉的手环】
  • P4933 大师
  • P1439 【模板】最长公共子序列
  • P5858 「SWTR-03」Golden Sword
  • P5664 Emiya 家今天的饭
  • P1973 [NOI2011]NOI 嘉年华
  • P1270 “访问”美术馆
  • P2577 [ZJOI2004]午餐
  • P2501 [HAOI2006]数字序列
  • P4158 [SCOI2009]粉刷匠
  • P1295 [TJOI2011]书架
  • P1052 过河
  • P2051 [AHOI2009]中国象棋
  • CF79D Password
  • P1040 加分二叉树
  • P1273 有线电视网
  • P3287 [SCOI2014]方伯伯的玉米田
  • P2487 [SDOI2011]拦截导弹
  • P1846 游戏
  • P2495 [SDOI2011]消耗战
  • 拓扑序应用
  • P3478 [POI2008]STA-Station
  • CF708C Centroids
  • 「NOI2015」寿司晚宴
  • P6858 深海少女与胖头鱼
  • P3786 萃香抱西瓜
  • CF1437C Chef Monocarp
  • CF1437E Make It Increasing
  • CF1437F Emotional Fishermen
  • CF1433F Zero Remainder Sum
  • 「CSP-S 2020」函数调用
  • P3558 [POI2013]BAJ-Bytecomputer
  • CF1436D Bandit in a City
  • CF1422E Minlexes
  • CF1457C Bouncing Ball
  • P2943 [USACO09MAR]Cleaning Up G
  • 「SCOI2009」Windy 数
  • P4081 [USACO17DEC]Standing Out from the Herd P
  • 「HAOI2016」找相同字符
  • 「AHOI2009」同类分布
  • 「AHOI2013」 差异
  • 「JSOI2007」文本生成器
  • 「SDOI2014」数数
  • 「BJOI2019」奥术神杖
  • 「HEOI2014」大工程
  • P2900 [USACO08MAR]Land Acquisition G
  • 「SDOI2016」征途
  • CF311B Cats Transport
  • P2365 任务安排
  • 「SDOI2012」任务安排 3
  • 「APIO2018」铁人两项
  • P4719 【模板】"动态 DP"&动态树分治
  • P3403 跳楼机
  • CF1792E
  • 「NOIP2012」开车旅行
  • P4766 [CERC2014]Outer space invaders
• 学到了什么
  • 枚举边界
  • 无用决策
  • 预处理
  • 相对大小
  • 决策单调性
  • 可枚举性
  • 排序问题
  • 补集转化
  • 贡献合并
  • 区间查询
  • 差分
  • 倒序枚举
  • 数据结构直接维护
  • 确定元素是否位于方案中
  • 对于一类计数类树形 DP
  • 换根 DP
  • 分段 DP
  • AC 自动机上 DP
  • 斜率优化
  • 圆方树 DP
  • 动态 DP
  • 猜结论
  • 杂

去世选手请求重生。

习题

P5017 摆渡车

线性 DP

详见 P5017 摆渡车 - Luckyblock

算法一

设 $f_i$ 在 $i$ 时间发车，发车时等待的时间和的最小值。则显然有：

$$f_i = \min_{j\le i-m}(f_j + \sum_{j < t_k \le i}^{n}{(i-t_k)})$$

对于每个 $f_i$，当在 $i$ 时刻时发第一班车，$f_i$最大，则其初始值为：

$$f_i = \sum_{t_k<i}^{n} {(i-t_k)}$$

为保证载上所有人，最后一班车需在 $[t_{max}, t_{max}+m)$内发车，则：

$$ans = \min_{i=t_{max}}^{t_{max}+m}(f_i)$$

---

前缀和优化，设 ：

$$cnt_i=\sum\limits_{t_k\le i} 1,\ pos_i = \sum\limits_{t_k\le i}{t_k}$$

对于上式中的 $\sum\limits_{j < t_k \le i}{i-t_k}$，有：

$$\sum\limits_{j < t_k \le i}{i-t_k} = (cnt_i-cnt_j)\times i - (pos_i-pos_j)$$

替换状态转移方程即可。

---

优化转移方程，对于状态转移方程：

$$f_i = \min_{j\le i-m}(f_j + (cnt_i-cnt_j)\times i - (pos_i-pos_j))$$

显然，若 $j\le i-2m$，则在 $j+m$ 时刻可多发一班车，不影响在 $i$ 时刻发车，且答案不会变劣。
即：停车时间 $i- (j+m) < m$。

故转移方程可替换为：

$$f_i = \min_{i-2m\le j\le i-m}(f_j + (cnt_i-cnt_j)\times i - (pos_i-pos_j))$$

---

减去无用状态。

若 $cnt_i=cnt_{i-m}$，说明时间段 $[i-m,i]$内没有需要坐车的人。
则在 $i-m$ 时刻发车，在 $i$ 时刻不发车，不会使答案变劣，$f_i$ 是一个无用状态。

则可将状态转移方程改为：

$$f_i = \begin{cases}f_{i-m} &cnt_i=cnt_{i-m}\\ \min_{i-2m\le j\le i-m}(f_j + (cnt_i-cnt_j)\times i - (pos_i-pos_j))& \text{otherwise}\end{cases}$$

当满足 $t_i = t_{i-1}+m$ 时，有用的位置最多，为 $nm$ 个。

最后的复杂度 $O(nm^2 + t)$，期望得分 $100\text{pts}$。

---

算法二

由算法一，停车时间 $i- (j+m) < m$。
车往返一次时间 $m$，则人等车时间 $< 2m$。

设 $f_{i,j}$ 表示第 $i$ 个人，等待时间为 $j$，且前 $i$ 个人已到达的时间最小值。

初始值 $f_{1,i} = i$。

分类讨论：

1. 若 $t_{i+1} \le t_{i+1} + j$，则第 $i+1$ 个人可和 第 $i$ 个人坐同一辆车走。
   第 $i+1$ 个人的等待时间 $k = t_i+j-t_{i+1}$
   状态转移方程式为：

$$f_{i+1, k} = \min(f_{i+1, k},f_{i,j}+k )$$

2. 否则，枚举第 $i+1$ 个人的等待时间 $k$。
   $$k\in [\max(0, t_i + j + m - t_{i+1}), 2m)$$
   状态转移方程式同上，为：
   $$f_{i+1,k} = \min (f_{i+1}, k, f_{i,j} + k)$$

复杂度 $O(nm^2)$，期望得分 $100\text{pts}$。

代码 P5017 摆渡车 - Luckyblock

P4910 【帕秋莉的手环】

矩阵快速幂优化 DP 转移。

给定一个长度为 $n$ 的环，填入 金色或绿色。
不能有两个相邻的绿色。
多组数据, $T\le 10, n\le 10^{18}$

矩阵加速模板。

设 $f_{i,0/1}$ 为当前填到第 $i$ 位，第一个位置为 金色/绿色 的合法方案数。
分成第一个位置为 绿/金讨论：

1. 第一个位置为绿色时，$f_{1,0} = 0,f_{1,1} = 1$。
   由于不能有两个相邻的绿色，则结尾珠子必为金色。
   其对答案的贡献为 $f_{n,0}$
2. 第一个位置为金色时，$f_{1,0} = 1, f_{1,1} = 0$。
   此时结尾珠子颜色任意。
   其对答案的贡献为 $f_{n,0} + f_{n,1}$

状态转移方程：
$f_{i,0} = f_{i-1,0} + f_{i-1,1}$
$f_{i,1} = f_{i-1,0}$

复杂度 $O(Tn)$，期望得分 $\text{60pts}$。

上式显然可矩阵加速，转移矩阵如下：

$$\begin{bmatrix}f_{i-1,0}&f_{i-1,1}\end{bmatrix} \times \begin{bmatrix}1&1\\1&0\end{bmatrix} = \begin{bmatrix}f_{i,0}&f_{i,1}\end{bmatrix}$$

复杂度 $O(T\log n)$，期望得分 $\text{100pts}$。

代码 P4910 【帕秋莉的手环】 - Luckyblock

P4933 大师

线性 DP。

给定一长度为 $n$ 的序列 $h$。
求方向为从左到右的，等差数列个数。
$n\le 10^3, h_{max} \le 2 \times 10^4$

显然的线性DP。
设 $f_{i,j}$ 表示 最后一项是$h_i$，公差为 $j$ 的等差数列的个数。

转移到 $i$ 时，枚举前一个元素 $k$，公差 $j$ 即为 $h_i - h_k$。
最后一项是 $h_k$，公差为 $j$ 的等差数列的个数为 $f_{k,j}$。

如图，在其末尾添加一新元素，则显然有 $f_{i,j} = f_{k,j} +1$。
可能存在多个公差为 $j$ 的位置 $k$，则有状态转移方程式：

$$f_{i,h_i - h_k} = \sum_{k<i}{f_{k,h_i - h_k} +1}$$

需要枚举当前位置 和 前一个位置。
复杂度 $O(n^2)$，稳过。

公差为负数怎么办？

1. 为所有计算出的公差加上一个偏移量。
2. 正着反着做两次DP，并将两次的贡献求和。

一种空间换时间，一种时间换空间。
代码中使用了时间换空间的做法。

代码 P4933 大师 - Luckyblock

P1439 【模板】最长公共子序列

线性 DP。

给定 $1,2,\dots n$ 的两个排列 $a,b$，求其最长公共子序列。
$n\le 10^5$

算法一

有一个极其显然的做法。
设 $f_{i,j}$ 为，$a$ 中匹配到第$i$ 位，$b$ 中匹配到第 $j$ 位时，最长公共子序列的长度。

讨论 $a_i$ 与 $b_j$ 是否相等，则有：
$f_{i,j} = \begin{cases}f_{i-1,j-1} +1 & a_i=b_j\\\max ({f_{i,j-1}, f_{i-1,j}}) & \text{otherwise}\end{cases}$

复杂度 $O(n^2)$，期望得分 $50\text{pts}$。

---

算法二

上述算法已无法再优化，考虑奇技淫巧。

排列中不存在重复元素，考虑建立一一映射关系。
令 $pos_{a_i} = i$，使 $a_i \Rightarrow i, b_i \Rightarrow pos_{b_i}$。
即发生如下的转化：

$$\begin{aligned}a&:3\ 1\ 5\ 4\ 2\\b&:2\ 3\ 4\ 5\ 1\end{aligned} \Longrightarrow \begin{aligned}&a:1\ 2\ 3\ 4\ 5\\&b:5\ 1\ 4\ 3\ 2\end{aligned}$$

显然映射后的 LCS 的长度不会受影响。

由于 $a_i$ 单调递增，则 LCS 也单调递增。
换言之，$b$ 中所有单调递增子序列，均是一公共子序列。
问题转化为，求 $b$ 最长的单调递增子序列的长度。
即经典的 LIS 问题。

使用 $O(n\log n)$ 算法求解即可，期望得分 $\text{100pts}$。

代码 P1439 【模板】最长公共子序列 - Luckyblock

P5858 「SWTR-03」Golden Sword

单调队列优化 DP。

给定 $n$ 个物品，编号为 $a_1\sim a_n$。
现需要将其按顺序放到容量为 $w$ 的箱子里。
每放入一个物品前，可以从箱子中取出 $s$ 个物品。
定义 第 $i$ 个物品的价值为，将其放入箱子后，箱中物品数 $\times a_i$，求最大价值和。
$1\le s\le w\le n \le 5.5\times 10^3, 0\le \mid a\mid \le 10^9$

发现一些奇妙性质。

1. 已经放入箱子的物品本质相同，对之后放入物品的贡献都为 $1$。
2. 欲使加入新物品后，箱子内物品数为 $j$，可在物品数为 $j-1$ 直接加入，或删去 $\le s$ 个物品。
   但两种方法对答案的贡献等价。

则有非常显然的做法。

设 $f_{i,j}$ 表示，放到第 $i$ 个物品，箱子里有 $j$ 个元素的最大价值和。

$$f_{i,j} = \max_{k=j-1}^{\min\{j+s-1,w\}} \{ f_{i-1,k} \} + j\times a_i$$

转移时只与 $i-1$ 有关，则 $i$ 维可以滚动数组滚掉，保证空间复杂度。
需每次都将 $f_{now}$ 初始化为负无穷。

注意循环边界的细节。

复制复制
for (int i = 1; i <= n; ++ i, now ^= 1) {
  memset(f[now], 128, sizeof(f[now]));
  for (int j = 1; j <= min(i, w); ++ j) {
    for (int k = j - 1; k <= min(i, min(j + s - 1, w)); ++ k) {
      f[now][j] = max(f[now][j], f[now ^ 1][k] + (ll) j * a[i]);
    }
  }
}

时间复杂度上限 $O(n^3)$，在 $s=w=n$ 时复杂度最高。
在随机数据下能骗到 $\text{85pts}$。

---

被 $\text{Subtask 4}$ 卡掉了咋办啊？
观察代码：

for (int j = 1; j <= min(i, w); ++ j) 
  for (int k = j - 1; k <= min(i, min(j + s - 1, w)); ++ k) 

发现 $k$ 的范围区间，随 $j$ 的增加，单调右移，考虑单调队列优化。
优化掉一重循环，省去了枚举 $k$ 的复杂度。

复杂度 $O(n^2)$，期望得分 $\text{100pts}$

代码 P5858 「SWTR-03」Golden Sword - Luckyblock

P5664 Emiya 家今天的饭

线性 DP，容斥

赛场上硬刚64pts 2.5h，最后样例没过。
没时间写爆搜，交了一份自己也不知道在干什么的代码，获得了 8pts 的好成绩。
留下了极大的心理阴影。
消除恐惧的最好方法，就是直面恐惧。
加油，奥利给！

给定一 $n\times m$ 的矩阵 $a$。
从矩阵中取出一个集合，满足下列要求：

1. 非空。
2. 每一行只能选择一个元素。
3. 属于同一列的元素数 $\le \left\lfloor\frac{n}{2}\right\rfloor$。

一个集合的价值定义为所有元素的乘积。
求所有满足条件的 集合的权值 之和，答案对 $998244353$ 取模。
$1\le n\le 100, 1\le m \le 2000, 0\le a_{i,j} \le 998244353$。

考虑容斥，容易想到，合法集合权值和 = 总权值和 - 不合法集合权值和。

对于总权值和：
每一行可以选择 1 个元素，或者不选。
选择 1 个元素时，其对乘积的贡献为 $a_{i,j}$，不选时贡献为 1。
最后减去空集的情况（其贡献为 1），则总权值和为：

$$\prod_{i=1}^{n}\sum_{j=1}^{m}a_{i,j} - 1$$

对于不合法集合权值和：
由条件 3 可知，不合法集合中，只存在一个不合法列，使集合中位于该列的元素数 $> \left\lfloor\frac{k}{2}\right\rfloor$。

考虑通过枚举固定这一列。
判断某一集合是否合法，只需已知 位于该列的元素数，和位于其他列的元素数，求差值即可。

令枚举固定的一列为 $now$，则可设计状态：$f_{i,j,k}$ 表示：前 $i$ 行中，$now$ 列中 选择了 $j$ 个，其他列中选择了 $k$ 个的权值和。

令 $s_{i,now} = \sum\limits_{j=1}^{m}a_{i,j} - a_{i,now}$，表示一行中非 $now$ 行的元素之和。
则有显然的转移方程：

$$f_{i,j,k} = f_{i-1,j,k} + f_{i-1,j-1,k}\times a_{i,now} + f_{i-1,j,k-1} \times s_{i,now}$$

复杂度 $O(n^3m)$，期望得分 $84\text{pts}$。

---

考虑优化：
由上述算法，判断集合是否合法，仅需知道 被枚举列和 其他列元素数的差值。
分别记录两种元素的个数是没有必要的。

考虑直接记录差值。
算法四转移方程中 $f_{i-1,j-1,k}\rightarrow f_{i-1,j,k}$ 和 $f_{i-1,j,k-1}\rightarrow f_{i-1,j,k}$，可看做差值的 增大 / 减小。

同样令固定的一列为 $now$，可设计新状态，令 $f_{i,j}$ 表示，前 $i$ 行中， $now$ 列中 选择个数 与 其他列个数差值为 $j$ 时的权值和。

令 $s_{i,now} = \sum\limits_{j=1}^{m}a_{i,j} - a_{i,now}$，表示一行中非 $now$ 行的元素之和。
则有状态转移方程：

$$f_{i,j} = f_{i-1,j} + f_{i-1,j-1} \times a_{i,now}+ f_{i-1,j+1}\times s_{i,now}$$

复杂度 $O(n^2m)$，期望得分 $100\text{pts}$。

代码 P5664 Emiya 家今天的饭 - Luckyblock

P1973 [NOI2011]NOI 嘉年华

线性 DP。

参考: stO FlashHu 的题解 Orz

蒟蒻尽量把悟到的信息都放了上来。
比较啰嗦，望见谅。

给定 $n$ 个事件，第 $i$ 个事件从 $S_i$时刻开始，持续 $T_i$ 时刻。
可将它们分到两个地点中的一个，或者放弃。
同一地点事件可同时发生，两个事件不可同时发生在不同地点。
求

1. 无限制时，事件数较小的地点 的事件数。
2. 不放弃第 $i$ 个事件时，事件数较小的地点 的事件数。

$1\le n \le 200, 0\le S_i\le10^9,1\le T_i\le 10^9$。

先离散化，下文中出现的 “时间” 均指离散化后的值。
显然，离散化后时间的最大值 $\le 2n$。

把事件看做线段，地点看做集合。
从 $S_i$时刻开始，持续 $T_i$ 时刻的事件记为 $[s_i,t_i]$。

有一个很显然的结论：
对于一个分配方案，若存在某被丢弃的事件，可加入到集合中。
将其加入，答案不会变劣。

由上，若向某一集合中添加了一条线段 $[L,R]$，则所有包含于 $[L,R]$ 的线段，都一定会被添加到该集合中。

则可考虑将一个区间内的完整线段合并，
设 $cnt_{i,j}$ 表示区间 $[i,j]$ 内的完整线段数。
暴力 $O(n^3)$ 预处理即可。

---

先搞掉子任务一。

要求：事件数较小的地点 的事件数。
数据范围不大，考虑枚举一边的事件数，并求另一边的最大值，两边取 $\min$ 即为所求。

设 $pre_{i,j}$ 表示，枚举到时间 $i$，一边线段数为 $j$ 时，另一边线段数的最大值。
转移时枚举断点 $k$，则有：

$$pre_{i,j} = \max_{k=1}^{i}\{pre _{k,j} + cnt_{k,i},\ pre_{k,j-cnt_{k,i}}\}$$

两种情况分别代表将 $[k,i]$ 添加到两边的情况。
转移的总复杂度为 $O(n^3)$。

令 $m$ 为时间的最大值，显然答案为 $\max\limits_{j=1}^{n}\{\min(pre_{m,j},j)\}$。

---

来搞子任务二。

$pre_{i,j}$，即为 $1\sim i$ 中，一边线段数为 $j$ 时，另一边线段数的最大值。
再处理一个 $suf_{i,j}$，表示 $i\sim m$ 中，一边线段数为 $j$ 时，另一边线段数的最大值。
转移方程与 $pre_{i,j}$ 类似，即为：

$$suf_{i,j} = \max_{k=i}^{m}\{suf_ {k,j} + cnt_{k,i},\ suf_{k,j-cnt_{k,i}}\}$$

此时属于 $[s_i,t_i]$ 的线段，必包含在其中同一边，但$s_i$ 之前和 $t_i$ 之后选择的线段数 均未知。
同子任务一的思路，考虑枚举线段数，并求另一集合线段数的最大值，两边取 $\min$ 即为所求。

设 $f_{l,r}$ 为保证一边必选 $[l,r]$ 中线段时，最优的答案。
枚举 $x$ 为这边中属于 $[1,l-1]$ 的线段数， $y$ 为 $[r+1,m]$ 中的线段数。

这一边线段总数即为 $x + cnt_{i,j} + y$。
另一边选择的最大个数，显然为 $pre_{l,x} + suf_{r,y}$。

则有状态转移方程：

$$f_{l,r} = \max_{x=0}^{n}\max_{y=0}^{n}\{\min(x + cnt_{l,r} + y,\ pre_{l,x} + suf_{r,y})\}$$

---

所以答案就是 $f_{s_i,t_i}$ 吗？回答是否定的。

还有一种特殊情况：
当 $[s_i,t_i]$ 被一属于同一集合的某线段包含，即存在包含询问区间的线段时，上述 $pre_{l,x} + suf_{r,y}$ 的计算方法就不合适了。
考虑枚举这样的线段，以包含所有特殊情况。

显然，第 $i$ 个事件必选的答案即为：$\max\limits_{l=1}^{s_i}\max\limits_{l=t_i}^{m}f_{l,r}$。
这样就必须预处理出所有 $f_{i,j}$，其复杂度达到 $O(n^4)$，会被卡掉。

---

考虑一波优化。

显然， $pre_{l,x}$ 随 $x$ 的增加而减小，$suf_{r,y}$ 随 $y$ 的增加而减小。
当一边选的多了，另一边选择的余地自然少。

观察上面的式子，答案即最大的 $\min(x + cnt_{l,r} + y,\ pre_{l,x} + suf_{r,y})$，考虑如何最大化它的值。

当 $x$ 固定时，$x + cnt_{l,r}$ 与 $pre_{l,x}$ 均不变。
正序枚举 $y$，$suf_{r,x}$ 递减。此时 有$(x + cnt_{l,r} + y)\uparrow$ 而 $(pre_{l,x} + suf_{r,y})\downarrow$。
讨论一波，显然有下图形式：

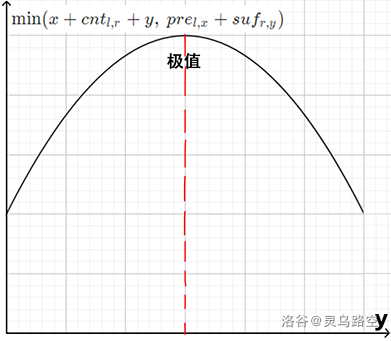
它是一关于 $y$ 的单峰函数。在峰值左侧有 $x + cnt_{l,r} + y< pre_{l,x} + suf_{r,y}$，函数递增。右侧则相反。

---

当 $x$ 增加时，$x + cnt_{l,r}$ 增加，$pre_{l,x}$ 减小。单峰函数的极值会在 $y$ 更小时取到，有：

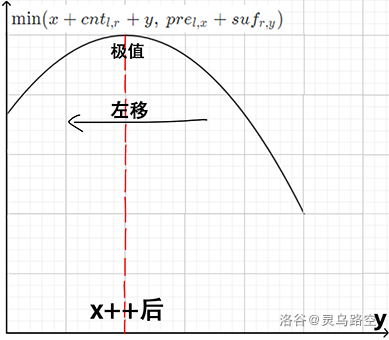
发现 在 $x$ 增加时，令答案更优的 $y$ 单调递减。

则可在正序枚举 $x$ 的同时，设立一指针指向 最优的 $y$，单调左移即可。
省去一层循环，复杂度 $O(n^3)$，期望得分 $100\text{pts}$。

调了很久发现是离散化挂掉了
代码 P1973 [NOI2011]NOI 嘉年华 - Luckyblock

P1270 “访问”美术馆

树形 DP。

先扒茬扒茬性质：

1. 到达一个房间的路径只有一条，显然屋子呈一树形结构，且只有到达叶节点才有贡献。
2. 没有给出具体房间个数，但总时间 $T \le 600s$，可知节点数较少。
3. 在警察赶来之前 逃走，则花费时间 $< T$

先 dfs 建树，考虑树形 DP。

令 $f_{u,i}$ 表示，在根节点为 $u$ 的子树中，取得 $i$ 幅画并回到 节点 $u$ 的最小时间花费。变成了一个树形背包问题，暴力求解即可，边界为 $f_{u,0} = 0$，有：

$$f_{u,i} = \min_{j=1}^{}\{f_{u,i-k} + f_{v,k} + 2\times (u,v)\}$$

对于叶节点，有：

$$f_{u,i} = 5\times i$$

注意转移时不可直接更新 $f_{u,i}$，会造成以新换新。
倒序枚举 $i$，使 $f_{root,i}<T$ 的第一个 $i$ 即为答案。

由于是二叉树，复杂度为 $O(n^3)$ 级别，期望得分 $100\text{pts}$。

---

发现是优美的二叉树，做树形背包小题大做了。
可直接枚举 左右儿子中选择的数量来更新答案。
有：

$$f_{u,i} = \min\{f_{v1,j} + 2\times (u,v_1) + f_{v2,i-j}+2\times (u,v_2)\}$$

复杂度 $O(n^3)$ 级别，期望得分 $100\text{pts}$。

代码 P1270 “访问”美术馆 - Luckyblock

P2577 [ZJOI2004]午餐

线性 DP，排序。

设第 $i$ 个人打饭时间，吃饭时间分别为 $a_i$ 与 $b_i$，前 $i$ 个人打饭时间总和为 $sum_i$。

先考虑 只排一队 的情况，对于一给定的队列完成的时间，有：

$$time = \max_{i=1}^{n}\{sum_i+b_i\}$$

考虑两个相邻的人 $i$ 与 $i+1$，若有 $b_{i+1} > b_i$：

• 当 $i+1$ 在后面时，两者完成时间分别为：

  $$\begin{aligned} & sum_{i-1} + (a_i + b_i)\\ & sum_{i-1} + a_i + (a_{i+1}+b_{i+1}) \end{aligned}$$

  显然第 $i+1$ 个人一定后吃完，即有下式成立：

  $$sum_{i-1} + a_i +(a_{i+1}+b_{i+1})> sum_{i-1} + (a_i + b_i)$$

• 当 $i+1$ 在前面时，完成时间分别为：

  $$\begin{aligned} & sum_{i-1}+ (a_{i+1} + b_{i+1})\\ & sum_{i-1} + a_{i+1}+ (a_i + b_i) \end{aligned}$$

  两人吃完的先后顺序不定。

显然有：

$$\begin{aligned} & sum_{i-1} + a_i +(a_{i+1}+b_{i+1})> \\ & \max\{sum_{i-1}+ (a_{i+1} + b_{i+1}), sum_{i-1} + a_{i+1}+ (a_i + b_i)\} \end{aligned}$$

---

则欲使 $\max\limits_{i=1}^{n}\{sum_i+b_i\}$ 尽可能小，令$i+1$ 排在前面更优。感性理解一下，吃饭慢的放在前面一定更优。
则可先将 $n$ 个人按照吃饭时间降序排序，逐个加入队列的人变成有序的了。可以考虑线性 DP 求解此题。

发现有两边，不好设状态。
考虑 P1973 的思路，枚举一边的答案，并求另一边答案的最小值，两边取 $max$ 即为所求。
设 $f_{i,j,k}$ 表示 $1\sim i$ 中，窗口一最后一个人为 $j$，完成时间为 $k$ 时，窗口二的完成时间。

然后发现无法转移，因为最后一个人不一定 最晚吃完。
陷入思考...

手搓的心心.png

发现窗口二的队列，必定为窗口一的补集。

设当前第 $i$ 个人加入队列，令窗口一队列 打饭时间总和为 $j$，则窗口二 打饭时间 总和为 $sum_i - j$。

若已知 $j$，则可计算第 $i$ 个人加入窗口 一/二 的 完成时间。
考虑枚举窗口一打饭时间总和 $j$，来更新答案。

---

设 $f_{i,j}$ 表示，前 $i$ 个人加入队列，窗口一队列打饭时间总和为 $j$时，两窗口的最小完成时间。

考虑第 $i$ 个人排到窗口 一/二：

1. 排到窗口一，则有：
   $$f_{i,j} = \max\{j + b_i,\ f_{i-1,j-a_i}\}$$
   $j + b_i$ 为新加入窗口一的人的完成时间。
   $f_{i-1,j-a_i}$ 为：不加此人时，窗口一的完成时间 与 窗口二的完成时间 的最小值，用于更新答案，不会导致漏解。
2. 排到窗口二，则有：
   $$f_{i,j} = \max\{f_{i-1,j},\ sum_i-j+b_i\}$$
   $sum_i-j+b_i$ 为新加入窗口二的人的完成时间。
   $f_{i-1,j}$ 也为不加此人时，窗口一的完成时间 与 窗口二的完成时间 的最小值。

上述两种情况取最小值即可。
复杂度 $O(nT)$ ($T$ 为最大时间)，期望得分 $100\text{pts}$。

代码 P2577 [ZJOI2004]午餐 - Luckyblock

P2501 [HAOI2006]数字序列

线性 DP，构造。

太妙了，学到虚脱.

题意简述

给定一长度为 $n$ 的数列 $a$，可将 $a_i$ 改为任意整数 $k$，代价为 $\mid a_i -k\mid$。
求使数列变为单调严格上升序列，最少需要改变的个数。
及改变数最少时，最小的代价和。
$1\le n\le 3.5\times 10^4, 1\le a_i\le 10^5$。

先搞掉第一问。

需要改变最少，则需保留得尽可能多。
考虑保留两个数的条件，对于 $a_i,a_j(i < j)$，若可保留，说明 $a_i < a_j$ 且改变 $[i+1,j-1]$ 内的数，可使序列 $[i,j]$ 严格上升。

如数列 $1, 4, 5, 3$ (无歧义)，虽然满足 $1<3$，但它们中间的两个数无论改成多少，都无法满足单增性质。

显然保留 $a_i,a_j$ 的条件为：$a_j-a_i \ge j-i$。
移项，得 $a_j - j \ge a_i - i$。
发现保留 $a_i$ 的条件为 $a_i-i$ 单调不降。

设 $b_i = a_i - i$。
使用经典 $O(n\log n)$ 的方法，求数列 $b$ 的最长不下降子序列长度，即为答案。

---

来搞第二问。

发现使 $a_i$ 单调上升的代价，等价于使 $b_i$ 单调不降的代价。
有个结论：
对于区间 $[l,r]$，使其单调不降，则存在分界点 $k$，使 $b_i = b_l(i\le k), b_j = b_r (j>k)$，此时代价最小。

如何证明这个听起来很扯皮的结论？

考虑做第一问时，顺便维护一下每个数的从哪里转移而来。
设转移前驱为 $pre_i$。
显然，$pre_i$ 为满足 $b_i \ge b_{pre_i}$ 的，且使子序列最长的位置。
则不存在 $pre_i<j<i$，使 $b_j\le b_i$，否则 $pre_i = j$ 显然更优。

考虑 $pre_i$ 和 $b_i$ 之间的数 $b_j$，一定满足 $b_j < b_{pre_i}$ 或 $b_j>b_i$，它们一定要被修改。
设 $b_j$ 修改后为 $c_j$，显然 $c_j$ 单调不降，且 $b_{pre_i} \le c_j\le b_i$。
则有下图形式：

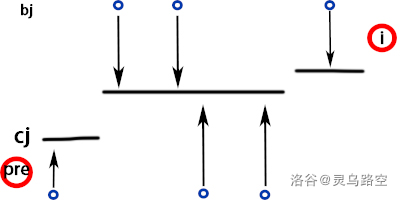
上图给出了一种修改的方案，考虑能否调整方案，使答案更优。
分类讨论：
对于一段被改为 $c$ 的连续区间 $[l,r]$：

1. 若 $b_j < b_{pre_i}$ 的数量大于 $b_j > b_{pre_i}$ 的数量，则 $c$ 越小，代价越小。
   又要保证单调不降，则 $c = c_{l-1}$ 时最优。
2. 若 数量相反，分析过程同上，$c = c_{r+1}$ 时最优。
3. 若 数量相等，$c$ 可取任意值。

则可对此方案进行调整：

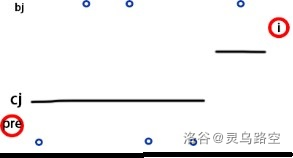
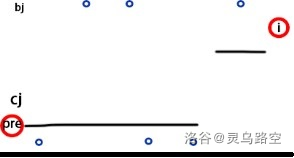
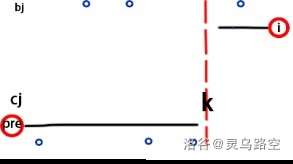
发现满足结论形式，则对于任意不满足结论的方案，均可进行调整，使代价更小，最终必定调整至结论中的形式。

令 $g_i$ 表示，最后一位是 $b_i$ 时单调不降的代价。
枚举满足条件的前驱 $pre$，转移 $b_i$，
枚举的前缀满足：

• $pre_i < i, b_{pre}\le b_i$。
• 以$b_{pre}$结尾的 最长不降子序列长度 = 以 $b_i$ 结尾的 - 1。

之后枚举分界 $k$，求得最小的代价。
有：

$$g_i = \min\{g_{pre} + \sum_{j=pre+1}^{k}\mid b_j-b_{pre}\mid + \sum_{j=k+1}^{i-1}\mid b_j-b_{i}\mid\}$$

后面那一大堆 $\sum$ 可以用前缀后缀和优化。
复杂度 $O(n^2)$ 级别？但数据随机，$[pre_i,i]$ 的长度较小，可以跑过去。

代码中用 vector 记录长度为 $i$ 的最长不降子序列的结尾，再通过判断确定转移前缀。
$from$ 表示转移前缀，$pre$ 表示前缀和。
注意不开 long long 爆零两行泪。

代码 P2501 [HAOI2006]数字序列 - Luckyblock

P4158 [SCOI2009]粉刷匠

线性 DP。

？这波算是大暴力草了过去

给定一 $N\times M$ 的空白矩阵，以及每个格子的目标颜色（为只能为红 / 蓝）。
每次可选择一行上连续的一段，涂上一种颜色。
每个格子最多只能被粉刷一次。
可涂色 $T$ 次，求最多正确粉刷的个数。
$1\le N,M\le 500,0\le T\le 2500$。

注意 每个格子最多只能被粉刷一次。
由于这个性质，一个格子不会被多次更改颜色。
无后效性，可考虑线性 DP。

一开始没注意到，往区间 DP 往上莽了一阵

---

先考虑一行的情况：

把红色格子当作 0，蓝色看成 1。
显然一段连续同色区段，可以一次涂完。
考虑将连续同色区段合并，如下图形式：

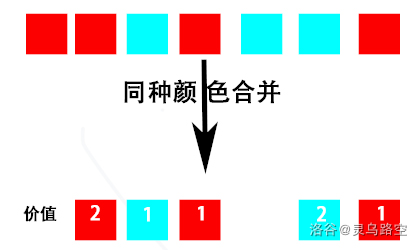
发现合并后的一行变成 0/1 交替的形式。
上一个格子与这一个目标状态一定不同。
以下提到格子，均指合并后的格子。

考虑新加入一个格子 $i$，对花费的影响。
由上，影响新格子的，只有最后一个格子的状态。

1. 当上一个格子刷错时，可顺便刷对新格子，花费不变。
2. 当上一个格子刷对时，要想刷对新格子，必须多花费一次。
3. 当上一个格子刷对时，刷错新格子，总花费不变。
4. 当上一个格子刷错时，刷错新格子，必须多花费一次。

格子刷错对答案无贡献，刷对时对答案贡献为 $val_i$

设 $f_{i,j,k, 0/1}$ 表示，第 $i$ 行，在 $1\sim j$ 中刷 $k$ 次，第 $j$ 个格子刷 错/对时，能刷对的最多格子数。
设 $val_{i,j}$ 为格子 $(i,j)$ 的权值，显然有：

$$\begin{aligned} &f_{i,j,0} = \max\{f_{i,j-1,k,1},\ f_{i,j-1,k-1,0}\}\\ &f_{i,j,1} = \max\{f_{i,j-1,k,0},\ f_{i,j-1,k-1,1}\}+val_{i,j} \end{aligned}$$

合并后每行格子长度变小，复杂度上限 $O(nmT)$。

---

显然，第 $i$ 行刷 $j$ 次后，能刷对的最多格子数为：

$$val_{i,j} = \max\{f_{i,n,k,0}, f_{i,n,k,1}\}$$

每行只能做一次贡献，涂色总次数为 $T$，自此变成了一个分组背包问题。

数据范围较小，可暴力 $O(nT^2)$ 实现。
直接暴力显然显然过不去，加个小剪枝，使每行涂色数 $\le$ 格子数即可。

代码中数组 $val$ 有两种含义，注意重新赋值时含义的变化。
代码 P4158 [SCOI2009]粉刷匠 - Luckyblock

P1295 [TJOI2011]书架

线段树优化 DP。

双倍经验 P1848 [USACO12OPEN]Bookshelf G。
这边有 dalao 的神仙题解。

？我一开始为什么要写二维 DP

给出一个长度为 $n$ 的序列 $h$。
将 $h$ 分成若干段，满足每段数字之和都不超过 $m$。
最小化每段的最大值之和。
$1\le n\le 10^5, 1\le h_i\le 10^9$

有个非常显然的 DP ：
设 $f_i$ 表示，已经分好 $i$ 个数字的最小代价。
转移时枚举这一段的开头 $k$，将 $[k,i]$ 作为新的一段，则有：

$$f_i = \min\{f_{k-1} +\max_{j=k}^{i}h_j\}\ (\sum_{k}^{i}h_i\le m)$$

暴力 DP 复杂度 $O(n^2)$，期望得分 $30\text{pts}$。
实际上能水 $50\text{pts}$（大雾

考虑优化。

显然，对于一个给定的 $i$，当 $k$ 单增时，$\max\limits_{j=k}^{i}h_j$ 单调不增，$f_{k-1}$ 单调不降。
当枚举到 $i$ 时，$f_{k-1}$ 不会再改变，考虑 $h_i$ 对 $\max\limits_{j=k}^{i}h_j$ 的影响。

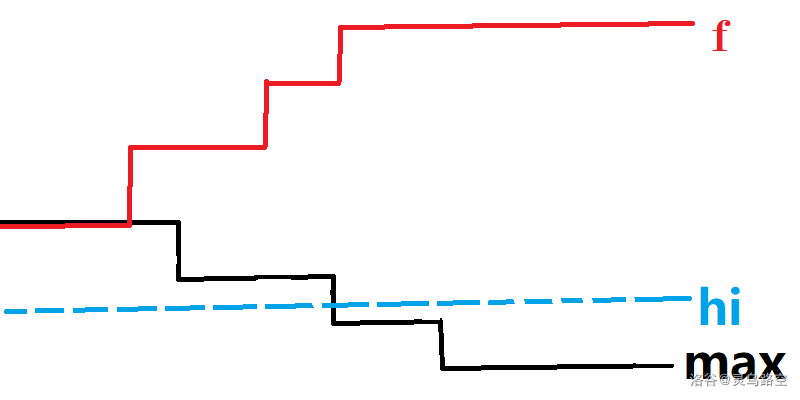
如图，设 $i$ 左侧第一个满足 $h > h_i$ 的位置为 $pre_i$，显然 $\max\limits_{j=k}^{i}h_j(k> pre_i)$ 都会变为 $h_i$。

$\max\limits_{j=k}^{i}h_j$ 可用支持区间赋值的数据结构进行维护，转移 $f_i$ 时，需要进行区间查询。
考虑线段树。

---

线段树维护位置 $k$ 的 $f_{k-1}$ 和 $f_k+\max\limits_{j=k}^{i} h_j$。
当枚举到一个新的 $h_i$ 时：

1. 单点修改，更新位置 $k=i$ 时的 $f_{k-1}$。
2. 根据 $h_i$ 更新区间 $[pre_{i}+1,i]$ 的 $f_k+\max\limits_{j=k+1}^{i} h_j$。
3. 二分得到 第一个不满足 $\sum\limits_{k}^{i}h_i\le m$ 的位置 $l$，则 $k\in [l+1,i]$。
4. 查询 $[l+1,i]$ 中最小的 $f_{k-1} + \max\limits_{j=k}^{i}h_j$。

复杂度 $O(n\log n)$，期望得分 $100\text{pts}$。

代码 P1295 [TJOI2011]书架 - Luckyblock

P1052 过河

线性 DP，神奇优化。

题意简述

给定一数轴，标号 $0\sim L$。
从 $0$ 出发，每次可向右移动 $S\sim T$ 个单位。
数轴上有 $M$ 个点，求移动到数轴外，经过的最少的点数。
$1\le M\le 100,\ 1 \le L\le 10^9, 1\le S\le T\le 10$。

算法一

我会暴力！
设 $f_i$ 表示，到达 $i$ 时，经过的最少的点数。
令 $a_i$ 表示位置为 $i$ 的点的数量，则有：

$$f_i = \min_{j=i-T}^{i-S}\{f_j + a_i\}$$

$S,T$ 较小，可看做常数，复杂度 $O(L)$ 级别。
期望得分 $30\text{pts}$。

---

算法二

发现 $M \le 100$，但 $L\le 10^9$。
数轴上有大段的空白区域没有点存在，这些位置对答案无贡献。
而算法一中仍然在这些位置进行了转移，浪费了大量时间。

当 $S < T$ 时：
发现有很多移动距离，都可以凑出来。
这个问题类似 Noip2017 D1T1 小凯的疑惑。
如 $S=5, T=6$ 时，最大的凑不出来的距离为 $19$，比 $19$ 更大的距离均可凑出来。

考虑两个距离过大的点。
显然，从左边的点出发，最大的凑不出来的距离 右侧的位置（包括右侧的点），均可通过凑距离到达。

而两个点之间的位置 对答案无贡献。
在不影响 可到达性的同时，可考虑将两点距离缩小。
缩小到仍出现 上述任意点可到达的情况，不影响答案。
以下有两种缩法：

1. $2520$ 缩，由于 $\operatorname{lcm}(1\sim 10) = 2520$，距离为 $2520$ 时，必然出现上述情况。
2. $71$ 缩， $9,10$ 凑不出来的最大距离为 $9 \times 10 - 9 - 10 = 71$，则距离 $71$ 是出现上述情况的最小值。

题解中神仙们给了缩距离的详细证明 Luogu题解。

复杂度 $O(kM)$ ($k$ 为缩成的距离)，期望得分 $100\text{pts}$。

---

WA 成 80 了。

发现算法二并不适用于 $S=T$ 的情况。
$S=T$ 时，移动路径已知，先后经过 $S,2S,...,kS$ 这些点。
则 位置为 $S$ 的倍数的点的数量 即为答案。

代码 P1052 过河 - Luckyblock。

P2051 [AHOI2009]中国象棋

线性 DP，状压。

题意简述

给定一张 $N\times M$ 的棋盘。
求每一行，每一列棋子数 $<3$ 的方案数。
$1\le N,M \le 100$。

合法的一行最多只有 $2$ 个棋子，且只能放在棋子数 $<2$ 的列上。
当枚举到第 $i$ 行时，棋子数相等的两列是等价的，棋子的位置并没有影响。
考虑枚举 每种棋子数的列数，及这 $2$ 个棋子的位置进行转移。

设 $f_{i,j,k}$ 表示，前 $i$ 行，有 $j$ 列有 $1$ 个棋子，$k$ 列有两个棋子，合法的方案数。
显然有 $m-j-k$ 列没有棋子。

考虑放棋子的个数：

1. 不放时，贡献为 $f_{i-1,j,k}$。
2. 放一个时：
   • 放到没有棋子的一列，会使棋子为 $1$ 的列数 + 1。
     有 $m-(j-1)-k$ 行没有棋子，则有这些种放置方案。
     则贡献为 $f_{i-1,j-1,k}\times (m-(j-1)-k)$。
   • 放到棋子数为 $1$ 的一列，会使棋子为 $1$ 的列数 - 1，会使棋子为 $2$ 的列数 + 1。
     有 $j+1$ 种放置方案，则贡献为 $f_{i-1,j+1,k-1}\times (j+1)$。
3. 放两个时：
   • 都放到没有棋子的列，贡献为 $f_{i-1,j-2,k}\times C((m-(j-2)-k),2)$。
   • 都放在有 $1$ 个棋子的列，贡献为 $f_{i-1,j+2,k-2} \times C(j+2,2)$。
   • 一个放在有棋子的一列，一个放在有 $1$ 个棋子的一列。
     此时棋子数为 $1$ 的列数不变。
     贡献为 $f_{i-1,j,k-1} \times j \times (m-(j-1)-k)$。

贡献求和，即为 $f_{i,j,k}$ 的值。

代码 P2051 [AHOI2009]中国象棋 - Luckyblock

CF79D Password

差分，状压 DP。

双倍经验 P3943 星空。
将此题代码交过去可直接 AC，但 P3943 数据较弱，没有卡掉错误的背包解法。
完全背包解法错误原因 详见 题解 P3943 【星空】 - Epworth 的博客。

给定一长度为 $n$ 的 $0$ 串，给定 $k$ 个 位置。
给出 $m$ 个长度 $b_i$，每次可选择一段长度为 $b_i$ 的子序列取反。
求使 $k$ 个位置变为 $1$ ，其他位置仍为 $0$ 的最小步数。
$1\le n\le 10^4,\ 1\le m\le 100,\ 1\le b_i\le n,\ k\le 10$。

发现题目等价于 一开始只有 $k$ 个位置开着灯，使所有灯都关上的最小步数。
设关灯为 $0$，开灯为 $1$，以下均按照上述等价情况展开。

看到区间修改，考虑差分。但此题为区间取反，一般的作差差分无法使用，考虑异或差分。
令 $b_i = a_i\ \text{xor}\ a_{i+1}$，对于样例 1，有：

差分前	$\ \ 1 1 1 0 1 1 1 1 1 0$
差分后	$10011000010$

在差分后数组前添加一个 $0$ 位置。
手玩后发现，差分后必然有偶数个 $1$ 出现。

此时若进行区间取反，只会使区间两端位置改变，中间不变。
若将原序列中 $1\sim 3$ 取反，则有：

差分前	$\ \ 0 0 0 0 1 1 1 1 1 0$
差分后	$00001000010$

发现只有 $0,3$ 两个位置的 $1$ 被改变。

则问题转化为：

给定一有 $2k$ 个位置为 $1$ 的 01 串。
每次可选择一对距离为 $b_i$ 的位置，将其取反。
求将其变为 $0$ 串的最小步数。

分类讨论，进行下一步转化：

1. 将一对 $0$ 取反，显然会使答案更劣，不可能发生。
2. 将一个 $0$ 一个 $1$ 取反，可看做原有的 $1$ 移动至 $0$ 的位置。
3. 将一对 $1$ 取反，可看做一个 $1$ 移动到另一个的位置，两个 $1$ 碰撞变成 $0$。

一定会发生偶数次 两个 $1$ 碰撞的情况。考虑每次使两个 $1$ 碰撞的最小代价。
若已知两个 $1$ 的位置为 $u,v$，使其碰撞的代价即 使用 $b_i$ 和 $-b_i$ 凑出 $v - u$ 的步数。显然可以 bfs 预处理出碰撞每对 $1$ 的花费。

问题转化为：

给定 $2k$ 个物品，每次可取出一对物品。
取出每对物品的花费已知，求全取出的最小花费。

由于 $k\le 10$，显然可以压缩 $k$ 个物品选/不选的状态。
接下来就是个很简单的状压了。
每次枚举两个不在集合中的物品 加入集合转移即可。

代码 CF79D Password - Luckyblock

P1040 加分二叉树

区间 DP。

一个 $n$ 个节点的二叉树的中序遍历为 $1,2,\dots n$。，每个节点都有一个分数 $w_i$。
定义一颗子树的加分为：根的左子树的加分 $\times$ 根的右子树的加分 $+$ 根的分数，空子树的加分为 $1$。
求二叉树的最高加分，及此时的前序遍历。
$n\le 30, w_i < 100$。

有个中序遍历的性质：
中序遍历可看做 “拍扁序”，
其每一个子序列 都表示 树联通的一部分。

显然 每一个子序列都满足最优子结构性质。
可求出其最优组成结构，接到其他部分上。
考虑 DP。

设 $f_{l,r}$ 表示子序列 $[l,r]$ 构成的树的最大加分。
对于空子树的情况，初始化 $f_{i,i-1} = 1$。
考虑枚举根 $k$ 进行转移，则有：

$$f_{l,r} = \max_{k=l}^{r}\{f_{l,k-1} \times f_{k+1,r} + val_k\}$$

可通过 区间 DP / 记忆化搜索实现。

由于要输出前序遍历，考虑维护 $root_{l,r}$ 表示最大加分时 $[l,r]$ 的根。
在更新 $f_{l,r}$ 时顺便维护，输出时递归输出即可。

代码 P1040 加分二叉树 - Luckyblock。

P1273 有线电视网

树形 DP，树上背包。

题意简述

给定一棵根节点为 $1$，节点数为 $n$ 的树，边有边权。
有 $m$ 个叶节点，叶节点有点权。
选择一棵以 $1$ 为根的子树，使选择的边权值 $\le$ 点权值。
最大化选择的叶节点的数量。
$1\le m<n \le 3000$。

显然可以树形 DP，考虑状态设计。
设状态记录 选择的叶节点的个数时，无法处理边权值 $\le$ 点权值的限制。
移项有：点权值 $-$ 边权值 $\ge 0$，考虑记录 点权值 $-$ 边权值的大小。

设 $f_{i,j}$ 表示，以 $i$ 为根的子树中选择了 $j$ 个叶节点时，点权值 $-$ 边权值最大值。
显然，答案为满足 $f_{1,j} \ge 0$ 的 $j$ 的最大值。

有转移方程：

$$f_{u,j} = \max_{k=0}^{size_v} \{f_{u,j-k} +f_{v,k} - w_{u,v}\}$$

表示从 $v$ 的子树中取出 $k$ 个子节点加入 $u$ 的子树中，同时计算 $u,v$ 边权的贡献。
$size_v$ 为 子树 $v$ 中叶节点的个数。

可将从 $v$ 中取出 $1,2,\dots k$ 个叶节点的贡献，看做 $k$ 个体积分别为 $1\sim k$ 的，不同的物品。
$v$ 只能做一次贡献，是一个显然的分组背包问题。

为防止重复贡献，枚举 $j$ 时应倒序枚举。

代码 P1273 有线电视网 - Luckyblock。

P3287 [SCOI2014]方伯伯的玉米田

结论，树状数组优化 DP。

题意简述

给定一长度为 $n$ 的序列 $a$，可进行最多 $k$ 次区间 $+1$ 操作。
求操作后的最长不下降子序列长度。
$1<n<10000, 1< k\le 500, 1\le a_i \le 5000$。

先猜个结论：所有修改操作的右端点一定为 $n$。

设修改区间为 $[l,r]$，显然修改区间内部 元素相对大小不变。
左侧元素不变，$[1,l-1]$ 的 不下降子序列 不变。
则区间增高后，$[1,r]$ 的 最长不下降子序列 长度 只会增不会减。

而 右侧元素不变，区间增高后，可能无法接到 $[l,r]$ 元素的后面，会导致 最长不下降子序列 减小。
为保证答案最优，则应使 $r = n$。

---

有了这个结论就可以暴力转移了。
设 $f_{i,j}$ 表示，以位置 $i$ 结尾，$i$ 已经被 $j$ 个区间覆盖时，$[1, n]$ 中最长不下降子序列长度，则有：

$$\large f_{i,j} = \max_{1\le k<i,\ 0\le l\le j,\ a_k+l \le a_i+j}\{f_{k,l}\} + 1$$

复杂度 $O(n^2k^2)$，期望得分 $0\text{pts}$。

---

考虑优化。
观察状态转移方程，发现 $f_{k,l}$ 是满足 $1\le k<i,\ 0\le l\le j,\ a_k+l \le a_i+j$ 的一个三维前缀最大值。
$i$ 维可以通过枚举消除，问题变为二维前缀最大值问题。

考虑二维树状数组优化。
修改状态，设 $f_{j,k}$ 为 $1\sim i-1$ 中，被不超过 $j$ 个修改区间覆盖，结尾 $\le k$ 的最长不下降子序列的长度。
直接用树状数组维护 $f$ 即可。

注意 $j$ 可以为 $0$，树状数组的 $j$ 维整体右移一位， $j+1$ 实际上表示使用了 $j$ 次修改。

由于通过枚举消除了 $i$，为防止重复更新，套用01背包的思想，$j$ 需要从大到小枚举。

复杂度 $O(nk\log n\log k)$，期望得分 $100\text{pts}$。

---

神仙提出的单 $\log$ 写法：

观察状态的含义：
$f_{j,k}$ 为 $1\sim i-1$ 中，被不超过 $j$ 个修改区间覆盖，结尾 $\le k$ 的最长不下降子序列的长度。
发现 $j$ 固定时，$f_{j,k}$ 随 $k$ 增加，只增不减。
发现 $k$ 固定时，$f_{j,k}$ 随 $j$ 增加，只增不减。

则树状数组中 $x\le j,y\le k$ 的最大值，一定会在第 $j$ 行/ 第 $k$ 列取到。

考虑建立 $2$ 个 $n$ 行的一维树状数组，分别维护每行/每列的 $f$ 值，更新时更新 整行/整列 有下图形式：

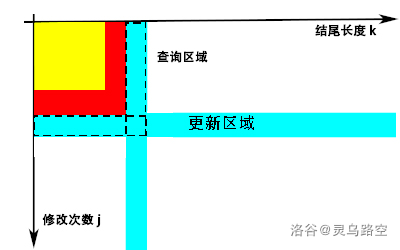
复杂度 $O(nk\log n)$，期望得分 $100\text{pts}$。

代码 P3287 [SCOI2014]方伯伯的玉米田 - Luckyblock

P2487 [SDOI2011]拦截导弹

Cdq 分治优化 DP。

2020.9.5 偷偷回来更新一下没人发现吧

题意简述

给定一长度为 $n$ 的序列，序列中元素 $i$ 有两个属性 $h_i,v_i$。
选择一个子序列 $b$，满足 $h_{b_i} \le h_{b_j}, v_{b_i} \le v_{b_j}(j<i)$。
求满足条件的子序列的最长长度。
若从所有 满足条件且长度最长的子序列中随机选择一个，求所有元素能够出现在子序列中的概率。
$1\le n\le 5\times 10^4$，$1\le h_i, v_i\le 10^9$。

二维 LIS 问题。

设 $f1_i$ 为以元素 $i$ 为结尾的 LIS 的长度，$g1_i$ 表示这样的 LIS 的个数。
则有一个显然的暴力：

$$f1_i = 1 + \max_{j=1}^{i-1} f1_j[h_j\ge h_i][v_j\ge v_i]$$

$$g1_i = \sum_{j=1}^{i-1} g1_j [h_j\ge h_i][v_j\ge v_i][f1_j + 1 = f1_i]$$

第一问答案即为 $\max\limits_{i=1}^{n} f1_i$。

考虑第二问，设$f2_i$ 为以元素 $i$ 为开头的 LIS 的长度，$g2_i$ 表示这样的 LIS 的个数。
将原序列翻转，再做一遍上面的 DP 即可更新 $f2, g2$。
若元素 $i$ 出现在整个序列的 LIS 中，则必有：

$$f1_i + f2_{n-i+1} - 1 = \max_{i=1}^{n} f1_i$$

表示 LIS 可以通过包含 $i$ 的两端拼接而成。
此时元素 $i$ 能够出现在子序列中的概率 即为 $\dfrac{g1_i\times g2_i}{\sum\limits_{i=1}^{n}{g1_i}}$。
否则概率为 $0$。

复杂度 $O(n^2)$，期望得分 $30\text{pts}$。

---

总共有 $O(n^2)$ 对转移，跑不过，考虑优化。
观察上述转移方程，能够用来更新 $f_i$ 的 $f_j$ 必须满足 $j<i, h_j\ge h_i, v_j\ge v_i$。
是一个三维偏序的形式，考虑 Cdq 分治。

考虑 $O(n^2)$ 对转移，将其看作 $O(n^2)$ 个点对。
设当前处理的区间为 $[l, r]$，考虑Cdq 分治的一般过程：

1. 若 $l = r$，返回。
2. 设区间中点为 $mid$，递归处理 $[l,mid]$ 和 $[mid + 1, r]$。
3. 计算横跨 $mid$ 的转移的贡献。

计算贡献时，套路地维护双指针，并用线段树维护 $f$ 的前缀最大值 和 $g$ 的前缀和。

---

但是这样有问题。
通过 Cdq 改变了转移顺序，不能保证递归 $[mid + 1, r]$ 时所有的 $f_i(i<mid + 1)$ 都被更新过。
考虑改变分治的过程：

1. 若 $l = r$，返回。
2. 设区间中点为 $mid$，递归处理 $[l,mid]$。
3. 计算横跨 $mid$ 的转移的贡献。
4. 递归处理 $[mid + 1, r]$。

正确性？
观察 Cdq 的递归树。

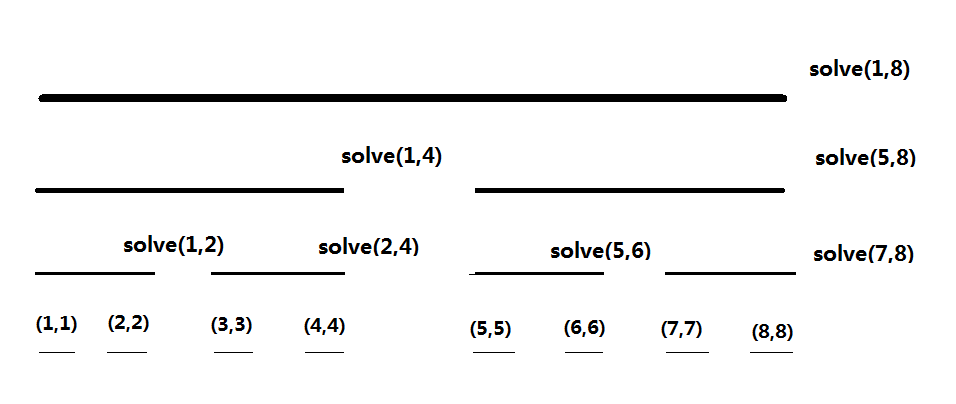
在更新 $[mid + 1, r]$ 之前，$[l, mid]$ 的 DP 值均已更新完毕。
考虑横跨 $mid$ 的转移，发现则 $mid + 1$ 的 DP 值一定会被更新到。

考虑 $[mid + 1, r]$ 的递归过程，会先递归到 $[mid + 1, mid + 2]$。
在计算横跨 $mid + 1$ 的转移时，$mid + 2$ 的 DP 值也会被更新。
返回上一层 $[mid + 1, mid + 4]$，$[mid + 1, mid + 2]$ 的 DP 值均已更新完毕。
又回到了一开始的形式，以此类推即可。

---

一点小 Trick

关于 Cdq 改变处理顺序的一点小 Trick。

三维偏序中的 Cdq 是这样的：

void Cdq(int l_, int r_) {
  if (l_ == r_) return ;
  Cdq(l_, mid), Cdq(mid + 1, r_);
  Solve(); //处理横跨 mid 的点对
}

本题的 Cdq 理论上应该是这样的：

void Cdq(int l_, int r_) {
  if (l_ == r_) return ;
  Cdq(l_, mid);
  Solve();
  Cdq(mid + 1, r_);
}

如果仅仅这样写的话，会 WA 穿掉。
原因是在 Solve 中，序列的顺序会发生变化。
可能会使 $[mid + 1, r]$ 不满足应有的单调性，接下来递归处理的时候会出错。
应该加个排序，写成这样：

void Cdq(int l_, int r_) {
  if (l_ == r_) return ;
  sort(l_, r_);
  Cdq(l_, mid);
  Solve();
  Cdq(mid + 1, r_);
}

注意每次考虑横跨 $mid$ 的转移时，都将线段树清空。

线段树维护的 $f$ 中，可能有相等的 $f$。
如果它们为区间最大值，它们的出现次数应累加。

注意线段树中更新的顺序。

代码：P2487 [SDOI2011]拦截导弹 - Luckyblock

P1846 游戏

线性 DP。

2020.10.3 偷偷回来更新一下没人发现吧

考试题，场上写挂爆零了没到 300= =
写错变量名就是真的离谱。

给定两数列 $a,b$，长度分别为 $n,m$，可以做如下操作：
删除 $a$ 的最后 $x(x\ge 1)$ 个数，设其和为 $sum_a$，删除 $b$ 的最后 $y(y\ge 1)$ 个数，其花费为 $sum_b$。
该次操作的总花费为 $(sum_a - x) \times (sum_b - y)$。
一直操作到 $a,b$ 均为空，最小化所有操作的总花费。
$1\le n,m\le 2000$，$1\le a_i\le 1000$。

40pts

感谢出题人送的超高暴力分！

暴力 DP，设 $f_{i,j}$ 表示将数列 $a$ 删剩下 $i$ 个，数列 $b$ 删剩下 $j$ 个时，需要的最小的花费。
转移时枚举两数列最后一次删除的长度 $x,y$，则有很简单但是写起来很长的方程：

$$f_{i,j} = \left\{ \min_{x=1}^{n-i}\min_{y=1}^{m-j} \left(f_{i+x,j+y} + \left(\sum_{k=i+1}^{i+x}a_k - x\right) \times \left(\sum_{k=j+1}^{j+y}b_l - y\right)\right)\right\}$$

可以使用前缀和预处理 $\sum a$ 和 $\sum b$，转移复杂度 $O(n^2m2)$。
由于要保证不出现一个数列为空，一个不为空的情况，统计答案时枚举最后一次删除的长度，则有：

$$ans = \min_{i=1}^{n}\min_{j=1}^{m}\left\{ f_{i,j} + \left(\sum_{k=1}^{i} a_k - i\right) \times \left(\sum_{l=1}^{j} b_l - j\right)\right\}$$

统计答案复杂度为 $O(nm)$，总复杂度为 $O(n^2m^2)$。

---

一点性质

发现选择一个数的贡献，是该数的值，减去 1。
考虑将所有数都减去 1，转移方程变为：

$$f_{i,j} = \left\{ \min_{x=1}^{n-i}\min_{y=1}^{m-j} \left(f_{i+x,j+y} + \sum_{k=i+1}^{i+x}a_k \sum_{k=j+1}^{j+y}b_l \right)\right\}$$

转移方程会比较好写，并且减小了某些分析的难度。
以下分析均在此方程下展开。

---

60pts

一个结论：每次各删除 $a$，$b$ 中的一段数时，一定有一边删除的个数为 $1$。

是不是很扯皮？
略证，对于某次操作，设删除的部分为 $a_i \sim a_{i+x}$，$b_j \sim b_{j+y}$。删除它们的花费即为：

$$\sum_{k=i}^{i+x} a_k\sum_{l=j}^{j+y} b_l$$

设存在一组 $x',y'$，满足：$1\le x'<x$，$1\le y'<y$。
如果先删除 $a_{i+x'}\sim a_{i+x}$ 和 $b_{j+y'} \sim b_{j+y}$，再删除 $a_{i}\sim a_{i+x'-1}$ 和 $b_{j}\sim b_{j + y' - 1}$，其花费为：

$$\begin{aligned} &\sum_{k=i}^{i+x'-1} a_k\sum_{l=j}^{j+y'-1} b_l + \sum_{k=i+x'}^{i+x} a_k\sum_{l=j+y'}^{j+y} b_l\\ \le& \sum_{k=i}^{i+x} a_k\sum_{l=j}^{j+y} b_l\\ =& \left(\sum_{k=i}^{i+x'-1} a_k + \sum_{l=j}^{j+y'-1} b_l\right) \times \left(\sum_{k=i+x'}^{i+x} a_k + \sum_{l=j+y'}^{j+y} b_l\right) \end{aligned}$$

将一大段被删除的数划分成更小的段，代价一定不会更劣。
则最后一定会划分出长度为 $1$ 的删除段，结论成立。

则可修改状态转移方程，钦定一边选仅一个，仅需枚举另一边的选择个数，即仅枚举 $x$ 或 $y$。
转移复杂度变为 $O(nm(n + m))$。

---

100pts

考虑优化状态。
发现转移时需要钦定一边只选择 $1$ 个。若钦定 $a$ 仅选择 $1$ 个，有用状态的 $i'$ 均为当前状态的 $i+1$。

设 $f_{i,j}$ 表示将数列 $a$ 删剩下 $i$ 个，数列 $b$ 删剩下 $j$ 个时，且上一次删数时钦定 $a$ 删除了 $1$ 个，需要的最小花费。
同理，设 $g_{i,j}$ 表示上一次删数时钦定 $b$ 删除了 $1$ 个，需要的最小的花费。

考虑转移，以 $f_{i,j}$ 为例，分类讨论：

1. $a,b$ 均删除 $1$ 个，代价即为 $a_{i+1}\times b_{j+1}$。
   上一次删多少不受影响，显然可以从 $f_{i+1,j+1}$ 和 $g_{i+1,j+1}$ 转移而来。
   则有转移：

   $$f_{i,j} = \min\left\{ f_{i+1,j+1},g_{i+1,j+1}\right\} + a_{i+1}\times b_{j+1}$$

2. $a$ 删除 $1$ 个，$b$ 删除 $y(y>1)$ 个，则其代价为 $a_{i+1}\times \sum_{k=j+1}^{j+y} b_{k}$。
   发现代价可以拆成 $a_{i+1}\times a_{j+1} + a_{i+1} \times \sum_{k=j+2}^{j+y} b_k$。
   对于后一项，其已经被统计到 $i'=i,j'=j+1$ 的情况中了。
   则有转移：

   $$f_{i,j} = f_{i,j+1} + a_{i+1}\times b_{j+1}$$

综上，则有：

$$f_{i,j} = \min\left\{ f_{i,j+1},f_{i+1,j+1},g_{i+1,j+1}\right\} + a_{i+1}\times b_{j+1}$$

同理，对于 $g_{i,j}$，有：

$$g_{i,j} = \min\left\{ g_{i+1,j},f_{i+1,j+1},g_{i+1,j+1}\right\} + a_{i+1}\times b_{j+1}$$

每次转移是 $O(1)$ 的，转移总复杂度 $O(nm)$。
答案即为 $\min \{f_{0,0}, g_{0,0}\}$

---

为啥你的状态和别人不一样啊？

发现上面两个转移方程形式基本相同，所以可以合并状态。
就得到了其他题解的形式。

---

爆零小技巧

有些看起来无意义的状态仍然对答案有贡献。
比如当 $i,j$ 其中有一个为 $0$ 时，

代码详见：P1846 游戏 - Luckyblock

P2495 [SDOI2011]消耗战

树形 DP，虚树优化 DP。

题意简述

给定一棵 $n$ 个节点的树，边有边权。
给定 $m$ 次询问，每次给定 $k$ 个关键点，要求切除一些边，使得 $k$ 个关键点与编号为 $1$ 的点不连通。
最小化切除的边的权值之和。
$2\le n\le 2.5\times 10^5$，$1\le m\le 5\times 10^5$，$\sum k \le 5\times 10^5$，$1\le k\le n$，边权值 $w\le 10^5$。
2S，512MB。

首先想到一个简单的 DP。对于单次查询，设 $f_u$ 为令以 $u$ 为根的子树中的所有关键点 与 $u$ 不连通的最小代价。
转移时枚举 $u$ 的子节点，有状态转移方程：

$$f_{u} = \sum_{v\in son_u} \begin{cases} w(u,v) &(v\text{ is a key node})\\ \min\{w(u,v), f_v\} &\text{otherwise} \end{cases}$$

单次查询复杂度 $O(n)$，总复杂度 $O(nm)$，无法通过本题。

发现关键点集较小，不含任何关键点的子树显然无用，考虑建立虚树。
发现使得一个关键点 $u$ 与根不相连的最小代价为根到关键点路径上最短的边长，设其为 $\operatorname{val}_u$，在 dfs 时顺便维护。对于建立的虚树，有新的状态转移方程：

$$f_{u} = \sum_{v\in son'_u} \begin{cases} \operatorname{val}_v &(v\text{ is a key node})\\ \min\{\operatorname{val}_v, f_v\} &\text{otherwise} \end{cases}$$

总复杂度 $O(\sum k)$ 级别，可以通过本题。
对于本题，还可以删除以关键点作为祖先的关键点 进行进一步的优化。正确性显然，因为一定要使得其祖先与根不相连。
注意答案的最大值在 ll 范围之内，注意预处理 1 号节点到各点路径上的最短边长时，极大值的设置。

有不少细节，详见代码。
代码详见：「虚树」P2495 [SDOI2011]消耗战 - Luckyblock

拓扑序应用

DAG 上 DP。

蓝书上的题。

求一个拓扑图中从给定的 S 点到 T 点的必经边。
$O(n+m)$ 可过。

发现一条边必须经过，当且仅当出现类似下图一样 “独木桥” 的形式：

对于一条这样的边 $(u,v)$，考虑乘法原理，显然有：
从 S 到达它的方案数 $\times$ 它到达 T 的方案数 = S 到达 T 的方案数。

方案数显然可以 DP 求得。

设 $f_i$ 表示从 S 出发到达点 $i$ 的路径数量，$g_i$ 表示从点 $i$ 到达 T 的路径数量。
有显然的状态转移方程：

$$f_{i} = \sum_{(u,i) \in E} f_u$$

$$g_{i} = \sum_{(i,v) \in E} g_v$$

从 S，T 各做一次 dfs 即可求得，复杂度 $O(n)$。
$f_{T}$ 即为从 S 到达 T 的方案数。

则对于一条这样的必经边 $(u,v)$，显然有：

$$f_{u}\times g_{v} = f_{T}$$

$O(m)$ 枚举所有的边进行判断即可，算法总复杂度 $O(n + m)$。

$f,g$ 可能会很大，可以写个 Hash，对几个质数同时取模进行判断。

无代码。

P3478 [POI2008]STA-Station

树形 DP，换根 DP。

题意简述

给定一 $n$ 个结点的树，求出一个节点，使得以该节点为根时，所有节点的深度和最大。
一个节点的深度定义为该节点到根的简单路径上边的数量。
$1\le n\le 10^6$。
时限 2s，内存 128M，SPJ。

需要同时维护子树和祖先的信息，考虑换根 DP。
钦定 1 为根，第一次 dfs 处理子树信息，第二次 dfs 处理祖先信息进行换根。

先考虑子树信息，预处理出所有子树的 $size$。
设 $f_u$ 表示 $u$ 的子树中所有点到 $u$ 的距离之和，则显然有：

$$f_{u} = \sum_{fa_v = u}{\left\{f_{v} + size_v\right\}}$$

---

对于祖先的信息，考虑在第二次 dfs 中维护。
若当前 dfs 到节点 $u$，设 $val$ 表示 $u$ 上面各点到 $u$ 的距离之和。
考虑向下深入，根由 $u$ 变为 $v$ 时，对 $val$ 的影响。

先考虑哪些点在 $v$ 上方，包括 $u$ 上方的点，及 $v$ 的兄弟。
对于 $u$ 上方的点，其到 $u$ 的距离和为 $val$。
对于 $v$ 的兄弟们，其到 $u$ 的距离和为 $f_{u} - (f_{v} + size+v)$（除去 $v$ 的影响）。

对于所有上述节点，其到 $v$ 的距离等于其到 $u$ 的距离 $+1$，则新的 $val$ 还应 $+ n-size_v$。

在第二次 dfs 换根时，进行答案的判定。
答案即为 $f_u + val$ 最大的节点之一。

代码详见：P3478 [POI2008]STA-Station - Luckyblock

CF708C Centroids

树形 DP，换根 DP。

上古时期的古代人类的涂鸦。

第一次正式地接触换根 DP = =
写这么个破题写了好长时间。

另外，up and down 似乎是 cdx 时代的叫法/jk

给定一棵大小为 $n$ 树。
可以进行一种修改：删去任意一条边，再加入一条边，需保证修改后后还是一棵树。
对于每一个节点，判断进行不多于一次修改后，该点能否成为重心（若以某个点为根，每个子树的大小都不大于$\frac{n}{2}$，则称该点为重心）。
$1\le n\le 4\times 10^5$，时限 4s。

钦定 1 为根，求得所有子树的 $size$ 和 重儿子 $son$。
考虑一个本不是重心的点 $u$，以它为根时必存在一$size > \frac{n}{2}$ 的儿子。
在 dfs 的过程中考虑该子树的位置：
若该它在 $u$ 以下，则一定为重儿子 $son_u$。
否则它由 $u$ 以上树的剩余部分构成，大小为 $n - size_u$。

显然，欲使 $u$ 成为重心，必须从该大小 $>\frac{n}{2}$ 的子树取出一块。
贪心的想，最优的修改，是取出一块 $size \le \frac{n}{2}$ 的且 $size$ 最大的，直接接到 $u$ 上。
若原子树 $size$ 减去取出部分的 $size$ $\le \frac{n}{2}$，$u$ 就成为了重心。

---

需要同时维护子树和祖先的信息，考虑换根 DP。
第一次 dfs 处理子树信息，第二次 dfs 处理祖先信息进行换根。

先考虑子树信息。
设 $f_{u}$ 表示 $u$ 的 儿子 的子树中的，$size \le \frac{n}{2}$ 的子树中的，最大的 $size$。
设 $g_v$ 为 $v$ 的贡献，则显然有：

$$\begin{aligned} &g_v = \begin{cases} size_{v} &size_{v}\le \frac{n}{2}\\ {f_v} &\text{otherwise}\\ \end{cases}\\ &f_{u} = \max_{fa_v=u} \{g_v\} \end{aligned}$$

---

对于祖先的信息，考虑在第二次 dfs 中维护。
设 $val$ 表示 $u$ 以上部分中，$size \le \frac{n}{2}$ 的子树中的，最大的 $size$。
考虑向下深入，根由 $u$ 变为 $v$ 时，对 $val$ 的影响。

对于$v$ 上面部分，若 $n - size_u\le \frac{n}{2}$，则其贡献为 $n - size_u$，否则贡献为 $val$。
对于 $v$ 的兄弟 $d$，显然其贡献为 $f_d$。
贡献取 $\max$ 即为新的 $val$。

---

在第二次 dfs 换根时，进行答案的判定，则有：

$$ans_u = \begin{cases} 1 &(n-size_{u}\le \frac{n}{2}) \land (size_{son_u}\le \frac{n}{2})\\ [n-size_{u}-val \le \frac{n}{2}] &n-size_{u}\le \frac{n}{2}\\ [size_{son_u} - f_{son_u}\le \frac{n}{2}] &size_{son_u}\le \frac{n}{2}\\ \end{cases}$$

---

考虑一些奇怪的实现。

在更新 $val$ 时，提到了这样一句：「对于 $v$ 的兄弟 $d$，显然其贡献为 $f_d$」。
若直接枚举兄弟进行更新，复杂度显然无法承受。

考虑预处理，对于一个节点 $u$ 的所有儿子 $v$，考虑将所有 $f_{v_i}$ 写成一个序列。
所求即为抠去 将转移到的 $v$ 后序列的最大值，可以通过维护序列前缀 和 后缀最大值实现。
详见代码。

采用这样的实现后，总复杂度是常熟略大的 $O(n)$。

---

以上是个人的傻逼写法，看了题解之后学习了。
真的有必要维护前缀最大值，和后缀最大值吗？
显然没有必要。

若将转移到的 $f_v$ 不是最大的，则用于更新的 $f_{v_i}$ 一定是最大的。
否则则用于更新的 $f_{v_i}$，一定是次大的。
仅维护最大值和次大值即可，总复杂度不变，但常数和空间复杂度都大大减小。

代码详见：CF708C Centroids - Luckyblock

「NOI2015」寿司晚宴

状压 DP。

题目中的一句话：
寿司的美味度为从 $2$ 到 $n$。

什么是良心出题人？
这就是良心出题人！

给定 $n,p$，求：从 $2\sim n$ 取出两个集合（可以为空），使得分属两个集合中的数均互质的方案的数量 $\bmod p$。
$1\le n\le 500$，$1\le p\le 10^{10}$。
时间 1s，空间 128M。

30pts

注意以下讨论均在 $\pmod{p}$ 下展开。

定义数集 $S$ 中的数质因数分解后的质数集为 $\operatorname{P}(S)$。
显然对于集合 $S1,S2$，分属两集合中的数均互质的充要条件是 $\operatorname{P}(S1) \cap \operatorname{P}(S2) = \varnothing$。

考虑对于每一个质数集 $\operatorname{P}(S)$，求得其对应的质因数分解的集合 $S$ 的个数。
又 $n\le 30$，质数仅有 $10$ 个，考虑状压 DP。

设 $f_{i,\operatorname{P}(S)}$ 表示，由 $1\sim i$ 组成的数集 $S$ 中，$\operatorname{P}(S)=i$ 的个数。

对于 $f$，转移时使用刷表法，考虑加入数字 $i$ 的影响，枚举质数集合 $S$，则有：

$$f_{i,S|\operatorname{P}(\{i\})} = f_{i,S|\operatorname{P}(\{i\})} + f_{i-1,S}$$

统计答案时枚举两方所选质数集合 $S1,S2$。当 $S1\cap S2 = \varnothing$ 时，则有：

$$ans = ans + (f_{n,S1} \times f_{n,S2})$$

直接做空间会爆炸，需要滚动数组优化一下。
总时间复杂度 $O(n\times 2^{10} + 2^{20})$。

---

100pts

直接存质数集合存不下了。

地球人都知道整数 $i$ 至多只有一个大于 $\sqrt {i}$ 的质因子。
相同的质因子互相冲突，考虑将 $i\in [1,n]$ 按含有的大于 $\sqrt {i}$ 的质因子进行划分，对每一数段 分段 DP，再将它们合并。

DP 状态仅需记录不大于 $\sqrt{500}$ 的 $8$ 个质因子的存在状况即可。
稍微修改下定义，定义数集 $S$ 中的数质因数分解后的小于 $22$ 的质数组成的集合为 $\operatorname{P}(S)$。

设划分后的数列为 $a$，当前枚举的数段是第 $x$ 段，为 $[a_l,a_r]$，含有的大于 $22$ 的质因子为 $y$。
设 $g_{x,\operatorname{P}(S1), \operatorname{P}(S2)}$ 表示考虑到前 $x$ 段数，一方选择的集合 $S1$ 质因数分解后为 $\operatorname{P}(S1)$，另一方为 $\operatorname{P}(S2)$ 的合法的方案数量。
设 $f1_{i,\operatorname{P}(S1), \operatorname{P}(S2)}$ 表示由 $a_1\sim a_i$ 组成的数集 $S1,S2$ 中，两方分别为 $\operatorname{P}(S1)$、$\operatorname{P}(S2)$，且含有 $y$ 的数均属于 $S1$ 时合法的方案数量。
类似地，设$f2_{i,\operatorname{P}(S1), \operatorname{P}(S2)}$ 含有 $y$ 的数均属于 $S2$ 时合法的方案数量。

初始化，枚举两方所选质数集合 $S1,S2$，则有：

$$\begin{aligned} f1_{l-1,S1,S2} = g_{x-1,S1,S2}\\ f2_{l-1,S1,S2} = g_{x-1,S1,S2} \end{aligned}$$

转移时使用刷表法，考虑加入数字 $a_i$ 的影响，枚举两方所选质数集合 $S1,S2$，当 $S1\cap S2 = \varnothing$ 时，则有：

$$\begin{aligned} f1_{i,S1 | \operatorname{P}(\{a_i\}),S2} = f1_{i,S1 | \operatorname{P}(\{a_i\}),S2} + f1_{i-1,S1,S2}[\operatorname{P}(\{a_i\})\cap S2 = \varnothing]\\ f2_{i,S1,S2 | \operatorname{P}(\{a_i\})} = f2_{i,S1,S2 | \operatorname{P}(\{a_i\})} + f2_{i-1,S1,S2}[\operatorname{P}(\{a_i\})\cap S1 = \varnothing] \end{aligned}$$

分别代表将 $a_i$ 分入集合 $S1,S2$ 后的影响，注意后面的条件判断。

得到 $f$ 后，再将 $f$ 合并到 $g$ 中。
枚举两方所选质数集合 $S1,S2$，当 $S1\cap S2 = \varnothing$ 时，则有：

$$g_{x, S1,S2} = f1_{r, S1,S2} + f2_{r, S1, S2} - g_{x-1, S1,S2}$$

会出现两边都不选的情况，且一开始 $f1,f2$ 都初始化成了 $g_{x-1\cdots}$，所以需要减去算重的 $g_{x-1, S1,S2}$。

最后的答案即为 $\sum_{S1\cap S2 = \varnothing} \{g_{x,S1,S2}\}$。

直接做的空间依旧会爆炸，依旧需要滚动数组优化一下。
对每一个 $i$ 都做了一遍转移，合并的次数小于 $n$，则总时间复杂度为 $O(n 2^{16})$ 级别。

注意将数列分段后，转移后要枚举新的数列元素进行转移。

代码详见：「NOI2015」寿司晚宴 - Luckyblock。

P6858 深海少女与胖头鱼

概率期望，DP

对面有 $n$ 只带有「圣盾」的「鲭鱼圣者」，$m$ 只不带「圣盾」的「鲭鱼圣者」。
每次可以等概率地对场上一只「鲭鱼圣者」造成伤害。
「圣盾」可以抵挡一次伤害，可以立即杀死不带「圣盾」的「鲭鱼圣者」。
每当一个「鲭鱼圣者」失去「圣盾」时，其他 所有存活的「鲭鱼圣者」都会获得「圣盾」。
求杀死所有「鲭鱼圣者」的其期望攻击次数 $\bmod 998244353$ 的值。

$1\le n\le 10^{14}$，$0\le m\le 10^6$。
保证答案的形式 $\frac{p}{q}$ 满足 $(p,q\in \mathbf{N}$，$998244353\nmid q)$。
1S，128MB。

先考虑 $m=0$ 的情况，显然此时场上没有盾的鱼人最多只有 1 条。
考虑 DP，设 $f_{n,0/1}$ 表示干掉 $n$ 条带盾的鱼人，$0/1$ 条不带盾的鱼人所需攻击次数的期望。

显然有：$f_{0,0} = 0$，$f_{0,1} = 1$。

转移时考虑从一个状态攻击一次能达到的状态，有：

$$\begin{aligned} f_{i,0} &= f_{i-1,1} + 1\\ f_{i,1} &= \frac{i}{i+1} \times (f_{i,1} +1)+ \frac{1}{i+1} \times (f_{i,0} + 1) \end{aligned}$$

对于一式的情况，此时只能攻击一个带盾的鱼人，削除该鱼人的盾。其攻击次数为削除该鱼人的盾后需要的次数 + 1。

对于二式的情况，若以 $\frac{i}{i+1}$ 的概率攻击了一条带有圣盾的鱼人，还会转移到相同的状态。
若以 $\frac{1}{i+1}$ 的概率攻击了不带盾的鱼人，则会转移到削除该鱼人的状态。

---

发现上面的方程转移不来，化下二式：

$$\begin{aligned} f_{i,1} &= \frac{i}{i+1} \times (f_{i,1} +1)+ \frac{1}{i+1} \times (f_{i,0} + 1)\\ i\times f_{i,1} + f_{i,1} &= i\times f_{i,1} + f_{i,0} + i + 1\\ f_{i,1} &= f_{i,0} + i + 1 \end{aligned}$$

得到了 $f_{i,1}$ 与 $f_{i,0}$ 的关系。 再将一式代入，有：

$$f_{i,1} = f_{i-1,1} + i + 2$$

显然是一个等差数列求和的形式，由 $f_{0,1} = 1$，则有（具体推导过程见最后）：

$$\begin{aligned} f_{i,1} &= \frac{i(i+5) + 2}{2}\\ f_{i,0} &= f_{i,1} - i - 1 = \frac{i(i+3)}{2} \end{aligned}$$

预处理 2 的逆元后，可以 $O(1)$ 地求得 $m=1$ 时的答案 $f_{n,0}$ 了。

---

再推广到 $m\not = 1$ 的情况。
更一般性地，设 $f_{n,m}$ 表示干掉 $n$ 条带盾的鱼人，$m$ 条不带盾的鱼人所需攻击次数的期望。
由上显然有：

$$f_{n,m} = \dfrac{n}{n+m}\times (f_{n+m-1,1} +1) + \dfrac{m}{n+m}\times (f_{n,m-1} + 1)$$

上式中的前一项 $f_{n+m-1,1}$ 可以 $O(1)$ 求，后面一项可以递推。
每次都 $O(\log p)$ 地求逆元，总复杂度 $O(m\log p)$。

---

等差数列求和公式：

$$\begin{aligned} S_n &= \frac{n(a_1+a_n)}{2}\\ &= na_1 + \frac{n(n-1)d}{2} \end{aligned}$$

注意 $n\le 10^{18}$，需要先令 $n\bmod 998244353$，否则必爆 LL。

代码详见：P6858 深海少女与胖头鱼 - Luckyblock

P3786 萃香抱西瓜

状压 DP，分层图，最短路

题意简述

无法简述的题面。

稍有点细节的状压 DP。

读入时对所有时刻所有位置进行标记，记录是否有大小西瓜。

发现小西瓜个数较小，考虑状压一下获得的小西瓜状态。
设 $s_{t,x,y}$ 表示 $t$ 时刻，位置 $(x,y)$ 的小西瓜的存在状态。
设 $f(t, x, y, S)$ 表示，在时间 $t$，萃香的位置在 $(x,y)$，获得的小西瓜状态为 $S$ 时，需要移动的最小步数。

初始化 $f(1, sx, sy, s_{1,sx,sy}) = 0$，所有不可到达状态的 $f = \operatorname{Inf}$。

转移时枚举每个时刻每个位置，从能到达该位置的上个时刻的位置 $(x',y')$ 转移过来，还需要枚举上个位置的小西瓜状态，有：

$$f(t,x,y,S|s_{t,x,y}) = \min\{f(t-1,x',y', S)\} + 1$$

统计答案时枚举最后一个时刻的所有取完所有小西瓜的状态，取最小值即可。

复杂度 $O(Thw2^m)$，数据范围小可以随便过。

代码详见：P3786 萃香抱西瓜 - Luckyblock

CF1437C Chef Monocarp

线性 DP。

$q$ 组数据，每次有 $n$ 道菜在一个炉中，第 $i$ 道菜的最佳取出时间为 $t_i$。
若一道菜在时间 $T$ 被取出，定义它的「不中吃度」为 $|T-t_i|$。
每一时刻只能取出一道菜，求将所有菜取出的最小「不中吃度」之和。
$1\le q\le 200$，$1\le t_i\le n\le 200$。
2S，256MB。

发现一些显然的结论。

• 依次取出的菜的 $t_i$ 一定是递增的，证明考虑反证法，可知交换两道菜顺序后答案不会更优。
• 由于 $t_i\le n$，则取出最后一道菜的时间 $T< 2n$。

则先将 $t$ 升序排序，取菜的顺序已经确定，考虑给每一道菜确定一个最优的取出时间。
考虑 DP，设 $f_{i,j}$ 表示在前 $j$ 个时刻，已经取出前 $i$ 道菜的最小「不中吃度」之和。

初始化 $f_{0,i} = 0$，其他 $f=\infin$。

转移时考虑取出第 $i$ 道菜的时间，显然有：

$$f_{i,j} = \min{\{f_{i,j-1},\ f_{i-1,j-1} + |t_i-j|\}}$$

注意这是一个前缀 DP 值，因此需要继承上一个时刻的信息。

显然答案即为 $f_{n,2n-1}$。
总时间复杂度 $O(qn^2)$。

代码详见：一场 CF。

CF1437E Make It Increasing

线性 DP，分段 DP。

给定一长度为 $n$ 的数列 $a$，大小为 $k$ 的集合 $b$。
对于任意 $x\notin b$，可将 $a_x$ 修改为任意整数。
判断是否可以将数列变为单调递增，若可以则输出最小修改次数。
$1\le b_i\le n\le 5\times 10^5$，$0\le k\le n$，$1\le a_i\le 10^9$。
2S，256MB。

这题很眼熟，先考虑 $k=0$ 的情况，就是这个题了：P2501 [HAOI2006]数字序列。

需要改变最少，则需保留得尽可能多。
考虑保留两个数的条件，对于 $a_i,a_j(i < j)$，若可保留，说明 $a_i < a_j$ 且改变 $[i+1,j-1]$ 内的数，可使序列 $[i,j]$ 严格上升。
显然保留 $a_i,a_j$ 的条件为：$a_j-a_i \ge j-i$。
移项，得 $a_j - j \ge a_i - i$，发现保留 $a_i$ 的条件为 $a_i-i$ 单调不降。
设 $c_i = a_i - i$，需要改变的次数即为 $n - \operatorname{LNDS}(c)$，$O(n\log n)$ 求解即可。

再考虑限制，发现被限制位置划分出的每一段都是相互独立的。
对于一段划分出的区间 $[l,r]$ 仅需保证每一段的 $\operatorname{LNDS}$ 的元素大小均在 $[c_l,c_r]$ 中即可。由上显然有 $c_l>c_r$ 时无解。
对每一段分别计算代价即可，时间复杂度仍为 $O(n\log n)$。

代码详见：一场 CF。

CF1437F Emotional Fishermen

线性 DP，组合数学。

给定一长度为 $n$ 的数列 $a$，求有多少个 $1\sim n$ 的排列 $p$，满足：

$$\forall i\in [1,n],\ \dfrac{a_{p_i}}{\max_{1\le j<i}{\{a_{p_j}\}}} \notin \left(\frac{1}{2}, 2\right)$$

答案对 $998244353$ 取模。
$2\le n\le 5\times 10^3$，$1\le a_i\le 10^9$。
4S，1G。

这个范围和时限显然是想让选手 $O(n^2)$ 草过去。

考虑一个合法的排列 $p$ 中 $a_i$ 的前缀最大值，显然它是单调不降的，且存在下列形式：

$$a_{p_x} \cdots a_{p_y} \cdots a_{p_z}\cdots$$

且满足 $\forall i<y, 2a_{p_i}\le a_{p_y}$，$\forall i<z, 2a_{p_i}\le a_{p_z}$。

容易发现，若两个排列中这样的分界元素 $a_{p_?}$ 不同，则两个排列一定不同。
考虑求用这样的分界元素构建排列 $p$ 的方案数。

为了方便，先将 $a$ 升序排序。
设 $f_{i}$ 表示当前填入排列的最大分界元素为 $a_i$ 的填充方案数。
预处理 $\operatorname{lim}_{i}$ 表示满足 $2a_j \le a_i$ 的 $j$ 的数量。

转移时考虑填入的上一个分界元素 $a_j$（显然有 $j\in [1,\operatorname{lim}_i]$)，并将 所有能填 的元素填入，则有：

$$f_{i} = \sum_{j=0}^{\operatorname{lim}_i} f_j\times A(n - 2 - \operatorname{lim}_j,\ \operatorname{lim}_i - \operatorname{lim}_j - 1)$$

解释一下：

• 对于 $f_j$，它表示填入了前 $\operatorname{lim_j}$ 个数和 $a_j$ 的方案数。
• $n - 2 - \operatorname{lim}_j$ 表示在 $f_j$ 的基础上填入 $a_i$ 后剩下的空位数。
• $\operatorname{lim}_i - \operatorname{lim}_j - 1$ 表示在上述基础上还需要填入的数的个数，即 $\operatorname{lim}_i$ 中未填的数的个数。

总时间复杂度 $O(n^2)$。

注意预处理阶乘的逆元，否则会 T。

官方题解还有一种二维状态的不一样的做法：Tutorial。

代码详见：一场 CF。

CF1433F Zero Remainder Sum

线性 DP。

给定一 $n\times m$ 的数字矩阵 $a$，参数 $k$。
要求在矩阵中选择一些数，使得每行选择的数量不超过 $\frac{m}{2}$，且数的总和是 $k$ 的倍数。
最大化选择的数的和。
$1\le n,m,k, a_{i,j}\le 70$。
1S，256MB。

这数据范围显然是给 $O(n^4)$ 草的，考虑暴力 DP。
设 $f_{i,j,cnt,r}$ 表示第 $i$ 行，考虑到第 $j$ 个数，选择了 $cnt$ 个数，选择的数之和 $\bmod k = r$ 时，选择的数之和的最大值。

初始化 $f_{i,j,0,0} = 0$，其他 $f = -\infin$。
转移时暴力转移即可，有：

$$f_{i,j,cnt,r} = \max{\{f_{i,j-1,cnt,r},\ f_{i,j-1,cnt-1,(r-a_{i,j})\bmod k} + a_{i,j}\}}$$

再设 $g_{i,j}$ 表示在前 $i$ 行选出了一些数，选择的数之和 $\bmod k = j$ 时，选择的数之和的最大值。

初始化 $g_{0,0} = 0$，其他 $g = -\infin$。
转移时枚举第 $i$ 行选数的情况，暴力转移，有：

$$g_{i,j} = \max{\{g_{i-1, (j-f_{i,m,cnt, r})\bmod k} + f_{i,m,cnt, r}\}}$$

发现 $f$ 的第一维并没有什么用，实现时删除即可。
最后的答案即为 $g_{n,0}$。

总时间复杂度 $O(n^4)$。

代码详见：另一场 CF。

「CSP-S 2020」函数调用

DAG 上 DP，倒序枚举。

又臭又长的题面。

先根据拓扑序记忆化搜索，求得每个操作 3 的乘法增量 mul，即会令各元素变为之前的多少倍。
完成上述过程后，可顺便得到乘法操作对原数的影响。

再考虑加法操作，再在拓扑序上 DP，求得每种操作被调用多少次，注意 倒序 进行，通过调用者更新被调用者。
某加法操作的贡献为调用次数 + 影响到它乘法操作的次数。
两者贡献量相同，在代码中用 cnt 记录了两者的和。

最后还原原数即可，时间复杂度 $O(n+m)$。

代码详见：CSP 2020-S 题解 - Luckyblock

P3558 [POI2013]BAJ-Bytecomputer

结论，线性 DP。

题意简述

给定一只包含 $-1.0,1$ 的数列 $a$，每次操作可令 $a_{i} + a_{i-1}$。
判断能否使该序列单调不降，若可以则求所需的最少操作次数。
$1\le n\le 10^6$，$|a_i|\le 1$。
1S，128MB。

发现一些结论：

• 显然应该从前往后操作。
• 若某位置为 $1$，则经过若干次操作后它之后的位置都可以 $\ge 1$。
• 若某位置为 $-1$，则经过若干次操作后它之后的位置都可以 $\le -1$。
• 由上述结论可知，若出现：$0,\cdots, 0, -1,\cdots$ 的情况，则一定无解，否则一定有解。
• 显然最终答案一定是 $-1\cdots, -1,0,\cdots,0,1$ 的形式，不可能出现 $|a_i|\ge 2$ 的情况。 因为 $-2$ 只能通过 $-1-1$ 得到，此时已经单调不降了，变为 $-2$ 一定不优。$2$ 同理。

根据结论 4 判下无解，由结论 5，考虑 DP。
设 $f_{i,-1/0/1}$ 表示当前操作到第 $i$ 个数，第 $i$ 个数变为 $-1/0/1$ 时，令前 $i$ 个数单调不降的最小操作次数。
初始化 $f_{1,a_1} = 0$，转移时分类讨论：

$$\begin{aligned} f_{i,-1} &= \begin{cases} f_{i-1,-1} &(a_i = -1)\\ f_{i-1,-1} + 1 &(a_i = 0)\\ f_{i-1,-1} + 2 &(a_i = 1) \end{cases}\\ f_{i,0} &= \begin{cases} \min(f_{i-1,-1}, f_{i-1,0}) &(a_{i}=0)\\ f_{i-1,-1} + 1 &(a_{i} = 1) \end{cases}\\ f_{i,1} &= \begin{cases} f_{i-1,1} + 2 &(a_i = -1)\\ f_{i-1,1} + 1 &(a_i = 0)\\ \min(f_{i-1,-1},f_{i-1,0},f_{i-1,1}) &(a_i = 1) \end{cases} \end{aligned}$$

答案即 $\min(f_{n,-1},f_{n,0},f_{n,1})$。

总时间复杂度 $O(n)$。

代码详见：P3558 [POI2013]BAJ-Bytecomputer - Luckyblock。

CF1436D Bandit in a City

树形 DP

给定一棵 $n$ 个节点的有根树，根为 $1$，第 $i$ 个节点上有 $a_i$ 个人。
每个人可以往任意子节点走，直到走到叶节点，求最后人最多的叶节点的最少人数。
$2\le n\le 2\times 10^5$，$0\le a_i\le 10^9$。
1S，256MB

设 $\operatorname{sum}_{u}$ 表示 $u$ 子树中所有节点的人数之和，$\operatorname{leaf}_u$ 表示 $u$ 子树中叶节点的个数。
首先考虑最理想状态，对于节点 $u$，若它子树中的所有人都能均匀地散布在所有叶节点中，则显然该子树中 人最多的叶节点的人数为 $\left\lceil \frac{\operatorname{sum}_u}{\operatorname{leaf}_u} \right\rceil$。

但一般无法达到理想状态，设 $f_{u}$ 表示以 $u$ 为根的子树中人最多的叶节点的人数。对于节点 $u$ 的某儿子 $v$，显然，存在 $f_{v} > \left\lceil \frac{\operatorname{sum}_u}{\operatorname{leaf}_u} \right\rceil$ 时无法均分。
反之，当 $\forall v\in son(u),\ f_v\le \left\lceil \frac{\operatorname{sum}_u}{\operatorname{leaf}_u} \right\rceil$ 时，可以将 $a_u$ 按一定方案分配到各叶节点，形成均匀散布的形式。

对于所有叶节点 $u$，初始化 $\operatorname{leaf}_u = 1$，则有显然的状态转移方程：

$$\begin{aligned} \operatorname{sum}_u &= a_u + \sum_{v\in son(u)} \operatorname{sum}_v\\ \operatorname{leaf}_u &= \sum_{v\in son(u)} \operatorname{leaf}_v\\ f_{u} &= \max\left\{ \max_{v\in son(u)}\{f_v\},\ \left\lceil \frac{\operatorname{sum}_u}{\operatorname{leaf}_u} \right\rceil\right\} \end{aligned}$$

答案即为 $f_1$。

算法总时间复杂度 $O(n)$。

还有种被卡 ull 的暴力二分答案，可以参考其他题解。

代码详见：CF1436D Bandit in a City - Luckyblock。

CF1422E Minlexes

线性 DP。

给定一只由小写字母组成的字符串 $s$，可以先删除任意个 两相邻相同字符，再把剩下的部分拼接起来。
对于 $s$ 的每个后缀，求进行上述操作后得到的字典序最小的字符串。
$1\le |s|\le 10^5$。

发现是先删除再拼接，满足无后效性。考虑倒序枚举字符串 DP。
设 $f_i$ 表示后缀 $[i,|s|]$ 操作后得到的字典序最小的字符串。
初始化 $f_{|s|} = s_{|s|}$。
转移时考虑当前字符能否与上个字符相等，分类讨论：

• 若 $s_i \not= s_{i+1}$，则 $f_{i} = f_{i+1}$。
• 若 $s_{i}=s_{i+1}$，且 $s_i < f_{i+2,0}$，则接上该字符后字典序会变小，则 $f_{i} = s_{i} + s_{i+1} + f_{i+2}$。
• 若 $s_{i}=s_{i+1}$，且 $s_{i}=f_{i+2,0}$，出现了连续相等的情况。此时需要比较 $s_i$ 与 $f_{i+2}$ 从头数第 2 种字符 与 第一种字符（即 $s_i$）的大小关系。
  若第二种字符 $>s_i$，显然应该接上，则 $f_{i} = s_{i} + s_{i+1} + f_{i+2}$。
  否则应该删去，有 $f_{i} = f_{i + 2}$。

实现时用个结构体存一下 $f$ 的前后缀，便于输出。
复杂度 $O(n)$。

代码详见：再来一场 CF。

CF1457C Bouncing Ball

Link。

$t$ 组数据，每次给定一长度为 $n$ 的 01 序列，参数 $p,k,x,y$，有两种操作：

1. 花费 $x$ 的代价，使得序列中任意一个 0 变为 1。
2. 花费 $y$ 的代价，删除序列第一个元素，序列长度 $- 1$，第 $2\sim n$ 个元素向前移动一位。

求使得 $\forall q\in \mathbb{Z},\ p+qk\le n,\ a_{p+qk} = 1$ 的最小代价。
$1\le t\le 100$，$1\le p\le n\le 10^5$，$1\le k\le n$，$\sum n\le 10^5$。
1S，256MB。

线性 DP。

猜俩结论，显然操作 1 仅会修改对答案有贡献的位置。且操作的顺序一定是若干次操作 2 加上若干次操作 1。
第二个结论正确性显然，若先进行一次操作 1 再进行操作 2，之前修改的 1 可能会移动到对答案没有贡献的位置上。不如先进行操作 2，再仅修改对答案有贡献的位置。

数据范围不大，考虑枚举操作 2 进行的次数 $i$，新的对答案有贡献的位置为初始序列的 $(p + i) + qk$。
发现步长没有改变，考虑预处理 $f_{j}$ 表示 $(p+i) = j$ 时，有贡献位置上 $0$ 的个数，显然有：

$$f_{j} = \begin{cases} [a_j = 0] &(j + k >n)\\ f_{j + k} + [a_j=0] &(j + k\le n) \end{cases}$$

则操作 2 进行 $i$ 次的最小代价为 $f_{p+i}\times x + i\times y$，取最小值即为答案。
总时间复杂度 $O(n)$。

代码详见：Codeforces Round #687 - Luckyblock。

P2943 [USACO09MAR]Cleaning Up G

给定一长度为 $n$ 的数列 $a$，给定参数 $m$，满足 $1\le a_i\le m$。
要求将其划分为任意段，每段的代价为该段内权值种类数的平方。
最小化代价之和。
$1\le a_i\le m\le n\le 4\times 10^4$。
1S，128MB。

40pts

显然 DP，设 $f_{i}$ 表示划分 $1\sim i$ 的最小代价之和。
每个数都分一段代价最大，初始化 $\forall 1\le i\le n,\ f_{i} = i$，转移时枚举最后一段，则有：

$$f_{i} = \min_{j=1}^{i - 1} \left\{ f_{j} + \left| \bigcup_{k=j +1}^{i} \{a_i\}\right|^2\right\}$$

答案即 $f_n$。
预处理区间权值种类数，总复杂度 $O(n^2)$ 级别。

---

100 pts

由于分段的最大代价为 $n$，则不可能存在一段的权值种类数 $\sqrt n$。
则上述转移方程中 $\left| \bigcup_{k=j +1}^{i} \{a_i\}\right|\ge \sqrt n$ 的转移都是无用的，可以考虑仅记录有贡献的转移前驱。
考虑在枚举 $i$ 的同时维护 $\operatorname{pos}_{j}$，记录满足 $[\operatorname{pos}_j,i]$ 中有 $j$ 种权值的最左侧的位置，转移方程变为：

$$f_i = \min_{j=1}^{\sqrt n} \left\{ f_{\operatorname{pos}_j} + j^2\right\}$$

转移的时间复杂度为 $O(n\sqrt n)$。

---

再考虑如何维护 $\operatorname{pos}$，考虑维护 $\sqrt n$ 个计数数组 $\operatorname{cnt}$，第 $j$ 个计数数组维护有 $j$ 种权值的区间 $[\operatorname{pos}, i]$ 内各种的权值的个数。
每次更新 $i$ 后，考虑将 $a_i$ 加入所有计数数组后产生的影响。对于 $\operatorname{cnt}_j$，讨论一下：

• 当 $a_i$ 在 $\operatorname{cnt}_j$ 中出现过，不会影响权值种类数。
• 当 $a_i$ 未出现过，且区间权值种类数 $\ge j$，则令 $\operatorname{pos}_j$ 不断右移，直至 $\operatorname{cnt}_j$ 中出现新的一种权值的数量为零，以保证权值种类数为 $j$。

$\operatorname{pos}$ 仅会右移 $n$ 次，显然上述维护过程的总时空复杂度均为 $O(n\sqrt n)$。
程序总时空复杂度均为 $O(n\sqrt n)$。

代码详见：P2943 [USACO09MAR]Cleaning Up G - Luckyblock

「SCOI2009」Windy 数

数位 DP

给定参数 $l,r$，求 $[l,r]$ 中不含前导零且相邻两个数字之差至少为 $2$ 的正整数的个数。
$1\le l\le r\le 2\times 10^9$。
1S，512MB。

这是一个经典的数位 DP 的例子。其模型一般是给定一些对于数的限制条件，求在给定范围内满足限制的数的贡献。
通过数位 DP 一般可以在 $O(m\log_{10}{(n)})$ 的时间内解决此问题，其中 $m$ 是数码种类数，$n$ 是取值的最大值。
首先将询问 $[l,r]$ 内合法的数的个数拆成询问 $[0\sim l-1]$ 和 $[0, r]$ 内合法的数的个数，之后考虑数位 DP。先考虑爆搜。考虑枚举所有范围内的数，搜索的同时检查是否满足给定的限制条件。注意考虑前导零与是否达到枚举的上界。
发现当枚举的数前缀的性质相同，即 dfs 的四个参数相同时，dfs 的返回值相同。比如当枚举到 $020\underline{?}??$ 和 $010\underline{?}??$ 时，dfs 的参数均为 (4, 0, false, false)。表示它们前缀的性质相同，枚举之后位数得到的答案显然也相同。简单记忆化即可避免重复枚举过程。

代码详见：「笔记」数位DP - Luckyblock。

P4081 [USACO17DEC]Standing Out from the Herd P

广义 SAM 上 DP

给定 $n$ 个仅包含小写字母的字符串 $S_1\sim S_n$。
定义字符串 $S_i$ 的 「独特值」为只属于该串的本质不同的非空子串的个数。
求字符串 $S_1\sim S_n$ 的「独特值」。
$1\le n\le 10^5, 1\le \sum|S_i|\le 10^5$。
1S，128MB。

考虑在线建立广义 SAM，构建时记 $\operatorname{only}_i$ 表示状态 $i$ 包含哪一个串的信息。特别地，若某状态包含多个串信息，则$\operatorname{only}_i = - 1$。
parent 树上 DP 更新祖先信息得到 $\operatorname{only}$ 后，直接遍历所有状态，若存在 $\operatorname{only}_i \not= -1$，则令 $ans _{\operatorname{only}_i}$ 加上 $\operatorname{len}(i)-\operatorname{len}(\operatorname{link}(i))$即可。
复杂度 $O(\sum|S_i|)$ 级别。

代码详见：「笔记」广义后缀自动机 - Luckyblock

「HAOI2016」找相同字符

广义 SAM 上 DP

给定两字符串 $S_1, S_2$，求出在两字符串中各取一个子串，使得这两个子串相同的方案数。
两方案不同当且仅当这两个子串中有一个位置不同。
$1\le |S_1|, |S_2|\le 2\times 10^5$。
1S，256MB。

用两个字符串构造广义 SAM，维护每个状态维护了几个串的 $\operatorname{endpos}$。
当一个状态同时维护了两个串的 $\operatorname{endpos}$，则该状态及其 parent 树上的祖先 所代表的串，均为公共子串。

设 $size(u,0/1)$ 表示状态 $u$ 维护了串 1/2 的 $\operatorname{endpos}$ 的个数，有：

$$\sum size(i,0)\times size(i,1)\times (\operatorname{len}(i)-\operatorname{len}(\operatorname{link}(i))$$

具体地，每插入串 $i$ 的一个新字符，就对该字符对应的状态的 $size(i) +1$，在 parent 树上求子树 $size$ 和，最后枚举状态更新答案。

总复杂度 $O(|S|)$ 级别，为保证复杂度需要使用计数排序。

代码详见：「笔记」广义后缀自动机 - Luckyblock。

「AHOI2009」同类分布

枚举，数位 DP

给定两个正整数 $a$ 和 $b$，求在 $[a,b]$ 中的所有整数中，各位数之和能整除原数的数的个数。
$1\le a\le b\le 10^{18}$。
3S，512MB。

考虑到各位数之和与原数在 dfs 中都是变量，不易检验合法性。但发现各位数之和不大于 $9\times 12$，考虑先枚举各位数之和，再在 dfs 时维护前缀的余数，以检查是否合法。
同样设 Dfs(int now_, int sum_, int p_, bool zero_, bool lim_, int val_)，其中 $\operatorname{sum}$ 为前缀的各数位之和，$p$ 为原数模 $\operatorname{val}$ 的余数。
边界是搜索到第 $\operatorname{length}+1$ 位，此时返回 $[\operatorname{sum}=\operatorname{val} \land \, p = 0]$。
对数位和和余数简单记忆化即可，总复杂度 $O(2\cdot10^2\log_{10}^3(n))$ 级别。

代码详见：「笔记」数位DP - Luckyblock。

「AHOI2013」 差异

后缀树上 DP

给定一长度为 $n$ 的字符串 $S$，令 $T_i$ 表示从第 $i$ 个字符开始的后缀，求：

$$\sum_{1\le i<j\le n}\{\operatorname{len}(T_i) +\operatorname{len}(T_j) - 2\times \operatorname{lcp} (T_i,T_j)\}$$

$\operatorname{len}(a)$ 表示字符串 $a$ 的长度，$\operatorname{lcp}(a,b)$ 表示字符串 $a,b$ 的最长公共前缀长度。
$1\le n\le 5\times 10^5$。
1S，512MB。

这个式子玩意长得就很树上差分。
对于 $S$ 的后缀树，$\operatorname{lcp}$ 即为后缀树的 $\operatorname{lca}$，则上式等价于后缀树上所有后缀之间的距离之和。
则树上某一点的对答案贡献，即它的 $\operatorname{dep}$ 乘上以它为 $\operatorname{lca}$ 的后缀节点的数量。记录子树大小，DP 实现即可。

总复杂度 $O(n)$ 级别。

无代码。

「JSOI2007」文本生成器

AC 自动机上 DP。

给定 $n$ 个只由大写字母构成的模式串 $s_1\sim s_n$，给定参数 $m$。
求有多少个长度为 $m$ 的只由大写字母构成的字符串，满足其中至少有一个给定的模式串，答案对 $10^4 + 7$ 取模。
$1\le n\le 60$，$1\le |s_i|,m\le 100$。
1S，128MB。

先建立 ACAM，建 Trie 图的时候顺便标记所有包含模式串的状态。记这些状态构成集合 $\mathbf{S}$。

发现不好处理含有多个模式串的情况，考虑补集转化，答案为所有串的个数 $26^{m}$ 减去不含模式串的串个数。
考虑 ACAM 上 DP。设 $f_{i,j}$ 表示长度为 $i$，在 ACAM 上匹配的结束状态为 $j$，不含模式串的字符串的个数。
初始化空串 $f_{0,0} = 1$。转移时枚举串长，状态，转移函数，避免转移到包含模式串的状态，有：

$$f_{i,j} = \begin{cases} &\sum\limits_{\operatorname{trans}(u, k) = j} f_{i-1, u} &(j\notin \mathbf{S})\\ &0 &(j\in \mathbf{S}) \end{cases}$$

注意转移时需要枚举空串的状态 0。实现时滚动数组 + 填表即可。
记 Trie 的大小为 $|T|$，答案即为：

$$26^m - \sum_{i=0}^{|T|} f_{m,i} \pmod{10^4+7}$$

总时间复杂度 $O(m|T||\sum|)$ 级别。

---

为什么可以这样转移？

可以发现建立 Trie 图后，这个转移过程就相当于字符串的匹配过程。
可以认为 DP 过程是通过所有长度为 $i-1$ 的字符串在 ACAM 上做匹配，从而得到长度为 $i$ 的字符串对应的状态。

代码详见：「JSOI2007」文本生成器 - Luckyblock。

「SDOI2014」数数

AC 自动机上 DP，数位 DP。

给定一个整数 $n$，一大小为 $m$ 的数字串集合 $s$。
求不以 $s$ 中任意一个数字串作为子串的，不大于 $n$ 的数字的个数。
$1\le n\le 10^{1201}$，$1\le m\le 100$，$1\le \sum |s_i|\le 1500$。$n$ 没有前导零，$s_i$ 可能存在前导零。
1S，128MB。

题目要求不以 $s$ 中任意一个数字串作为子串，想到这题：「JSOI2007」文本生成器。首先套路地对给定集合的串构建 ACAM，并在 ACAM 上标记所有包含集合内的子串的状态。
之后考虑在 ACAM 上模拟串匹配的过程做数位 DP。发现前缀所在状态储存了前缀的所有信息，可以将其作为 dfs 的参数。
设 Dfs(int now_, int pos_, bool zero_, bool lim_) { 表示前缀匹配到的 ACAM 的状态为 $\operatorname{pos}$ 时，合法的数字的数量。转移时沿 ACAM 上的转移函数转移，避免转移到被标记的状态。
存在 $\operatorname{trans}(0, 0) = 0$，这样直接 dfs 也能顺便处理不同长度的数字串。
总复杂度 $O(\log_{10}(n)\sum |s_i|)$ 级别。

代码详见：「SDOI2014」数数 - Luckyblock。

「BJOI2019」奥术神杖

01 分数规划，AC 自动机上 DP。

给定一只由数字和$\texttt{.}$构成的字符串 $s$。给定 $m$ 个特殊串 $t_{1}\sim t_{m}$，$t_i$ 的权值为 $v_i$。
需要在 $s$ 中为$\texttt{.}$的位置上填入数字，一种填入方案的价值定义为：

$$\sqrt[c]{\prod_{i=1}^{c} w_i}$$

其中 $w$ 表示在该填入方案中，出现过的特殊串的价值的可重集合，其大小为 $c$。

每个位置填入的数字任意，最大化填入方案的价值，并输出任意一个方案。
$1\le m,|s|,\sum|t_i|\le 1501$，$1\le v_i\le 10^9$。
1S，512MB。

对于两种填入方案，我们只关心它们价值的相对大小。带着根号不易比较大小，套路地取个对数，之后化下式子：

$$\begin{aligned} \large \log {\sqrt[c]{\prod_{i=1}^{c} w_i}} =& \dfrac{\log {\left(\prod\limits_{i=1}^{c} w_i\right)}}{c}\\ =& \dfrac{\sum\limits_{i=1}^{c} \log {w_i}}{c} \end{aligned}$$

这是一个显然的 01 分数规划的形态，考虑二分答案。存在一种填入方案价值不小于 $mid$ 的充要条件为：

$$\begin{aligned} \dfrac{\sum\limits_{i=1}^{c} \log {w_i}}{c}\ge mid \iff \sum\limits_{i=1}^{c}\left(\log {w_i} - mid\right)\ge 0 \end{aligned}$$

---

考虑 DP 检查二分量 $mid$ 是否合法。
具体地，先将特殊串 $t_i$ 的权值设为 $\log v_i - mid$，更新 ACAM 上各状态的权值，之后在 ACAM 上模拟匹配过程套路 DP。
设 $f_{i,j}$ 表示长度为 $i$，在 ACAM 上匹配的结束状态为 $j$ 的串的最大价值。
初始化 $f_{0,0} = 0$，转移时枚举串长，状态，转移函数。注意某一位不为$\texttt{.}$时转移函数只能为串中的字符，则有：

$$f_{i,j} = \begin{cases} \max\limits_{\operatorname{trans}(u, s_i) = j} f_{i-1, u} + \operatorname{val}_{j} &(s_i\not= \texttt{.})\\ \max\limits_{\operatorname{trans}(u, k) = j} f_{i-1, u} + \operatorname{val}_{j} &(s_i= \texttt{.}) \end{cases}$$

注意记录转移时的前驱与转移函数，根据前驱还原出方案即可。
总复杂度 $O(\left(10|s|\cdot\sum |t_i|\right)\log w)$ 级别，$\log w$ 为二分次数。

代码详见：「BJOI2019」奥术神杖 - Luckyblock。

「HEOI2014」大工程

虚树，DP
我个人十分痛恨这种多合一的题目。
*这简直野蛮至极*

给定一棵 $n$ 个节点的树，边权均为 1。
给定 $m$ 次询问，每次给定 $k$ 个关键点，求 $k$ 个点对之间的路径长度和、最短路径长度、最长路径长度。
$1\le n\le 10^6$，$1\le m\le 5\times 10^4$，$\sum k \le 2\times n$。
2S，256MB。

先建立虚树，维护各点的深度，之后简单 DP。
第 2、3 问简单维护子树内关键点到根的最长链/最短链即可，考虑如何做第 1 问。
设 $f_u$ 表示以 $u$ 为根的子树内关键点对的路径长度之和，$g_u$ 表示以 $u$ 为根的子树内关键节点到 $u$ 的距离之和，$\operatorname{size}_u$ 表示以 $u$ 为根的子树内关键节点的个数。
转移时分路径在子树内/跨越根节点讨论，则有显然的转移方程：

$$\begin{aligned} f_u &= \sum_{v\in son'_u} f_v + (g_v + \operatorname{size}_v\times \operatorname{dis}(u, v))\times (\operatorname{size}_u - \operatorname{size}_v)\\ g_u &= \sum_{v\in son'_u} g_v + \operatorname{size}_v \times \operatorname{dis}(u,v)\\ \operatorname{size}_u &= [u\text{ is a key node}] + \sum_{v\in son'_u} \operatorname{size}_v \end{aligned}$$

其中 $\operatorname{dis}(u,v) = \operatorname{dep}_v - \operatorname{dep}_u$。
代码实现中使用了树链剖分，总复杂度 $O(\sum k\log n)$ 级别。

细节比较多，代码详见：「HEOI2014」大工程 - Luckyblock。

P2900 [USACO08MAR]Land Acquisition G

斜率优化 DP，$k_i$、$x_i$ 均单调，单调队列。

给定无序的 $n$ 个物品，第 $i$ 个物品有两个属性，可以表示为 $(A_i,B_i)$。
要求将这一列物品分成若干段集合，对于分出的一个集合 $S = \{(A_i, B_i)\}$，其代价为 $\left(\max_{(A_i, B_i)\in S} A_i\right)\cdot \left(\max_{(A_i, B_i)\in S} B_i\right)$，求划分的最小代价之和。
$1\le n\le 5\times 10^4$，$1\le L,c_i\le 10^6$。
1S，128MB。

纯暴力对正解并没有什么启发性，这里直接快进到如何斜率优化。

物品无序，考虑钦定一种物品的排列顺序，使得按此顺序划分时转移方程中出现乘积项。考虑将物品按 $A_i$ 降序为第一优先级，$B_i$ 升序为第二优先级排序，此时对于连续的一段 $[l,r]$，其中 $\max A_i$ 一定为 $A_l$，但 $\max B$ 不确定。此时考虑通过削除无贡献元素使得第二维也存在单调性，使得 $\max B_i$ 一定为 $B_r$。代码如下所示：

void Init() {
  n = read();
  for (int i = 1; i <= n; ++ i) a[i] = (Data) {read(), read()};
  std::sort(a + 1, a + n + 1, CMP);
  int tmp = 0;
  for (int i = 1; i <= n; ++ i) { //去除无贡献元素
    if (a[i].b > a[tmp].b) a[++ tmp] = a[i];
  }
  n = tmp;
}

此时对于划分出的一段 $[l,r]$，其代价为 $A_l\cdot B_r$。考虑朴素 DP，设 $f_i$ 表示按此顺序划分前 $i$ 个物品的最小代价和，转移时枚举上一段的结尾，则有：

$$f_i = \min_{j=0}^{i-1}\left\{ f_j + A_{j + 1}\cdot B_i \right\}$$

这是一个斜率优化的经典形式，设：

$$\begin{aligned} x_i &= -A_{i+1}\\ y_i &= f_i\\ k_i &= B_i\\ b_i &= f_i \end{aligned}$$

代入方程，对于任意一个决策 $(x_j, y_j)$，有：

$$b_i = y_j - k_i\cdot x_j$$

对于上式，显然应最小化截距 $b_i$ 的值，可以使用与上面类似的代数推导法证明最优决策点一定位于下凸包上。又 $x_j$、$k_i$ 均随 $i$ 的增加不降，按照例题的套路用单调队列维护下凸包即可。
总时间复杂度 $O(n\log n)$，瓶颈是排序。

代码详见：「笔记」斜率优化 DP。

「SDOI2016」征途

斜率优化 DP，$k_i$、$x_i$ 均单调，单调队列。

王 道 征 途
「そうですね…やっぱり僕は、王道を征く、ソープ系ですか」

给定一列有序的 $n$ 个物品，第 $i$ 个物品的价值为 $a_i$。
给定参数 $m$，要求将一列物品分成 $m$ 段，最小化每段长度之和的方差 $v$，输出 $v\cdot m^2$。
$1\le n\le m\le 3000$，$\left(\sum a_i\right)\le 3\times 10^4$。
1S，256MB。

记划分出的 $m$ 段的和分别为 $b_1\sim b_m$，将 $v\cdot m^2$ 展开一下：

$$\begin{aligned} v\cdot m^2 =& m^2\cdot \dfrac{\sum\limits_{i=1}^{m}\left(b_i - \overline{b}\right)^2}{m}\\ =& m\sum_{i=1}^{m} \left( b_i^2 - 2b_i\overline{b} + \overline{b}^2 \right)\\ =& m\sum_{i=1}^{m} \left( b_i^2 - 2b_i\dfrac{\sum_{i=1}^m b_i}{m} + \dfrac{\left(\sum_{i=1}^m b_i\right)^2}{m^2} \right)\\ =& m\sum_{i=1}^{m} b_i^2 - 2\left(\sum_{i=1}^m{b_i}\right)^2 + \left(\sum_{i=1}^m{b_i}\right)\\ =& m\sum_{i=1}^{m} b_i^2 - \left(\sum_{i=1}^{m}{b_i}\right)^2 \end{aligned}$$

发现最后的式子中 $\left(\sum{b_i}\right)^2$ 等于 $\left(\sum{a_i}\right)^2$，是一个定值，仅需最小化第一项即可。

按传统先写个暴力，设 $f_{i,j}$ 表示将前 $i$ 个数划分为 $j$ 段时 $\sum b_i^2$ 的最小值，转移时枚举段数 $k$ 和上一段的结尾 $j$，则有：

$$f_{i,k} = \min_{j=0}^{i-1} \left\{ f_{j,k-1} + \left(\sum_{l=j+1}^{i}a_l\right)^2\right\}$$

预处理前缀和后暴力转移复杂度 $O(n^2m)$，考虑优化。
发现后一项是一个区间和的平方的形式，它同时与 $i,j$ 有关。考虑对 $a$ 做一个前缀和，设 $s_i = \sum_{i=1}^{i} a_i$，将其代入原式：

$$\begin{aligned} f_{i,k} &= \min_{j=0}^{i-1} \left\{ f_{j,k-1} + \left( s_i - s_j \right)^2 \right\}\\ f_{i,k} &= \min_{j=0}^{i-1} \left\{ f_{j,k-1} + s_i^2 - 2s_is_j +s_j^2 \right\} \end{aligned}$$

考虑先通过枚举固定 $k$，对于每一个决策 $f_{j,k}$，都有：

$$f_{i,k} - s_{j}^2= \left(f_{j,k - 1} + s_j^2\right) - 2s_is_j$$

这是一个显然的斜率优化的形式，套路地设：

$$\begin{aligned} x_i &= s_i\\ y_i &= f_{i,k-1} + s_i^2\\ k_i &= 2s_i\\ b_i &= f_{i,k} - s_i^2 \end{aligned}$$

对于上式，显然应最小化截距 $b_i$ 的值，易证最优决策点一定位于下凸包上。又 $x_j$、$k_i$ 均随 $i$ 的增加而增加，单调队列维护下凸包即可。注意一些初始化的小问题，详见代码。
总复杂度 $O(nm)$ 级别。

代码详见：「笔记」斜率优化 DP。

CF311B Cats Transport

斜率优化 DP，$k_i$、$x_i$ 均单调，单调队列。

一条数轴上有 $n$ 个点，第 $i$ 个点与第 $i-1$ 个点的距离为 $d_i$，有 $p$ 个人在第 $1$ 个点上。有 $m$ 只 neko，第 $i$ 只 neko 位于第 $h_i$ 个点上，neko 会在 $T_i$ 时间开始等待人的到来。
没个人可以从任意时间从第 $1$ 个点出发，按编号顺序依次经过各点，速度为 1 个单位长度 1 秒，中间不停下。每经过一个点，就会将该点上处于等待状态的 neko 接上。
每只 neko 的等待时间为其被接上时间与开始等待时间的差。要求安排每个人出发的时间，最小化 neko 等待的时间之和。
$2\le h_i\le n\le 10^5$，$1\le m\le 10^5$，$1\le p\le 100$，$1\le d_i\le 10^4$，$1\le T_i\le 10^9$。
2S，256MB。

可以简单地 YY 出一个与 $t$ 相关的 DP 状态，但 $t$ 过大，猜测 DP 状态与 $t$ 无关，考虑找下结论。可以发现每个人接上的 neko 中，至少有一只恰好刚开始等待人的到来。正确性显然，若所有 neko 都是等待了一段时间后再被接上，不如提前人的出发时间，直到有一只刚开始等待，在不影响接上了哪些 neko 的前提下减少等待时间之和。

前缀和预处理点 $1$ 到各点的距离 $\operatorname{dis}_i$。对于每只 neko，容易求得一个人从何时出发能够恰好接上它，显然该时间为 $t_i = T_i - \operatorname{dis}_{h_i}$。
考虑将所有 neko 按照 $t_i$ 排序。显然在满足一开始的结论的前提下，每个人接到的 neko 都对应排序后的一段区间 $[l,r]$，刚开始等的 neko 一定是第 $r$ 只 neko（即 $t_i$ 最大的），则这个人的出发时间为 $t_r$，区间内 neko 的等待时间之和为 $\sum t_r - t_i$。
问题可以抽象为给定一长度为 $m$ 的数列 $t$，要求将 $t$ 分为 $p$ 段，每段的代价为该段最右的数减去该段每个值的和，最小化代价和。

对于抽象后的问题，设 $s_i = \sum_{j\le i}t_j$，设 $f_{i,j}$ 表示将前 $i$ 个数分为 $j$ 段的最小代价和，转移时先枚举段数 $k$，再枚举最后一段，则有：

$$\begin{aligned} f_{i,k} &= \min_{j = 0}^{i - 1} \left\{ f_{j, k - 1} + \sum_{l = j + 1}^{i} \left( t_i - t_l \right) \right\}\\ &= \min_{j = 0}^{i - 1} \left\{ f_{j, k - 1} + (i - j)t_i - (s_i - s_j) \right\}\\ &= i\cdot t_i -s_i + \min_{j = 0}^{i - 1} \left\{ \left(f_{j, k - 1} +s_j\right) - t_i\cdot j \right\} \end{aligned}$$

方程中出现了乘积项，先通过枚举固定 $k$ 后，这显然是一个可以斜率优化的形式，套路地设：

$$\begin{aligned} x_i &= i\\ y_i &= f_{i,k - 1} + s_j\\ k_i &= t_i\\ b_i &= f_{i,k} - i\cdot t_i + s_i \end{aligned}$$

显然应最小化 $b_i$，又 $x_i$ 与 $k_i$ 都随 $i$ 的增加单调不降，单调队列维护下凸包即可。
总复杂度 $O(n + m\log m + pm)$ 级别。

代码详见：「笔记」斜率优化 DP。

P2365 任务安排

斜率优化 DP，$k_i$、$x_i$ 均单调，单调队列。

三 步 走 战 略

给定一列 $n$ 个有序的物品，每个物品有两个属性 $(t_i, g_i)$，给定参数 $s$。
要求将物品分为任意段，第 $i$ 段 $[l_i,r_i]$ 的代价为 $\left(is + \sum_{j=l_i}^{r_i} t_j\right)\cdot \sum_{k=l_i}^{r_i}$，要求最小化分段的代价之和。
$1\le n\le 5000$，$0\le s\le 50$，$1\le t_i,g_i\le 100$。
1S，128MB。

发现分到第几段对答案有影响，设 $f_{i,j}$ 表示将前 $i$ 个任务分为 $j$ 段的最小费用和，转移时枚举段数 $k$ 和最后一段，则有：

$$f_{i,k} = \min_{j=0}^{i - 1} \left\{ f_{j,k-1} + \left(ks + \sum_{k=j+1}^{i} t_k \right)\sum_{l=j + 1}^{i} g_l \right\}$$

预处理前缀和，暴力转移时间复杂度 $O(n^3)$，空间复杂度 $O(n^2)$。空间和时间都菜爆了。

---

发现在上述算法中必须枚举分到第几段，考虑能否优化掉状态的这一维，并优化转移。
这里用到了一种叫做「费用提前计算」的思想。发现每次转移将 $[j + 1,i]$ 这段分出后，后续元素的代价里都会加上 $k\cdot g$，考虑在状态转移中加上这部分的影响。具体地，将状态删去一维，方程改写为如下所示：

$$f_i = \min_{j=0}^{i-1}\left\{ f_j + \sum_{k=1}^{i} t_k\sum_{l=j + 1}^{i} g_l + s\left( \sum_{k = j + 1}^{n} g_k\right)\right\}$$

状态转移方程很容易理解。此时已经无法准确定义 $f$ 的含义了，但 $f_n$ 一定表示将所有物品划分为某几段的最小代价和，且这样转移一定可以保证 $f_n$ 的正确性。

预处理前缀和后暴力转移即可，时间复杂度 $O(n^2)$，空间复杂度 $O(n)$。

---

上述 $O(n^2)$ 算法已经可以通过原题了，但这还不够。

记 $st_x = \sum_{i=1}^{x} t_i$，$sg_x = \sum_{i=1}^x g_i$，代入转移方程并略作变换：

$$\begin{aligned} f_i &= \min_{j=0}^{i-1}\left\{ f_j + st_i\left( sg_i - sg_j \right) + s\left( sg_n - sg_j\right)\right\}\\ f_i - st_i\cdot sg_i - s\cdot sg_n&= \min_{j=0}^{i-1} \left\{ \left(f_j - s\cdot sg_j \right) - st_i\cdot sg_j \right\} \end{aligned}$$

这是一个显然的斜率优化的形式，设：

$$\begin{aligned} x_i &= sg_i\\ y_i &= f_ i- s\cdot sg_i\\ k_i &= st_i\\ b_i &= f_i - st_i\cdot sg_i - s\cdot sg_n \end{aligned}$$

由于 $0\le t_i,g_i$，$k_i$ 与 $x_i$ 均单调递增，套路地单调队列维护下凸包即可。
总时空复杂度均为 $O(n)$。

代码详见：「笔记」斜率优化 DP。

「SDOI2012」任务安排 3

斜率优化 DP，$x_i$ 单调，$k_i$ 不单调，单调栈，二分。

与上题仅有数据范围不同

给定一列 $n$ 个有序的物品，每个物品有两个属性 $(t_i, g_i)$，给定参数 $s$。
要求将物品分为任意段，第 $i$ 段 $[l_i,r_i]$ 的代价为 $\left(is + \sum_{j=l_i}^{r_i} t_j\right)\cdot \sum_{k=l_i}^{r_i}$，要求最小化分段的代价之和。
$1\le n\le 3\times 10^5$，$1\le s\le 2^8$，$|t_i|\le 2^8$，$0\le g_i\le 2^8$。
1S，512MB。

考虑上题最后得到的斜率优化的式子。与上题不同的是，本题中可能出现 $t_i< 0$，$k_i$ 是不单调的，这影响了最优决策点的选择，无法使用单调队列选择最优决策点。但 $x_i$ 单调，使用单调队列维护下凸包的做法是正确的。

仍考虑使用单调队列维护下凸包，每次查询最优决策点时在凸包上二分，找到第一个使得左侧斜率小于 $k_i$，右侧斜率不小于 $k_i$ 的位置即为最优决策点，不从队首弹出元素。可以发现此时的“单调队列”实际上是一个单调栈。我们实际上是在用 Andrew 算法 维护凸包。

总时间复杂度变为 $O(n\log n)$。

代码详见：「笔记」斜率优化 DP。

「APIO2018」铁人两项

圆方树，树形 DP。

给定一 $n$ 个节点 $m$ 条边的无向图，求存在多少对有序三元组 $(s,c,f)$，满足 $s,c,f$ 互不相同且存在一条从 $s$ 到 $f$ 的简单路径使得 $c$ 在路径上出现。
$1\le n\le 10^5$，$1\le m\le 2\times 10^5$。
1S，1G。

利用一个点双的性质，对于点数 $\ge 3$ 的点双中任意两个不同的点之间，一定存在一条简单路径经过在同一点双内的任意一点。证明详见 OI-Wiki 圆方树页面。

于是可以考虑建出原图的圆方树。考虑圆方树上任意两个圆点 $x,y$ 之间的路径上的点：对于路径上某圆点 $z$，显然原图中 $z$ 一定在 $x$ 到 $y$ 的一条简单路径上，三元组 $(x,z,y)$ 对答案有贡献。对于路径上某方点，根据上述性质，方点所对应的点双中的所有节点也一定可以出现在 $x$ 到 $y$ 的一条简单路径上。
则对于圆方树上任意两圆点 $s,f$，能与它们组成合法有序三元组的 $c$ 即为圆方树上两点路径上圆点与方点维护的所有圆点并集的大小减 2（不包含 $s,f$）。考虑到圆方树上圆点只与方点相连，方点只与圆点相连，路径上的圆点一定被路径上它们相邻的方点维护，考虑给各点赋值来方便统计。

考虑令方点权值变为代表的点双的大小，圆点的权值为 $-1$。圆方树上任意两圆点对答案的贡献即为路径上点权之和。问题变为统计树上所有以圆点为端点路径权值之和。转化为每个点被多少路径所包括，简单树形 DP 即可。总时间复杂度 $O(n)$ 级别。

注意原图可能不连通。

代码中并没有显式的 DP 数组。

代码详见：「APIO2018」铁人两项 - Luckyblock。

P4719 【模板】"动态 DP"&动态树分治

树形 DP，矩阵乘法，重链剖分，线段树

宣传一波：「笔记」广义矩阵乘法与 DP。

给定一棵 $n$ 个点的树，点有点权。给定 $m$ 次点权修改操作，求每次操作后整棵树的 最大点权独立集 的权值。
一棵树的独立集定义为满足任意一条边的两端点都不同时存在于集合中的树的一个点集，一个独立集的价值定义为集合中所有点的点权之和。
$1\le n,m\le 10^5$，$-100\le$ 点权 $\le 100$。
1S，256MB。

以下是前置知识，简单介绍广义矩阵乘法。

对于一 $p\times m$ 的矩阵 $A$，与 $m\times q$ 的矩阵 $B$，定义广义矩阵乘法 $A\times B = C$ 的结果是一个 $p\times q$ 的矩阵 $C$，满足：

$$C_{i,j} = (A_{i, 1}\otimes B_{1,j}) \oplus (A_{i,2}\otimes B_{2,j})\oplus \cdots \oplus (A_{i, n}\otimes B_{n,j})$$

其中 $\oplus$ 与 $\otimes$ 是两种二元运算。

考察这种广义矩阵乘法是否满足结合律：

$$\begin{aligned} ((AB)C)_{i,j} &= \bigoplus_{k=1}^{p}(AB)_{i,k}\otimes C_{k,j}\\ &= \bigoplus_{k=1}^{p}\left( \left(\bigoplus_{t=1}^{q} A_{i,t}\otimes B_{t,k}\right) \otimes C_{k,j}\right)\\ (A(BC))_{i,j} &= \bigoplus_{t=1}^{q}A_{i,t}\otimes (BC)_{t,j}\\ &= \bigoplus_{t=1}^{q} \left(A_{i,t}\otimes \left(\bigoplus_{k=1}^{p} B_{t,k} \otimes C_{k,j}\right)\right) \end{aligned}$$

显然，若 $\otimes$ 运算满足交换律、结合律，且 $\otimes$ 对 $\oplus$ 存在分配律，即存在 $\left(\bigoplus a\right)\otimes b = \bigoplus \left( a\otimes b \right)$ 时，广义矩阵乘法满足结合律。根据上述运算规律，对二式进行 $\oplus$ 的交换后有：

$$((AB)C)_{i,j} = (A(BC))_{i,j} = \bigoplus_{k=1}^{p}\bigoplus_{t=1}^{q} \left(A_{i,t}\otimes B_{t,k}\otimes C_{k,j}\right)$$

---

回到此题，先考虑朴素 DP。钦定 1 为根，设 $f_{u,0/1}$ 表示钦定点 $u$ 不在/在 独立集时以 $u$ 为根的子树的最大点权独立集的权值，显然有：

$$\begin{aligned} f_{u,0} &= \sum_{v\in \mathbf{son}(u)} \max(f_{v, 0}, f_{v,1})\\ f_{u,1} &= \operatorname{val}_u + \sum_{v\in \operatorname{son}(u)} f_{v, 0} \end{aligned}$$

答案即为 $\max (f_{1,0}, f_{1, 1})$。

要求支持修改，又树的形态不变，考虑用树链剖分维护。但发现每个节点的 DP 值与其所有儿子有关，而树剖只能支持修改重链/子树信息。于是考虑对于每个节点，先将其轻儿子的贡献求和，再考虑其重儿子的贡献，使得可以通过对重链的修改/查询来维护上述信息。这种思想在 LCT 维护子树信息时也有所应用。
记 $g_{u,0/1}$ 表示钦定 $u$ 的重儿子不在独立集，点 $u$ 不在/在 独立集时以 $u$ 为根的子树的最大点权独立集的权值。记 $\operatorname{s}_u$ 表示 $u$ 的重儿子，显然有：

$$\begin{aligned} g_{u,0} &= \sum_{v\in \operatorname{son}(u) \land v\not= \operatorname{s}_u}\max(f_{v,0}, f_{v,1})\\ g_{u,1} &= \operatorname{val}_u + \sum_{v\in \operatorname{son}(u) \land v\not = \operatorname{s}_u} f_{v, 0} \end{aligned}$$

则对 $f$ 的转移可以改写成下列形式：

$$\begin{aligned} f_{u,0} &= g_{u,0} + \max(f_{\operatorname{s}_u, 0}, f_{\operatorname{s}_u,1})\\ f_{u,1} &= g_{u,1} + f_{\operatorname{s}_u, 0} \end{aligned}$$

考虑加法运算运算与取 $\max$ 运算的性质：发现取 $\max$ 满足交换律与结合律，且加法对取 $\max$ 满足分配率，即有：

$$a + \max_{i}(b_i) = \max_{i}(a + b_i)$$

考虑定义一种广义矩阵乘法 $A\times B = C$，满足：

$$C_{i,j} = \max_{k}\left( A_{i,k} +B_{k,j}\right)$$

根据上述转移方程，有下列关系成立。

$$\large \begin{bmatrix} g_{u,0}& g_{u,0}\\ g_{u,1}& -\infin \end{bmatrix} \times \begin{bmatrix} f_{\operatorname{s}_u, 0}\\ f_{\operatorname{s}_u, 1} \end{bmatrix} = \begin{bmatrix} f_{u, 0}\\ f_{u, 1} \end{bmatrix}$$

于是可以考虑先预处理出 $g$ 数组初始化转移矩阵，再使用线段树维护区间矩阵乘积。转移矩阵写在前面是因为 dfs 序列中深度较浅的点在前，转移矩阵写在前面可以直接按 dfs 序求得区间矩阵乘积并转移。若转移矩阵写在后面，需要先将区间内的元素顺序反转。经过预处理后，求得以 1 为根的重链对应区间的矩阵乘积，即得 $f_{u,0}$ 与 $f_{u,1}$。正确性显然，重链一定以某叶节点为链底，以 1 为根的重链上所有轻儿子子树信息的并即为整棵树的信息。

考虑修改操作对哪些位置的 $g$ 会产生影响。考虑其实际含义，$g$ 维护的是轻儿子子树信息。被影响的节点显然为指定的修改位置 $x$，以及子树中包含被修改位置，且为轻儿子的节点的父亲，后者可以通过从被修改位置不断跳重链来进行遍历。每次跳到的重链的顶的父亲，即为对应节点。
每次更新上述节点时先求得修改前以该节点的对应轻儿子的子树信息，修改子树中的节点后再求得该节点的对应轻儿子子树信息。根据两次求得的子树信息的差更新该节点的 $g$，并将即将被修改的节点调整为当前节点。建议结合代码理解。

总复杂度 $O(8n\log n + 8m\log^2 n)$ 级别。

代码详见：P4719 【模板】动态 DP&动态树分治 - Luckyblock。

P3403 跳楼机

DP，最短路。

最短路算法本质上还是一种 DP。这里是借用了最短路来优化 DP。

给定参数 $h, x, y, z$，求 $[1, h]$ 中有多少数 $i$ 能被表示成 $i = (k_1\times x + k_2\times y + k_3\times z + 1)\ (k_1, k_2, k_3\in \N)$ 的形式。
$1\le h\le 2^{63} - 1$，$1\le x, y, z\le 10^5$。
1S，128MB。

只能说这种做法太妙了……实在是不知道怎么梳理出一个合理的思路，直接写做法了。

首先令 $h-1$，求 $[0, h-1]$ 中有多少数 $i$ 能被表示成 $i = k_1\times x + k_2\times y + k_3\times z\ (k_1, k_2, k_3\in \N)$ 的形式。

我们在 $\bmod x$ 意义下考虑使用 $y, z$ 能组合出的数，记 $f_{i}$ 为满足 $f_{i} \bmod x = i$ 的最小的数。显然对于大于 $f_i$ 且满足 $j\bmod x = i$ 的所有数 $j$，都可以通过在 $f_{i}$ 基础上加数个 $x$ 凑出来，而小于 $f_i$ 且满足 $j\bmod x = i$ 的所有数 $j$ 均是无法被凑出来的，这些合法的数的数量为：$\left\lfloor \frac{h- f_i}{x} \right\rfloor + 1$。

问题变为如何快速处理出 $f_i$。考虑 DP。初始化 $f_{0} = 0$，则可以写出一个粗陋的式子：

$$f_i = \min_{(j + y) \equiv i \lor (k + z) \equiv i \pmod x}\{ f_{j} + y, f_k + z\}$$

发现由于枚举顺序难以确定，这个转移是没法直接做的。但它的形式和性质和求最短路是一致的，于是考虑建图转化成求最短路。建立一张 $x$ 个节点的有向带权图，从节点 0 到节点 $i(0\le i\le n - 1)$ 的最短路即为 $f_i$。建图时枚举 $u\in [0, n - 1]$，从 $u$ 向 $(u + y)\bmod x$ 连一条权值为 $y$ 的有向边，向 $(u + z)\bmod x$ 连一条权值为 $z$ 的有向边。跑出来最短路即可计算答案。

总时间复杂度 $O(x\log x)$ 级别。

代码详见：P3403 跳楼机 - Luckyblock。

CF1792E

数论，子集 DP。

$t$ 组数据，每组数据给定参数 $n, m_1, m_2$。对于 $m_1\times m_2$ 的约数 $d$，记满足 $\exist 1\le x, y\le n, d = x\times y$ 的最小的 $x$ 为 $x_d$，求上述 $x_d$ 的个数，并输出所有 $x_d$ 的异或和。
$1\le t\le 10$，$1\le n, m_1, m_2\le 10^9$。
2.5S，256MB。

写了个 $O(m)$ 的质因数分解我是超级大啥b。

前置知识：约数个数的上界估计：https://www.cnblogs.com/ubospica/p/10392523.htm、https://blog.csdn.net/VFleaKing/article/details/88809335。
省流版：$10^{18}$ 内的数约数至多有 $103680\approx 10^5$ 个。

于是考虑先对 $m_1, m_2$ 进行质因数分解，再暴力凑出 $m_1\times m_2$ 的所有约数，问题变为对每一个约数 $d$ 求得一组满足上述条件的 $(x,y)$，且满足 $x$ 尽可能地小，则 $y$ 应当是满足 $y\le n$ 的最大的 $d$ 的约数。如果我们可以求得每个约数 $d$ 对应的 $y$，那么只需检测 $x = \frac{d}{y} \le n$ 是否成立即可判断 $d$ 是否对答案有贡献。

直接暴力枚举 $y$ 的复杂度是无法承受的。考虑子集 DP。记 $f_{d}$ 表示满足 $y\le n$ 的 $d$ 的最大的约数。对于 $d\le n$，显然有 $f_{d} = d$；对于 $d>n$，考虑枚举 $d$ 的质因子 $p$，有：

$$f_{d} = \max_{p|d} f_{\frac{d}{p}}$$

$m_1\times m_2$ 的质因子的数量级只有 $10$ 左右，DP 复杂度并不高。处理出 DP 值后累计有贡献的 $f_{d}$ 即可。总复杂度约为 $O(t(\sqrt{m_1 + m_2} + 10 \times \operatorname{d}(m_1\times m_2)))$ 级别。

DP 时要注意实现，虽然出题人没卡，但直接用 map 让 $d$ 作 $f$ 的下标跑的相当慢。应当令 $d$ 的编号作 $f$ 的下标，转移时使用二分查找 $f_{\frac{d}{p}}$ 即可。

代码详见：Educational Codeforces Round 142 - Luckyblock。

「NOIP2012」开车旅行

模拟，倍增

懒得简述的题面。

先考虑暴力模拟。先预处理出从每个城市出发，A/B 开车到达的下一个城市。预处理时可以考虑倒序枚举所有城市，维护一棵以海拔为权值的平衡树，将当前枚举的城市插入平衡树，查询前驱、前驱的前驱、后继、后继的后继，在这四个城市中找距离的最小值和次小值即可。注意先插入两个极小值和两个极大值。之后对于第一、二问，模拟每天的行程直至无法前进即可。

这样每次查询的复杂度是 $O(n)$ 的，考虑优化，倍增预处理从每个城市出发，A/B 先开车，经过 $2^i$ 天的行程信息。具体地，设：$f_{i,j,0/1}$ 表示 A/B 先开车，从城市 $j$ 出发，经过 $2^i$ 天后到达的城市，$\operatorname{disa}_{i,j,0/1}$、$\operatorname{disb}_{i,j,0/1}$ 表示表示 A/B 先开车，从城市 $j$ 出发，经过 $2^i$ 天后 A/B 的行程。首先根据暴力中预处理的信息初始化 $f_{0,i,0/1}, \operatorname{disa}_{0,i,0/1}, \operatorname{disb}_{0,i,0/1}$，然后进行倍增，有：

• 当 $i=1$ 时，前半段和后半段路程开车人不同。设前半段开车人为 $k$，则有：

  $$\begin{aligned} f_{1, j, k} &= f_{0, (f_{0, j, k}), 1-k}\\ \operatorname{disa}_{1, j, k} &= \operatorname{disa}_{0, j, k} + \operatorname{disa}_{0, (f_{0, j, k}), 1-k} \\ \operatorname{disb}_{1, j, k} &= \operatorname{disb}_{0, j, k} + \operatorname{disb}_{0, (f_{0, j, k}), 1-k} \end{aligned}$$

• 当 $i>1$ 时，有：

  $$\begin{aligned} f_{i, j, k} &= f_{i - 1, (f_{i - 1, j, k}), k}\\ \operatorname{disa}_{i, j, k} &= \operatorname{disa}_{i - 1, j, k} + \operatorname{disa}_{i - 1, (f_{i - 1, j, k}), k} \\ \operatorname{disb}_{i, j, k} &= \operatorname{disb}_{i - 1, j, k} + \operatorname{disb}_{i - 1, (f_{i - 1, j, k}), k} \end{aligned}$$

利用倍增预处理的信息加速模拟的过程即可，总复杂度 $O((n + m)\log n)$ 级别。

set 的迭代器只能进行 ++/-- 操作，注意从 set 中取前驱后继的写法。

代码详见：「NOIP2012」开车旅行 - Luckyblock。

P4766 [CERC2014]Outer space invaders

区间 DP

有 $n$ 匹黄金船赶来侵略地球。第 $i$ 匹黄金船会在时间 $a_i$ 出现在距离你 $d_i$ 的位置，被消灭的时间不能大于 $b_i$，否则你就会被外星怪马抓回她的母星每天做十万次马儿跳。在任一时刻你可以释放一次距离为 $R$ 的忍术，花费 $R$ 的代价将距离你不大于 $R$ 的黄金船干掉。求不被抓走前提下干掉所有黄金船的最小代价。
$T$ 组数据，每组数据给定长度为 $n$ 的三个数列 $a,b,d$，描述了一次外星怪马的侵略，求抵挡这次侵略的最小代价。
$1\le n\le 300$，$1\le a_i<b_i\le 10^4$，$1\le d_i\le 10^4$。
题面中没有给出 $T$ 的范围，但经测试 $T$ 并不影响总复杂度。
2S，128MB。

假算法一

我想到一个线性 DP！

显然只在恰好 $b_i$ 时刻释放忍术是最优的。考虑先将黄金船按 $b_i$ 升序排序，这样在后面的忍术对是否消灭了前面的黄金船没有影响。设 $f_i$ 表示消灭前 $i$ 匹黄金船的最小代价，转移时枚举最后一次释放忍术的时刻 $b_j$，考虑最后一次释放忍术把 $j\sim i$ 这一段黄金船全部消灭，则在满足 $\left( \max_{k=j}^{i} a_i \le b_j\right)$ 条件下，有：

$$f_i = \min_{j= 1}^{i}\left( f_{j - 1}+ \max_{k = j}^{i} d_k\right)$$

答案即 $f_n$，总复杂度 $O(n)$ 级别。

然而假了。虽然排序后后面的忍术不会影响前面的黄金船，但前面的忍术会影响到后面的黄金船。具有后效性，无法进行线性 DP。

---

真算法一

发现 $n$ 较小，但 $a,b$ 较大，考虑先离散化，记离散化后最大的时刻为 $m$。

按时间顺序枚举具有后效性，则考虑对时间维进行区间 DP。设 $f_{i,j}$ 表示将满足 $i\le a_p < b_p\le j$ 的黄金船 $p$ 全部消灭的代价。转移时考虑最后在位置 $k(i\le k\le j)$ 进行的一次操作，在这次操作之前消灭了 $[a_p,b_p]\subseteq [i,k-1]$ 和 $[a_p, b_p]\subseteq [k+1,i]$ 中的所有黄金船 $p$，这次操作消灭了满足 $i\le a_p \le k \le b_p\le j$ 的全部黄金船，即有：

$$f_{i,j} = \min_{k=i}^{j}\left( f_{i, k - 1} + f_{k + 1, j} + d_{i,j,k}\right)$$

上式中 $d_{i,j,k}$ 表示满足：$i\le a_p \le k \le b_p\le j$ 的黄金船 $p$ 中最远的距离，即：

$$d_{i,j,k} = \max_{i\le a_p \le k \le b_p\le j} d_p$$

最终答案即 $f_{1,m}$。

发现 DP 的过程是 $O(n^3)$ 级别的，但预处理 $d$ 是 $O(n^4)$ 级别的，不预处理则 DP 变为 $O(n^4)$ 级别，无法通过本题。

---

真算法二

发现复杂度瓶颈出在取最大值的过程中。取最大值的目的是得到 $[a_p, b_p]$ 跨越区间分界点 $k$ 的最大的 $d_p$，计算出使得 $[i,j]$ 中的黄金船全部被消灭的最后一次操作的代价。

发现操作的顺序并不影响正确性，我们不妨钦定满足 $[a_p,b_p]\subseteq [i,j]$ 的 $d_p$ 最大的黄金船是在最后一次操作中被消灭的。转移时先求得这匹黄金船的编号 $\operatorname{id}$，则枚举的分界点 $k$ 被限定在了 $[a_{\operatorname{id}}, b_{\operatorname{id}}]$ 中，有：

$$f_{i,j} = \min_{k=a_{\operatorname{id}}}^{b_{\operatorname{id}}}\left( f_{i, k - 1} + f_{k + 1, j} + d_{\operatorname{id}}\right)$$

仅需在枚举 $k$ 之前 $O(n)$ 地求得 $\operatorname{id}$ 即可。答案仍为 $f_{1,m}$。总复杂度 $O(n^3)$ 级别，可以通过本题。

---

真算法三

真算法二和其他题解中的写法已经非常类似了，但其他题解中在转移时没有分界点 $k$ 的限制，为什么仍然得到了正确的答案呢？换言之，怎么保证 $k\notin [a_{\operatorname{id}}, b_{\operatorname{id}}]$ 的转移一定不优于 $k\in [a_{\operatorname{id}}, b_{\operatorname{id}}]$ 的转移呢？

需要指出的是，真算法二实际上是对真算法一的一种减去无用转移的优化。我们考虑一次 $k\notin [a_{\operatorname{id}}, b_{\operatorname{id}}]$ 的转移 $f_{i,j} = \min\left( f_{i, k - 1} + f_{k + 1, j} + d_{\operatorname{id}}\right)$。此时有 $[a_{\operatorname{id}}, b_{\operatorname{id}}] \subseteq [i,k-1]$ 或 $[a_{\operatorname{id}}, b_{\operatorname{id}}]\subseteq [k+1, j]$，若这里的 $f_{i,j}$ 定义不变，则最大的代价 $d_{\operatorname{id}}$ 已经在 $f_{i,k-1}$ 或 $f_{k+1,j}$ 中被计算了一次了。更进一步地，在真算法一中，我们在计算 $f_{i,j}$ 时选择的是 $k\in [a_p, b_p]$ 的最大的代价 $d_p$，显然有 $d_p\le d_{\operatorname{id}}$。当我们在真算法二中进行 $k\in [a_{\operatorname{id}}, b_{\operatorname{id}}]$ 的转移时，$d_p$ 的贡献也是已经被包含在了 $f_{i,k-1}$ 或 $f_{k+1,j}$ 中了。

总结一下，$k\notin [a_{\operatorname{id}}, b_{\operatorname{id}}]$ 的转移实质上都是 $k\in [a_{\operatorname{id}}, b_{\operatorname{id}}]$ 的转移重复状态，把它们都考虑上也并不会影响正确性。

代码详见：P4766 [CERC2014]Outer space invaders - Luckyblock。

学到了什么

枚举边界

考虑实际意义，对枚举的边界进行修改，减少枚举的复杂度。

P5017 摆渡车

无用决策

删去无用的决策，包括不合法，较劣等情况。

P5017 摆渡车

P2943 [USACO09MAR]Cleaning Up G - Luckyblock

预处理

可通过预处理转移时的某些常量（某些区间的贡献、逆元等），来减小转移复杂度。

P5017 摆渡车

「NOI2015」寿司晚宴

CF1437F Emotional Fishermen

相对大小

转移时只受相对大小的影响，可考虑记录差值。

P4933 大师

P5664 Emiya 家今天的饭

决策单调性

观察单调性，减去无用状态。（单调队列、栈优化）。

P5858 「SWTR-03」Golden Sword

P1973 [NOI2011]NOI 嘉年华

P3287 [SCOI2014]方伯伯的玉米田

可枚举性

如果数据范围较小或 有特殊性质，可考虑直接暴力枚举相关元素进行转移。

P5664 Emiya 家今天的饭

P1973 [NOI2011]NOI 嘉年华

P2051 [AHOI2009]中国象棋

P2943 [USACO09MAR]Cleaning Up G - Luckyblock

「AHOI2009」同类分布

二叉树转移时可直接枚举左右儿子。

P1270 “访问”美术馆

排序问题

对一类排序问题可先考虑两个元素的关系，再进行推广。

P2577 [ZJOI2005]午餐

补集转化

注意补集转换。

P2577 [ZJOI2005]午餐

P2501 [HAOI2006]数字序列

CF1437E Make It Increasing

贡献合并

考虑同类元素贡献合并。

P4158 [SCOI2009]粉刷匠

如果 价值与代价 为同一类型，且可以合并，则可以合并，以减小分析以及代码的复杂度。

P1846 游戏

区间查询

不满足单调性，可考虑线段树维护，实现修改与查询。

P1295 [TJOI2011]书架

差分

区间修改考虑差分。

CF79D Password

倒序枚举

防止重复更新，可考虑倒序枚举。

P1273 有线电视网

P3287 [SCOI2014]方伯伯的玉米田

出现前面的操作影响后面的贡献的情况。

[「CSP-S 2020」函数调用]

数据结构直接维护

形式优美时，可直接用数据结构来维护 DP 数组。

P3287 [SCOI2014]方伯伯的玉米田

确定元素是否位于方案中

对于一类最优化方案计数问题，比如 LIS，最短路等，要求一个元素是否存在于最优方案中。
可以考虑求得该元素前后两侧的贡献，贡献合并后判断是否等于最优方案的贡献。
判断一个数是否位于 LIS 中，可以判断以该数结尾 + 以该数开始 的LIS长度之和 - 1，是否等于总 LIS。
判断一个点是否在最短路中，可以判断从 S 到该点的距离 + 从终点到该点的距离，是否等于最短路长度。

P2487 [SDOI2011]拦截导弹

拓扑序应用

对于一类计数类树形 DP

如果贡献是比较复杂的式子，可先将式子拆分，统计时考虑增量法。
即考虑单个子树，与已经统计的子树信息组合产生的影响。

P1351 联合权值

换根 DP

需要同时维护子树和祖先的信息，考虑换根 DP。
钦定 1 为根，第一次 dfs 处理子树信息，第二次 dfs 处理祖先信息进行换根。
在第二次 dfs 时一般需要下传维护的祖先信息。

P3478 [POI2008]STA-Station

CF708C Centroids

分段 DP

分成多段进行 DP，再对 DP 数组进行合并。
减小空间复杂度。

「NOI2015」寿司晚宴

或者有多段互相独立的情况，分段 DP 贡献直接累加即可。

CF1437E Make It Increasing

AC 自动机上 DP

给定一些字符串的限制，询问满足条件的字符串的数量时，可以考虑在 AC 自动机上 DP，模拟匹配的过程。
套路地设 $f_{i,j}$ 表示匹配到第 $i$ 位，当前匹配状态为 $j$ 时的贡献。转移时枚举状态对应的转移函数更新即可。
可以滚动数组优化。

「JSOI2007」文本生成器

「SDOI2014」数数

「BJOI2019」奥术神杖

斜率优化

转移方程呈现 $f_i = \operatorname{min}/\operatorname{max}(f_j + g_i \cdot h_j)$ 的形式，即方程中出现乘积项 $g_i\cdot h_j$ 时，可以按照上述套路，将 $f_i$ 看做斜率 $k_i$，将 $h_j$ 看做自变量 $x_j$，$f_j$ 看做函数值 $y_j$。

此时最小/最大化 $f_i$ 的过程与最小/最大化过众多决策点之一的、斜率确定的函数截距的过程一致。可以看做一条斜率为 $k_i$ 的直线自下向上移动，移动过程中第一个出现在直线上的点即为最优的决策。

可以考虑先维护包含最优决策点的凸包，再找到凸包上的最优决策点。当 $k_i, x_i$ 均如例题一样单调时，可使用单调队列维护凸包并找到最优决策点。否则要考虑使用其他手段维护。$k_i$ 不单调会影响最优决策点的位置，$x_i$ 不单调会影响对凸包的维护，详见下方例题部分。

P2900 [USACO08MAR]Land Acquisition G

「SDOI2016」征途

CF311B Cats Transport

P2365 任务安排

「SDOI2012」任务安排 3

圆方树 DP

一些仙人掌/一般无向图上的问题 可以通过建立圆方树高效解决。圆方树上 DP 时一般要考虑一些连通性的结论。

「APIO2018」铁人两项

动态 DP

将转移转化为广义矩阵乘法形式，利用结合律+数据结构进行维护，以支持修改操作。宣传一波：「笔记」广义矩阵乘法与 DP。

P4719 【模板】"动态 DP"&动态树分治

猜结论

大胆猜！

P1973 [NOI2011]NOI 嘉年华

P2501 [HAOI2006]数字序列

P3287 [SCOI2014]方伯伯的玉米田

P1846 游戏

P3558 [POI2013]BAJ-Bytecomputer

CF1457C Bouncing Ball

杂

• 中序遍历 = 拍扁序。 其每一个子序列 都表示 树联通的一部分。
  P1040 加分二叉树

• 如果转移方程可以化成类似这样一类偏序形式：$f_i = 1 + \max_{j=1}^{i} f_j[a_j<a_i][b_j<b_i]$，可考虑 CDQ 分治进行维护。
  P2487 [SDOI2011]拦截导弹

• 有用点集较小，考虑建立虚树，缩链成边，删去无用子树。
  P2495 [SDOI2011]消耗战
  「HEOI2014」大工程 - Luckyblock

• 如果出现自己转移到自己的情况，考虑化下式子。
  P6858 深海少女与胖头鱼

• 费用提前计算，详见下面的博文中 $O(n^2)$ 的解法。
  P2365 任务安排