「笔记」可持久化线段树
写在前面
Q:什么时候需要可持久化?
A:想建一车线段树但是建不下的时候。
引入
给定一长度为 \(n\) 的数列,给定 \(m\) 次操作:
- 在某个历史版本上修改某一个位置上的值。
- 访问某个历史版本上的某一位置的值。
此外,每进行一次操作(对于操作2,即为生成一个完全一样的版本,不作任何改动),就会生成一个新的版本。版本编号即为当前操作的编号(从1开始编号,版本0表示初始状态数组)
\(1\le n,m\le 10^6\),\(0\le |a_i|\le 10^9\)。
1.5S,512MB。
介绍
对于上述问题,朴素的做法是维护 \(m\) 个版本指针。每一次修改后都另外开辟 \(O(n)\) 的空间,将整个数组复制一份,修改后将新版本的指针指向该数组。查询操作则将新版本指针指向被查询的版本。显然上述算法的时空复杂度都是 \(O(nm)\) 的。
但这样太蠢了。可以发现修改操作后新建的数组与原数组其它 \(n-1\) 个位置完全相同,对它们的复制与储存是做负功的。考虑找到一种维护手段,能够重复利用两数组相同的部分,来避免时空的浪费。
考虑把上述操作放到线段树上进行,同样维护 \(m\) 个版本指针,指向每个版本线段树的根。修改时把被操作版本大力复制一份,在新树上单点修改,版本指针更新。查询时直接在被查询版本上查询,并更新版本指针。
可以发现每次单点修改只会访问到自根向下的 \(O(\log n)\) 个节点,在新树中也仅有这 \(O(\log n)\) 个节点的信息与原版本不同。考虑仅新建这 \(O(\log n)\) 个节点,并重复利用原线段树中其它节点,如下图所示:
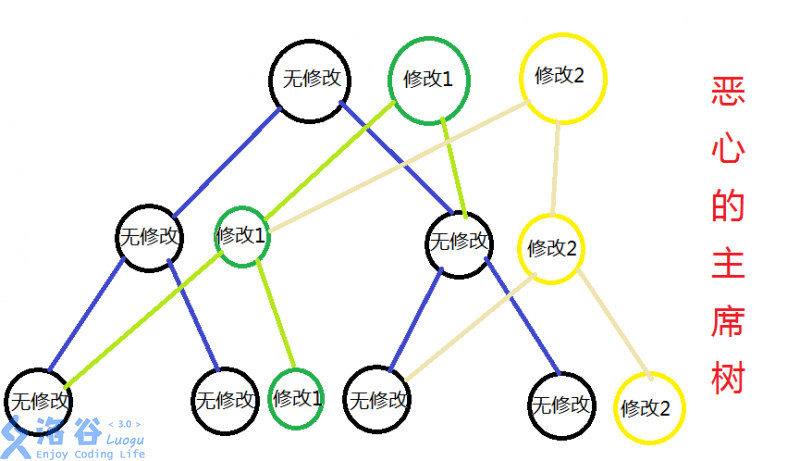
引用自:hyfhaha 的题解
具体地,从新的版本指针开始递归地新建节点,考虑每个节点的子节点维护的区间。对于不包含修改元素所在的区间,继承上个版本,直接将子节点指针指向上一个版本该位置的子节点即可。对于修改元素所在的区间,递归地新建节点,代码如下所示:
#define ls (lson[now_])
#define rs (rson[now_])
#define mid ((L_+R_)>>1)
void Modify(int &now_, int pre_, int L_, int R_, int pos_, int val_) {
now_ = ++ node_num; //每次都新建
if (L_ == R_) { //到达根
val[now_] = val_;
return ;
}
ls = lson[pre_], rs = rson[pre_]; //继承儿子
if (pos_ <= mid) Modify(ls, lson[pre_], L_, mid, pos_, val_); //修改
else Modify(rs, rson[pre_], mid + 1, R_, pos_, val_);
}
代码
//知识点:可持久化线段树
/*
By:Luckyblock
*/
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#define LL long long
const int kMaxn = 1e6 + 10;
//=============================================================
int n, m, a[kMaxn], root[kMaxn]; //root 为版本指针
//=============================================================
inline int read() {
int f = 1, w = 0;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-') f = -1;
for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
return f * w;
}
void Chkmax(int &fir_, int sec_) {
if (sec_ > fir_) fir_ = sec_;
}
void Chkmin(int &fir_, int sec_) {
if (sec_ < fir_) fir_ = sec_;
}
namespace Seg {
#define ls (lson[now_])
#define rs (rson[now_])
#define mid ((L_+R_)>>1)
int node_num, lson[kMaxn << 5], rson[kMaxn << 5], val[kMaxn << 5];
void Build(int &now_, int L_, int R_) {
now_ = ++ node_num;
if (L_ == R_) {
val[now_] = a[L_];
return ;
}
Build(ls, L_, mid);
Build(rs, mid + 1, R_);
}
void Modify(int &now_, int pre_, int L_, int R_, int pos_, int val_) {
now_ = ++ node_num;
if (L_ == R_) {
val[now_] = val_;
return ;
}
ls = lson[pre_];
rs = rson[pre_];
if (pos_ <= mid) Modify(ls, lson[pre_], L_, mid, pos_, val_);
else Modify(rs, rson[pre_], mid + 1, R_, pos_, val_);
}
int Query(int now_, int L_, int R_, int pos_) {
if (L_ == R_) return val[now_];
if (pos_ <= mid) return Query(ls, L_, mid, pos_);
return Query(rs, mid + 1, R_, pos_);
}
#undef ls
#undef rs
#undef mid
}
//=============================================================
int main() {
n = read(), m = read();
for (int i = 1; i <= n; ++ i) a[i] = read();
Seg::Build(root[0], 1, n);
for (int i = 1; i <= m; ++ i) {
int pre = read(), opt = read(), pos = read();
if (opt == 1) {
int val = read();
Seg::Modify(root[i], root[pre], 1, n, pos, val); //新建版本
} else {
printf("%d\n", Seg::Query(root[pre], 1, n, pos));
root[i] = root[pre]; //继承 root
}
}
return 0;
}
区间修改
通过标记永久化实现的区间修改可持久化线段树。
给定一长度为 \(n\) 的数列,给定 \(m\) 次操作。有一初始为 0 的时间戳。
- 区间加 \(d\),时间戳 + 1。
- 查询当前时间戳区间和。
- 查询给定时间戳区间和。
- 将当前时间戳置为给定时间戳。
所有操作均合法。
\(1\le n,m\le 10^5\),\(0|a_i|\le 10^9\),\(|d|\le 10^4\)。
829ms,1.46G。
区间修改区间查询的可持久化线段树。
考虑单点修改的可持久化线段树的原理:重用未被修改部分,仅新建被访问到的有变化的 \(\log n\) 个节点,并将新的版本指针指向新的根。
区间修改同理,一次区间修改至多会访问 \(2\log n\) 个节点,同样只新建这些节点,并更新版本指针即可。需要特别注意的是必须要标记永久化,否则下放标记时需要新建节点以保证版本之间互不影响,造成时空浪费。
总复杂度仍为 \(O(n\log n)\) 级别。
//知识点:可持久化线段树
/*
By:Luckyblock
*/
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#define LL long long
const int kN = 1e5 + 10;
//=============================================================
int n, m, now, a[kN];
//=============================================================
inline int read() {
int f = 1, w = 0;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-') f = -1;
for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
return f * w;
}
void Chkmax(int &fir, int sec) {
if (sec > fir) fir = sec;
}
void Chkmin(int &fir, int sec) {
if (sec < fir) fir = sec;
}
namespace Hjt {
#define ls lson[now_]
#define rs rson[now_]
#define mid ((L_+R_)>>1)
const int kMaxRoot = kN << 1;
const int kMaxNode = kN << 5;
int node_num, root[kMaxRoot], lson[kMaxNode], rson[kMaxNode];
LL tag[kMaxNode], sum[kMaxNode];
void Build(int &now_, int L_, int R_) {
now_ = ++ node_num;
if (L_ == R_) {
sum[now_] = a[L_];
return ;
}
Build(ls, L_, mid), Build(rs, mid + 1, R_);
sum[now_] = sum[ls] + sum[rs];
}
void Modify(int &now_, int pre_, int L_, int R_, int l_, int r_, int val_) {
now_ = ++ node_num;
lson[now_] = lson[pre_], rson[now_] = rson[pre_];
tag[now_] = tag[pre_], sum[now_] = sum[pre_];
sum[now_] += 1ll * (r_ - l_ + 1) * val_;
if (l_ == L_ && R_ == r_) {
tag[now_] += val_;
return ;
}
if (r_ <= mid) Modify(ls, lson[pre_], L_, mid, l_, r_, val_);
else if (l_ > mid) Modify(rs, rson[pre_], mid + 1, R_, l_, r_, val_);
else {
Modify(ls, lson[pre_], L_, mid, l_, mid, val_);
Modify(rs, rson[pre_], mid + 1, R_, mid + 1, r_, val_);
}
}
LL Query(int now_, int L_, int R_, int l_, int r_, LL tag_) {
if (l_ == L_ && R_ == r_) return sum[now_] + 1ll * (r_ - l_ + 1) * tag_;
if (r_ <= mid) return Query(ls, L_, mid, l_, r_, tag_ + tag[now_]);
else if (l_ > mid) return Query(rs, mid + 1, R_, l_, r_, tag_ + tag[now_]);
else return Query(ls, L_, mid, l_, mid, tag_ + tag[now_]) +
Query(rs, mid + 1, R_, mid + 1, r_, tag_ + tag[now_]);
}
}
//=============================================================
#define root Hjt::root
int main() {
n = read(), m = read(), now = 0;
for (int i = 1; i <= n; ++ i) a[i] = read();
Hjt::Build(root[0], 1, n);
for (int i = 1; i <= m; ++ i) {
char opt[5]; scanf("%s", opt);
if (opt[0] == 'C') {
++ now;
int l = read(), r = read(), val = read();
Hjt::Modify(root[now], root[now - 1], 1, n, l, r, val);
} else if (opt[0] == 'Q') {
int l = read(), r = read();
printf("%lld\n", Hjt::Query(root[now], 1, n, l, r, 0));
} else if (opt[0] == 'H') {
int l = read(), r = read(), t = read();
printf("%lld\n", Hjt::Query(root[t], 1, n, l, r, 0));
} else if (opt[0] == 'B') {
now = read();
}
}
return 0;
}
主席树
主席树,即可持久化权值线段树,维护“线段树的前缀和”。
给定一长度为 \(n\) 的数列 \(a\),给定 \(m\) 次询问。
每次询问给定参数 \(l,r,k\),查询数列 \(a\) 在闭区间 \([l,r]\) 内的第 \(k\) 小值。
\(1\le n,m\le 2\times 10^5\),\(|a_i|\le 10^9\),\(1\le l\le r\le n\),\(1\le k\le r-l+1\)。
1S ~ 1.2S,256MB。
先离散化,设数列最大值为 \(A\)。
考虑仅有一次询问的情况,yy 一下可得到这样一种解法:
对于区间 \([l,r]\),考虑排名 \(<k\) 的数的数量,考虑每次二分答案的值域 \([L, R]\),并检查区间 \([l,r]\) 中小于等于 \(\frac{L+R}{2}\) 的数,即左侧的数的个数 \(size\)。若 \(size<k\),则答案一定在值域 \([L, mid]\) 中,下调右端点。否则答案在 \([mid + 1, R]\) 中,且一定为其中排名第 \(k-size\) 的数,上调左端点。区间长度收缩至 \(1\) 时即得答案。
暴力实现的单次复杂度是 \(O(n\log A)\) 的。但这给出了一种思路:二分值域并检查数量。
看到二分值域检查数量,想到了权值线段树。假设已知区间 \([l,r]\) 建出的权值线段树,上面的二分完全可以在线段树上进行。
对于某节点维护的区间 \([L,R]\),其左右儿子分别维护的区间为 \(\left[L,\frac{L+R}{2}\right]\),\(\left[\frac{L+R}{2} + 1, R\right]\)。每次检查左儿子的 \(size\le k\) 是否成立。成立则答案必在左儿子,向左儿子递归。否则答案一定在右儿子,且一定是右儿子中排名 \(k-size\) 的数。令 \(k- size\),并向右儿子递归。递归至叶节点即得答案。
上述过程复杂度是 \(O(\log A)\) 的,非常喜人。
想办法怎么得到权值线段树。
考虑权值线段树构造的过程,在 \([l,r]\) 的权值线段树上插入 \(a_{r+1}\),即得 \([l,r+1]\) 的权值线段树。这玩意的形式和前缀和有些相似,不妨强行凑一凑。
考虑 \([1,l-1]\) 和 \([1,r]\) 的权值线段树,将它们对应位置节点维护信息相减。上述过程相当于删除 \([1,l-1]\) 的信息,发现这可以得到 \([l,r]\) 的权值线段树。于是可以考虑将 \(1\sim n\) 的前缀权值线段树全建出来,树上二分时 再将对应位置节点维护信息相减。单次查询的复杂度可以保证,但建树的时间和空间消耗较大。
发现 \([1,l]\) 和 \([1,l+1]\) 的权值线段树上,仅有 \(\log m\) 个节点不同。考虑可持久化线段树的套路,动态开点,并利用之前的线段树的信息。可以获得这样的结构:
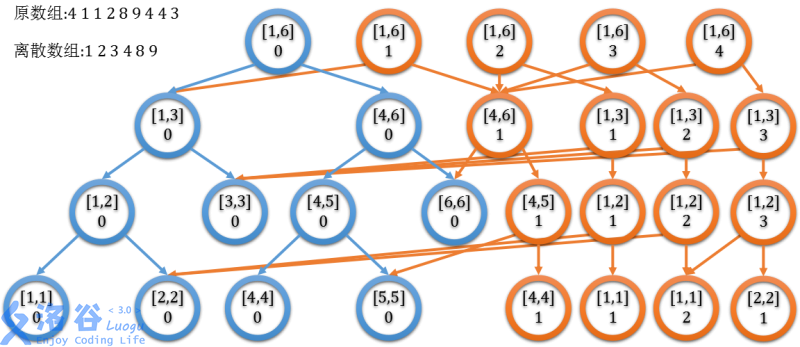
引用自:主席树 - 孤独·粲泽 的博客
这就是主席树,即可持久化权值线段树,用来维护“线段树的前缀和”,前缀线段树也满足可减性,从而得到任意区间构成的权值线段树。算法总空间复杂度为 \(O(n\log A)\),时间复杂度 \(O(m\log A)\)。
//知识点:主席树
/*
By:Luckyblock
*/
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#define LL long long
const int kMaxn = 2e5 + 10;
//=============================================================
int n, m, d_num, a[kMaxn], data[kMaxn], map[kMaxn];
int root[kMaxn];
//=============================================================
inline int read() {
int f = 1, w = 0;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-') f = -1;
for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
return f * w;
}
void Chkmax(int &fir_, int sec_) {
if (sec_ > fir_) fir_ = sec_;
}
void Chkmin(int &fir_, int sec_) {
if (sec_ < fir_) fir_ = sec_;
}
void Prepare() {
n = read(), m = read();
for (int i = 1; i <= n; ++i) {
a[i] = data[i] = read();
}
std::sort(data + 1, data + n + 1);
data[0] = -0x3f3f3f3f;
for (int i = 1; i <= n; ++i) {
if (data[i] != data[i - 1]) d_num++;
data[d_num] = data[i];
}
for (int i = 1; i <= n; ++i) {
int ori = a[i];
a[i] = std ::lower_bound(data + 1, data + d_num + 1, ori) - data;
map[a[i]] = ori;
}
}
namespace Hjt {
#define ls lson[now_]
#define rs rson[now_]
#define mid ((L_ + R_) >> 1)
int node_num, lson[kMaxn << 5], rson[kMaxn << 5], size[kMaxn << 5];
void Insert(int &now_, int pre_, int L_, int R_, int val_) {
now_ = ++node_num;
size[now_] = size[pre_] + 1;
ls = lson[pre_], rs = rson[pre_];
if (L_ == R_) return;
if (val_ <= mid)
Insert(ls, lson[pre_], L_, mid, val_);
else
Insert(rs, rson[pre_], mid + 1, R_, val_);
}
int Query(int r_, int l_, int L_, int R_, int k_) {
if (L_ == R_) return L_;
int sz = size[lson[r_]] - size[lson[l_]];
if (k_ <= sz)
return Query(lson[r_], lson[l_], L_, mid, k_);
else
return Query(rson[r_], rson[l_], mid + 1, R_, k_ - sz);
}
#undef ls
#undef rs
#undef mid
} // namespace Hjt
//=============================================================
int main() {
Prepare();
for (int i = 1; i <= n; ++i) {
Hjt::Insert(root[i], root[i - 1], 1, d_num, a[i]);
}
for (int i = 1; i <= m; ++i) {
int l = read(), r = read(), k = read();
printf("%d\n", map[Hjt::Query(root[r], root[l - 1], 1, d_num, k)]);
}
return 0;
}
带修主席树
主席树的本质是线段树的前缀和。前缀和的查询复杂度为 \(O(1)\) 级别,暴力单点修改复杂度 \(O(n)\) 级别。
考虑用树状数组平衡两者的复杂度。
给定一长度为 \(n\) 的数列 \(a\),给定 \(m\) 次操作。
操作有两种:
- 给定参数 \(x, y\),将 \(a_x\) 改为 \(y\)。
- 给定参数 \(l,r,k\),查询数列 \(a\) 在闭区间 \([l,r]\) 内的第 \(k\) 小值。
\(1\le n,m\le 10^5\),\(|a_i|\le 10^9\),\(1\le l\le r\le n\),\(1\le k\le r-l+1\)。
3S,512MB。
先离散化,设数的最大值为 \(m\)。
主席树的本质是权值线段树的前缀和。如果暴力修改,需要每次修改所有的位置,查询复杂度不变,修改复杂度为 \(O(n\log A)\)。
如何平衡前缀和的修改操作?考虑树状数组的思路,用二进制优化前缀和。
令第 \(k\) 棵权值线段树维护原来的 \([k-lowbit(k) + 1, k]\) 中的权值线段树。修改,查询时都查询 \(\log n\) 个权值线段树,每次查询修改复杂度为 \(O(\log^2 A)\)。空间复杂度不变,仍为 \(O(n\log A)\)。
一份很久之前写的很丑的代码:
//知识点:主席树,树状数组
/*
By:Luckyblock
*/
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#include <vector>
#define LL long long
const int kN = 1e6 + 10;
//=============================================================
struct Opt {
bool type;
int l, r, k, pos, val;
} q[kN];
int n, m, d_num, data[kN], num[kN];
std::vector <int> tmp1, tmp2;
//=============================================================
inline int read() {
int f = 1, w = 0;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-') f = -1;
for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
return f * w;
}
void Chkmax(int &fir, int sec) {
if (sec > fir) fir = sec;
}
void Chkmin(int &fir, int sec) {
if (sec < fir) fir = sec;
}
namespace Hjt {
#define ls lson[now_]
#define rs rson[now_]
#define mid ((L_+R_)>>1)
int node_num, root[kN], sz[kN << 5], lson[kN << 5], rson[kN << 5];
void Modify(int &now_, int L_, int R_, int pos_, int val_) {
if (!now_) now_ = ++ node_num;
sz[now_] += val_;
if (L_ == R_) return ;
if (pos_ <= mid) Modify(ls, L_, mid, pos_, val_);
else Modify(rs, mid + 1, R_, pos_, val_);
}
int Query(int L_, int R_, int k_) {
if (L_ == R_) return L_;
int sizel = 0;
for (int i = 0; i < tmp1.size(); ++ i) sizel -= sz[lson[tmp1[i]]];
for (int i = 0; i < tmp2.size(); ++ i) sizel += sz[lson[tmp2[i]]];
if (k_ <= sizel) {
for (int i = 0; i < tmp1.size(); ++ i) tmp1[i] = lson[tmp1[i]];
for (int i = 0; i < tmp2.size(); ++ i) tmp2[i] = lson[tmp2[i]];
return Query(L_, mid, k_);
}
for (int i = 0; i < tmp1.size(); ++ i) tmp1[i] = rson[tmp1[i]];
for (int i = 0; i < tmp2.size(); ++ i) tmp2[i] = rson[tmp2[i]];
return Query(mid + 1, R_, k_ - sizel);
}
}
namespace Bit {
#define low(x) (x&-x)
void Add(int pos_, int val_) {
int p = std::lower_bound(data + 1, data + d_num + 1, num[pos_]) - data;
for (int i = pos_; i <= n; i += low(i)) {
Hjt::Modify(Hjt::root[i], 1, d_num, p, val_);
}
}
int Query(int l_, int r_, int k_) {
tmp1.clear(), tmp2.clear();
for (int i = l_ - 1; i; i -= low(i)) tmp1.push_back(Hjt::root[i]);
for (int i = r_; i; i -= low(i)) tmp2.push_back(Hjt::root[i]);
return Hjt::Query(1, d_num, k_);
}
}
void Init() {
n = read(), m = read();
for (int i = 1; i <= n; ++ i) data[++ d_num] = num[i] = read();
for (int i = 1; i <= m; ++ i) {
char opt[5]; scanf("%s", opt + 1);
q[i].type = (opt[1] == 'Q');
if (q[i].type) {
q[i].l = read(), q[i].r = read(), q[i].k = read();
} else {
q[i].pos = read(), data[++ d_num] = q[i].val = read();
}
}
std::sort(data + 1, data + d_num + 1);
d_num = std::unique(data + 1, data + d_num + 1) - data - 1;
for (int i = 1; i <= n; ++ i) Bit::Add(i, 1);
}
//=============================================================
int main() {
Init();
for (int i = 1; i <= m; ++ i) {
if (q[i].type) {
int l = q[i].l, r = q[i].r, k = q[i].k;
printf("%d\n", data[Bit::Query(l, r, k)]);
} else {
int pos = q[i].pos, val = q[i].val;
Bit::Add(pos, -1);
num[pos] = val;
Bit::Add(pos, 1);
}
}
return 0;
}
在线静态二维数点
静态二维数点问题的模型:
给定平面上的 \(n\) 个点的坐标,第 \(i\) 个点的坐标为 \((xi,yi)\)。\(m\) 组询问,每次给定一个子矩阵,求子矩阵内点的数量。
可以考虑使用主席树解决,先将所有节点按照 \(x_i\) 排序,并按照排序后顺序依次插入到主席树中的位置 \(y_i\) 并建立新版本。
查询以 \((a,b)\) 为左上角,\((c,d)\) 为右下角的子矩阵时,先二分找到 \(x_i\) 大于等于 \(a\),小于等于 \(c\) 的第一个点 \(l\) 和最后一个点 \(r\),取出 \([l,r]\) 的权值线段树,查询线段树区间 \([c,d]\) 中点的数量即可。
正确性显然,总复杂度 \(O(n\log n + m\log n)\) 级别。
例题
「CTSC2018」混合果汁
二分答案,主席树
给定 \(n\) 个物品,物品 \(i\) 的数量为 \(l_i\),单个花费为 \(p_i\),价值为 \(d_i\)。
对于一个物品的选择方案,定义其总花费为所有物品的花费之和,其价值为方案中物品价值的最小值。
给定 \(m\) 个询问,每次询问给定参数 \(g,L\),求一个物品的选择方案,使得方案中物品数 \(\ge L\),花费 \(\le g\),且价值最大,输出最大的价值。
\(1\le n,m\le 10^5\),\(1\le d_i, p_i, l_i\le 10^5\),\(1\le g, L\le 10^{18}\)。
2S,512MB。
显然对于每个询问,答案满足单调性,考虑二分 选择方案中价值最小的物品 \(mid\)。 问题变为判定仅使用价值 \(\ge d_{mid}\) 的物品,总花费 \(\le g\) 时,能否选择 \(\ge L\) 个物品。
先考虑如何暴力 Check。二分答案之后,所有 可选物品 贡献均变为 1。 为满足花费限制,贪心的想,肯定先选花费小的。
则可将可选物品按花费升序排序,从小到大选择物品,直至不能再选,判断选择的数量是否 \(\ge L\) 即可。
单次 Check 复杂度 \(O(n\log n + n)\),总复杂度 \(O(mn\log^2 n)\),期望得分 \(45\text{pts}\)。
发现每次 Check 的过程中,我们仅关心某花费的物品的数量。考虑权值线段树维护对应权值区间内 物品的个数,与全部选择它们时的总花费。
每次 Check 时先将所有可选物品插入线段树中,再线段树上二分判断是否存在合法的方案。特别的,二分到叶节点后,注意特判叶节点选择的数量,因为叶节点对应的物品花费最高,可能不能全部选择。
单次 Check 复杂度变为 \(O(n\log n + \log n)\),总复杂度仍为 \(O(mn\log^2 n)\)。
发现上述过程的瓶颈在于,每次 Check 的 \(mid\) 不同导致可选物品都不同。必须每次重新构建 价值 \(\ge d_{mid}\) 的物品组成的权值线段树。
考虑可持久化,先将物品按 \(d_i\) 排序后 插入主席树中,Check 时直接取出对应部分即可,避免了重建线段树。
单次 Check 复杂度变为 \(O(\log^2 n)\),总复杂度 \(O(m\log^2 n)\),期望得分 \(100\text{pts}\)。
由于每次询问的 \(g,L\le 10^{18}\),保证了不会乘爆,注意开 long long。
//知识点:二分答案,主席树
/*
By:Luckyblock
*/
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstring>
#define ll long long
const int kMaxn = 1e5 + 10;
//=============================================================
struct Juice {
int d, p, l;
} a[kMaxn];
int n, m, maxp, ans, d[kMaxn], root[kMaxn];
ll g, L;
//=============================================================
inline ll read() {
ll f = 1, w = 0;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-') f = -1;
for (; isdigit(ch); ch = getchar()) w = (w << 3ll) + (w << 1ll) + (ch ^ '0');
return f * w;
}
bool CompareJuice(Juice fir, Juice sec) {
return fir.d < sec.d;
}
void Chkmax(int &fir_, int sec_) {
if (sec_ > fir_) fir_ = sec_;
}
void Chkmin(int &fir_, int sec_) {
if (sec_ < fir_) fir_ = sec_;
}
namespace Hjt {
#define ls lson[now_]
#define rs rson[now_]
#define mid ((L_+R_)>>1)
int node_num, lson[kMaxn << 5], rson[kMaxn << 5];
ll cnt[kMaxn << 5], val[kMaxn << 5];
void Insert(int &now_, int pre_, int L_, int R_, int pos_, int cnt_) {
now_ = ++ node_num;
lson[now_] = lson[pre_];
rson[now_] = rson[pre_];
cnt[now_] = cnt[pre_] + 1ll * cnt_;
val[now_] = val[pre_] + 1ll * pos_ * cnt_;
if (L_ == R_) return ;
if (pos_ <= mid) Insert(ls, lson[pre_], L_, mid, pos_, cnt_);
else Insert(rs, rson[pre_], mid + 1, R_, pos_, cnt_);
}
ll Query(int lnow_, int rnow_, int L_, int R_, ll k_) {
if (L_ == R_) {
return std :: min((1ll * k_ / L_), cnt[rnow_] - cnt[lnow_]);
}
ll vall = val[lson[rnow_]] - val[lson[lnow_]];
ll cntl = cnt[lson[rnow_]] - cnt[lson[lnow_]];
if (vall < k_) return Query(rson[lnow_], rson[rnow_], mid + 1, R_, k_ - vall) + cntl;
return Query(lson[lnow_], lson[rnow_], L_, mid, k_);
}
#undef mid
}
bool Check(int pos_) {
return Hjt :: Query(root[pos_ - 1], root[n], 1, maxp, g) >= L;
}
//=============================================================
int main() {
n = (int) read(), m = (int) read();
for (int i = 1; i <= n; ++ i) {
a[i] = (Juice) {(int) read(), (int) read(), (int) read()};
Chkmax(maxp, a[i].p);
d[i] = a[i].d;
}
std :: sort(a + 1, a + n + 1, CompareJuice);
for (int i = 1; i <= n; ++ i) {
Hjt :: Insert(root[i], root[i - 1], 1, maxp, a[i].p, a[i].l);
}
while (m --) {
g = read(), L = read(), ans = - 1;
for (int l = 1, r = n; l <= r; ) {
int mid = (l + r) >> 1;
if (Check(mid)) {
ans = a[mid].d;
l = mid + 1;
} else {
r = mid - 1;
}
}
printf("%d\n", ans);
}
return 0;
}
CF1436E Complicated Computations
主席树维护区间 \(\operatorname{mex}\)。
给定一长度为 \(n\) 的数列 \(a\),求其所有连续子序列的 \(\operatorname{mex}\) 的 \(\operatorname{mex}\)。
\(\operatorname{mex}(S)\) 定义为数集 \(S\) 中最小的没有出现的 正整数。
\(1\le a_i\le n\le 10^5\)。
1S,256MB。
设答案为 \(ans\),显然答案符合下列性质:
- 没有连续子序列的 \(\operatorname{mex}\) 为 \(ans\)。
- \(1\sim ans-1\) 都能够作为某连续子序列的 \(\operatorname{mex}\) 出现。
先考虑如何判断性质 1。
若某连续的子序列的 \(\operatorname{mex}\) 为 \(ans\),显然该连续子序列中不包括数 \(ans\),且连续子序列越长,越有可能满足条件。
考虑枚举所有不含 \(ans\) 的极长连续子序列进行判断,发现这些连续子序列即为整个数列 被所有 \(ans\) 分割成的子段。查询这些子段的 \(\operatorname{mex}\),判断是否等于 \(ans\) 即可。
再考虑性质 2,发现只需要从小到大枚举答案,重复对性质 1 的判断即可。
枚举到的第一个不满足性质 1 的即为答案。
考虑实现。
对于一个在数列中出现了 \(k\) 次的数,它可将数列分为 \(k+1\) 段,则总查询 \(\operatorname{mex}\) 次数为 \(O(n)\) 级别。
使用主席树,总时间复杂度为 \(O(n\log n)\) 级别。
使用莫队 + 值域分块,总时间复杂度 \(O(n\sqrt m + m\sqrt n)\)。
怎么用主席树实现啊/jk
第 \(i\) 棵主席树的叶节点 \(x\) 储存权值 \(x\) 在 \(a_{1}\sim a_{i}\) 中最晚出现的位置。 插入时只有单点修改,因此可以可持久化。
查询时查询第 \(r\) 棵主席树中最小的,最晚出现位置 \(<l\) 的权值,即为区间 \([l,r]\) 的 \(\operatorname{mex}\)。线段树维护区间最小值,主席树上二分即可。
//知识点:结论,主席树
/*
By:Luckyblock
*/
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#include <vector>
#define LL long long
const int kN = 1e5 + 10;
//=============================================================
int n, a[kN], root[kN];
std::vector <int> pos[kN];
//=============================================================
inline int read() {
int f = 1, w = 0;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-') f = -1;
for (; isdigit(ch); ch = getchar()) {
w = (w << 3) + (w << 1) + (ch ^ '0');
}
return f * w;
}
void Chkmax(int &fir_, int sec_) {
if (sec_ > fir_) fir_ = sec_;
}
void Chkmin(int &fir_, int sec_) {
if (sec_ < fir_) fir_ = sec_;
}
namespace Hjt {
#define ls (lson[now_])
#define rs (rson[now_])
#define mid (L_+R_>>1)
int node_num, lson[kN << 5], rson[kN << 5], t[kN << 5];
void Pushup(int now_) {
t[now_] = std::min(t[ls], t[rs]);
}
void Insert(int &now_, int pre_, int L_, int R_, int pos_, int val_) {
now_ = ++ node_num;
if (L_ == R_) {
t[now_] = val_;
return ;
}
ls = lson[pre_], rs = rson[pre_];
t[now_] = t[pre_];
if (pos_ <= mid) Insert(ls, lson[pre_], L_, mid, pos_, val_);
else Insert(rs, rson[pre_], mid + 1, R_, pos_, val_);
Pushup(now_);
}
int Query(int now_, int L_, int R_, int pos_) {
if (L_ == R_) return L_;
if (t[ls] < pos_) return Query(ls, L_, mid, pos_);
return Query(rs, mid + 1, R_, pos_);
}
#undef ls
#undef rs
#undef mid
}
//=============================================================
int main() {
n = read();
for (int i = 1; i <= n; ++ i) {
a[i] = read();
pos[a[i]].push_back(i);
Hjt::Insert(root[i], root[i - 1], 1, n + 1, a[i], i);
}
for (int i = 1; i <= n + 1; ++ i) pos[i].push_back(n + 1);
for (int i = 1; i <= n + 2; ++ i) {
int lim = pos[i].size(), flag = 0;
for (int j = 0, las = 1; j < lim; ++ j) {
int now = pos[i][j];
if (las < now) {
flag = (Hjt::Query(root[now - 1], 1, n + 1, las) == i);
if (flag) break;
}
las = now + 1;
}
if (! flag) {
printf("%d\n", i);
break;
}
}
return 0;
}
CF1422F Boring Queries
给定一长度为 \(n\) 的序列 \(a\),有 \(q\) 次询问。
每次询问给定区间 \([l,r]\),求 \(\operatorname{lcm}(a_l, \cdots,a_{r}) \bmod 10^9 + 7\)。
强制在线。
\(1\le n,q\le 10^5\),\(1\le a_i\le 2\times 10^5\)。
3S,512MB。
算法一
首先对 \(a\) 质因数分解,设 \(a_i\) 分解后为 \(\prod\limits_j p_j^{c_{i,j}}\)
根据小学奥数,有:
如果不强制在线,用莫队维护下各质因子出现次数即可。
但恶心出题人强制在线,期望得分 0pts。
算法二
发现算法一中有区间取 \(\max\) 的操作,考虑对每个质因子都建立一棵线段树,维护区间该质因子次数的最大值。查询时枚举质因子,累乘贡献即可。
时空复杂度 \(O(kn\log n)\),\(k\) 为质因子个数,可知 \(k \approx \frac{n}{\ln n}\),时间空间均无法承受,期望得分 0pts。
算法三
发现数的值域比较小,又出现了质因子这样的字眼,考虑套路根号分治。
先将不大于 \(\sqrt{2\times 10^5}\) 的质因子筛出,发现仅有 92 个,于是仅建立 92 棵线段树,套用算法二,维护区间该质因子次数最大值。
再考虑大于 \(\sqrt{2\times 10^5}\) 的质因子,它们在每个 \(a_i\) 中的次数最多为 1,取 \(\max\) 后次数也只能为 1。
则每种质因子只能贡献一次,查询区间内它们的贡献,即为查询区间内 不同权值 的乘积。
这是个经典问题,可以看这里统计区间里有多少个不同的数__莫队__主席树__树状数组_dctika1584的博客。不强制在线可以用线段树 + 扫描线,通过单点修改维护。强制在线,套路地可持久化即可。
总时空间复杂度均为 \(O(kn\log n + n\log^2 n)\),\(k=92\),能过。
对于不大于 \(\sqrt{2\times 10^5}\) 的质因子,质因子的幂 \(\le 2\times 10^5\),因此代码中直接维护了该质因子的幂的最大值,而不是上述的次数。
//知识点:线段树,主席树
/*
By:Luckyblock
注意在维护较小质因子的线段树中不能取模
合并的时候写的乘,并非取最大值。
我是,傻逼,哈哈。
*/
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#define LL long long
const int kN = 1e5 + 10;
const int kMax = 2e5;
const int mod = 1e9 + 7;
//=============================================================
int p_num, p[kMax + 10];
bool vis[kMax + 10];
int n, m, ans, a[kN], last[kN], lastv[kMax];
int root[kN];
//=============================================================
inline int read() {
int f = 1, w = 0;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-') f = -1;
for (; isdigit(ch); ch = getchar()) {
w = (w << 3) + (w << 1) + (ch ^ '0');
}
return f * w;
}
void Chkmax(int &fir_, int sec_) {
if (sec_ > fir_) fir_ = sec_;
}
void Chkmin(int &fir_, int sec_) {
if (sec_ < fir_) fir_ = sec_;
}
void Euler() {
for (int i = 2; i <= kMax; ++ i) {
if (! vis[i]) p[++ p_num] = i;
for (int j = 1; j <= p_num && i * p[j] <= kMax; ++ j) {
vis[i * p[j]] = true;
if (i % p[j] == 0) break;
}
}
}
int QPow(int x_, int y_) {
x_ %= mod;
int ret = 1;
for (; y_; y_ >>= 1) {
if (y_ & 1) ret = 1ll * ret * x_ % mod;
x_ = 1ll * x_ * x_ % mod;
}
return ret;
}
int Inv(int x_) {
return QPow(x_, mod - 2);
}
namespace Hjt {
#define ls (lson[now_])
#define rs (rson[now_])
#define mid ((L_+R_)>>1)
int node_num, lson[kN << 6], rson[kN << 6], t[kN << 6];
void Init() {
t[0] = 1;
}
void Insert(int &now_, int pre_, int L_, int R_, int pos_, int val_) {
now_ = ++ node_num;
t[now_] = 1ll * t[pre_] * val_ % mod;
if (L_ == R_) return ;
ls = lson[pre_], rs = rson[pre_];
if (pos_ <= mid) Insert(ls, lson[pre_], L_, mid, pos_, val_);
else Insert(rs, rson[pre_], mid + 1, R_, pos_, val_);
}
int Query(int now_, int L_, int R_, int l_, int r_) {
if (l_ <= L_ && R_ <= r_) return t[now_];
int ret = 1;
if (l_ <= mid) ret = 1ll * ret * Query(ls, L_, mid, l_, r_) % mod;
if (r_ > mid) ret = 1ll * ret * Query(rs, mid + 1, R_, l_, r_) % mod;
return ret;
}
#undef ls
#undef rs
#undef mid
}
#define ls (now_<<1)
#define rs (now_<<1|1)
#define mid ((L_+R_)>>1)
struct Seg {
int t[kN << 2];
void Build(int now_, int L_, int R_) {
t[now_] = 1;
if (L_ == R_) return ;
Build(ls, L_, mid);
Build(rs, mid +1, R_);
}
void Pushup(int now_) {
t[now_] = std::max(t[ls], t[rs]);
}
void Insert(int now_, int L_, int R_, int pos_, int val_) {
if (L_ == R_) {
t[now_] = val_;
return ;
}
if (pos_ <= mid) Insert(ls, L_, mid, pos_, val_);
else Insert(rs, mid + 1, R_, pos_, val_);
Pushup(now_);
}
int Query(int now_, int L_, int R_, int l_, int r_) {
if (l_ <= L_ && R_ <= r_) return t[now_];
int ret = 1;
if (l_ <= mid) Chkmax(ret, Query(ls, L_, mid, l_, r_));
if (r_ > mid) Chkmax(ret, Query(rs, mid + 1, R_, l_, r_));
return ret;
}
} t[93];
#undef ls
#undef rs
#undef mid
void Insert(int pos_) {
int val = a[pos_] = read();
for (int i = 1; p[i] * p[i] <= kMax; ++ i) {
int d = p[i], delta = 1;
if (val == 1) break;
if (val % d) continue ;
while (val % d == 0) {
val /= d;
delta *= d;
}
t[i].Insert(1, 1, n, pos_, delta);
}
root[pos_] = root[pos_ - 1];
Hjt::Insert(root[pos_], root[pos_], 1, n, pos_, val);
if (lastv[val]) Hjt::Insert(root[pos_], root[pos_], 1, n, lastv[val], Inv(val));
lastv[val] = pos_;
}
int Query(int l_, int r_) {
int ret = 1;
for (int i = 1; p[i] * p[i] <= kMax; ++ i) {
ret = 1ll * ret * std::max(1, t[i].Query(1, 1, n, l_, r_)) % mod;
}
ret = 1ll * ret * Hjt::Query(root[r_], 1, n, l_, r_) % mod;
return ret;
}
void Prepare() {
Euler();
Hjt::Init();
n = read();
for (int i = 1; i <= n; ++ i) Insert(i);
}
//=============================================================
int main() {
Prepare();
m = read();
while (m --) {
int l = (read() + ans) % n + 1, r = (read() + ans) % n + 1;
if (l > r) std::swap(l, r);
printf("%d\n", ans = Query(l, r));
}
return 0;
}
P2839 [国家集训队]middle
二分答案,可持久化对象的多样性。
对于一长度为 \(n\) 的数列 \(a\),定义其「中位数」为排序后数列的第 \(\frac{n}{2}\) 个数,下标从 0 开始。
给定一长度为 \(n\) 的数列 \(a\),\(q\) 次询问,每次询问给定参数 \(a,b,c,d\),保证 \(a<b<c<d\)。求区间左端点在 \([a,b]\) 之间,右端点在 \([c,d]\) 之间的子区间中,最大的「中位数」,「中位数」的定义见上文。
强制在线。
\(1\le n\le 2\times 10^4\),\(1\le q\le 2.5\times 10^4\)。
2S,512MB。
国际惯例先离散化,以下均在离散化的前提下展开。
对于一个询问 \((a,b,c,d)\),可拆成三部分考虑:\([b,c]\) 内必选的部分和 \([a,b)\) 的一段后缀,\((c,d]\) 的一段前缀。仅需考虑什么样的前后缀 对答案有贡献即可。
假设已选出一段区间 \([l,r]\),有 \(a<l\le b\),\(c\le r<d\),设其中位数为 \(mid\)。显然,此时从左右两侧向区间内添加不小于 \(mid\) 的数可能会使中位数增大,添加小于 \(mid\) 的数可能会使中位数减小。
手玩一下可发现,当且仅当 添加的不小于 \(mid\) 的数的个数 大于等于 添加的小于 \(mid\) 的个数时,中位数才可能增大。不小于 \(mid\) 的数的个数 比小于 \(mid\) 的数的个数越多,贡献就越大。
下文将一个区间中不小于 \(mid\) 的个数与小于 \(mid\) 的个数 的差值称为该区间的贡献。
之后怎么做?动态维护中位数,找到左右两侧对 当前中位数 贡献最大的前后缀加入?发现不好搞,因为中位数变化后,贡献也在变化。
考虑枚举固定一个中位数的 下界,从而固定前后缀的贡献。以此下界为据,加入左右两侧贡献最大的前后缀。判断最后的中位数是否满足大于该下界。
若满足,说明答案 \(\ge\) 该下界,可调高下界,否则需要调低下界。发现该 中位数的下界 满足单调性,可二分答案枚举 \(mid\)。
发现选择 1 个不小于 \(mid\) 的数 和 1 个小于 \(mid\) 的数贡献会相互抵消。更形象地,1 个不小于 \(mid\) 的数的 贡献 为 1,选择 1 个小于 \(mid\) 的数的 代价 也为 1。由此,枚举下界后,考虑条件转换:将区间 \([a,d]\) 内不小于 \(mid\) 的数变为 1,小于 \(mid\) 的数变为 -1。此时一段区间的贡献变为该区间转化后的和。
单次 Check 需要解决的问题变为:判断转化后的数列,\([b,c]\) 的和 + \([a,b)\) 的最大后缀和 + \((c,d]\) 的最大前缀和,是否不小于 \(0\)。暴力实现单次 Check 的复杂度为 \(O(n)\),总复杂度为 \(O(qn\log n)\),过不了。
地球人都知道最大前后缀和可以用线段树维护:SP1043 GSS1 - Can you answer these queries I。
考虑预处理每一个二分的下界对应的数列,并建出线段树。这样单次 Check 的复杂度变为 \(O(\log n)\),询问的复杂度变为 \(O(q\log^2 n)\)。
但预处理 \(n\) 棵线段树空间,时间都是 \(O(n^2 \log n)\) 的,还是很菜,过不了。
下面是一个很神的优化 (不愧是clj)。
考虑二分答案枚举的下界 \(mid\),发现对于下界为 \(mid\) 与 \(mid+1\) 时的数列,仅有 \(a_i = mid\) 的位置不同,由 1 变为了 -1。再观察上面建的 \(n\) 棵线段树,由上可知,对于第 \(mid\) 棵与第 \(mid+1\) 棵,仅有\(a_i = mid\) 的位置不同。
考虑对 二分值 进行可持久化,从而压缩线段树空间。 离散化后二分值最多仅有 \(n\) 种取值,预处理的空间时间均压缩为 \(O(n\log n)\) 级别。再套用上面的查询,总复杂度为 \(O(n\log n + q\log^2 n)\),可过。
注意可持久化线段树的实际含义。
root 的下标是 二分值,因此构建 root[i] 时,修改对象为 \(a_j<i\) 的位置。
//知识点:二分答案,可持久化线段树
/*
By:Luckyblock
*/
#include <algorithm>
#include <cctype>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <vector>
#define ll long long
const int kMaxn = 2e4 + 10;
//=============================================================
struct Node {
int sum, lmax, rmax;
};
int n, q, ans, a[kMaxn], root[kMaxn];
int data_num, data[kMaxn], map[kMaxn];
//=============================================================
inline int read() {
int f = 1, w = 0;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-') f = -1;
for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
return f * w;
}
void Chkmax(int &fir_, int sec_) {
if (sec_ > fir_) fir_ = sec_;
}
void Chkmin(int &fir_, int sec_) {
if (sec_ < fir_) fir_ = sec_;
}
namespace Seg {
#define ls (lson[now_])
#define rs (rson[now_])
#define mid ((L_+R_)>>1)
int node_num, lson[kMaxn << 5], rson[kMaxn << 5];
int sum[kMaxn << 5], lmax[kMaxn << 5], rmax[kMaxn << 5];
void Debug(int now_, int L_, int R_) {
printf("%d %d:%d %d %d\n", L_, R_, sum[now_], lmax[now_], rmax[now_]);
if (L_ == R_) {
return ;
}
Debug(ls, L_, mid);
Debug(rs, mid + 1, R_);
}
void Pushup(int now_) {
sum[now_] = sum[ls] + sum[rs];
lmax[now_] = std::max(lmax[ls], sum[ls] + lmax[rs]);
rmax[now_] = std::max(rmax[ls] + sum[rs], rmax[rs]);
}
void Build(int &now_, int L_, int R_) {
now_ = ++ node_num;
if (L_ == R_) {
lmax[now_] = rmax[now_] = sum[now_] = 1;
return ;
}
Build(ls, L_, mid);
Build(rs, mid + 1, R_);
Pushup(now_);
}
void Modify(int &now_, int pre_, int L_, int R_, int pos_) {
now_ = ++ node_num;
ls = lson[pre_], rs = rson[pre_];
if (L_ == R_) {
lmax[now_] = rmax[now_] = 0;
sum[now_] = -1;
return ;
}
if (pos_ <= mid) Modify(ls, lson[pre_], L_, mid, pos_);
else Modify(rs, rson[pre_], mid + 1, R_, pos_);
Pushup(now_);
}
Node Merge(Node l_, Node r_) {
Node ret = (Node) {0, 0, 0};
ret.sum = l_.sum + r_.sum;
ret.lmax = std::max(l_.lmax, l_.sum + r_.lmax);
ret.rmax = std::max(l_.rmax + r_.sum, r_.rmax);
return ret;
}
Node Query(int now_, int L_, int R_, int l_, int r_) {
if (l_ > r_) return (Node) {0, 0, 0};
if (l_ <= L_ && R_ <= r_) {
return (Node) {sum[now_], lmax[now_], rmax[now_]};
}
if (r_ <= mid) return Query(ls, L_, mid, l_, r_);
if (l_ > mid) return Query(rs, mid + 1, R_, l_, r_);
return Merge(Query(ls, L_, mid, l_, mid), Query(rs, mid + 1, R_, mid + 1, r_));
}
#undef ls
#undef rs
#undef mid
}
void Prepare() {
n = read();
for (int i = 1; i <= n; ++ i) a[i] = data[i] = read();
std::sort(data + 1, data + n + 1);
data_num = 1;
map[1] = data[1];
for (int i = 2; i <= n; ++ i) {
if (data[i] != data[i - 1]) {
map[++ data_num] = data[i];
}
data[data_num] = data[i];
}
std :: vector <int> pos[kMaxn];
for (int i = 1; i <= n; ++ i) {
a[i] = std::lower_bound(data + 1, data + data_num + 1, a[i]) - data;
pos[a[i]].push_back(i);
}
Seg::Build(root[1], 1, n);
for (int i = 2; i <= data_num; ++ i) {
root[i] = root[i - 1];
for (int j = 0, lim = pos[i - 1].size(); j < lim; ++ j) {
Seg::Modify(root[i], root[i], 1, n, pos[i - 1][j]);
}
}
}
bool Check(int ll_, int lr_, int rl_, int rr_, int lim_) {
int sum = Seg::Query(root[lim_], 1, n, lr_, rl_).sum;
int suml = Seg::Query(root[lim_], 1, n, ll_, lr_ - 1).rmax;
int sumr = Seg::Query(root[lim_], 1, n, rl_ + 1, rr_).lmax;
return (sum + suml + sumr) >= 0;
}
void Query(int ll_, int lr_, int rl_, int rr_) {
for (int l = 1, r = data_num; l <= r; ) {
int mid = ((l + r) >> 1);
if (Check(ll_, lr_, rl_, rr_, mid)) {
ans = map[mid];
l = mid + 1;
} else {
r = mid - 1;
}
}
}
//=============================================================
int main() {
Prepare();
q = read();
for (int i = 1; i <= q; ++ i) {
int opt[4];
for (int j = 0; j < 4; ++ j) {
opt[j] = (read() + ans) % n;
}
std::sort(opt, opt + 4);
Query(opt[0] + 1, opt[1] + 1, opt[2] + 1, opt[3] + 1);
printf("%d\n", ans);
}
return 0;
}
「TJOI / HEOI2016」字符串
二分答案,SA + 主席树
给定一长度为 \(n\) 的字符串,\(m\) 个询问。
每次询问给定参数 \(a,b,c,d\),求子串 \(S[a:b]\) 的所有子串,与子串 \(S[c:d]\) 的最长公共前缀的最大值。
\(1\le n,m\le 10^5, 1\le a\le b\le n, 1\le c\le d\le n\)。
对于每一个询问,答案满足单调性,考虑二分答案。 设 \(l\) 为当前二分到的最长的,子串 \(S[a:b]\) 的 所有子串,与子串 \(S[c:d]\) 的最长公共前缀。
分析可知,若 \(l\) 合法,那么会存在至少一个后缀 \(x\) 满足:
- 开头在 \([a:b-l+1]\) 中。
- \(\operatorname{lcp}(x, c)\ge l\)。
对于第二个限制,考虑 \(\operatorname{lcp}\) 的单调性。\(\operatorname{lcp}(x,c)\) 是一个在 \(c\) 处取极值的单峰函数。
则满足条件的 \(x\) 的取值,一定是 \(sa\) 数组上连续的一段。
套路地对 \(\operatorname{height}\) 建立 st 表,即可 \(O(1)\) 查询 \(\operatorname{lcp}\),于是可以通过二分排名快速得到后缀 \(x\) 排名的取值范围,将限制二也转化为了区间限制形式。
限制一限制了后缀的区间,限制二限制了 \(rk\) 的区间。查询这样的后缀的存在性,变成了一个静态二维数点问题。
对 \(sa\) 数组建立主席树维护即可。
//知识点:SA,二分答案,主席树
/*
By:Luckyblock
*/
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <ctype.h>
#define ll long long
const int kMaxn = 1e5 + 10;
//=============================================================
char S[kMaxn];
int n, m, ans, cnt[kMaxn], id[kMaxn], rkid[kMaxn];
int sa[kMaxn], rk[kMaxn << 1], oldrk[kMaxn << 1], height[kMaxn];
int MaxHeight[kMaxn][20], Log2[kMaxn];;
int lson[kMaxn << 5], rson[kMaxn << 5], size[kMaxn << 5];
int node_num, root[kMaxn];
//=============================================================
inline int read() {
int f = 1, w = 0; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') f = -1;
for (; isdigit(ch); ch = getchar()) w = (w << 3) + (w << 1) + (ch ^ '0');
return f * w;
}
void GetMax(int &fir, int sec) {
if (sec > fir) fir = sec;
}
bool cmp(int x, int y, int w) { //判断两个子串是否相等。
return oldrk[x] == oldrk[y] &&
oldrk[x + w] == oldrk[y + w];
}
void GetHeight() {
for (int i = 1, k = 0; i <= n; ++ i) {
if (rk[i] == 1) k = 0;
else {
if (k > 0) k --;
int j = sa[rk[i] - 1];
while (i + k <= n && j + k <= n &&
S[i + k] == S[j + k]) {
++ k;
}
}
height[rk[i]] = k;
}
}
int QueryLcp(int l_, int r_) {
int k = Log2[r_ - l_ + 1];
return std :: min(MaxHeight[l_][k], MaxHeight[r_ - (1 << k) + 1][k]);
}
void MakeSt() {
for (int i = 2; i <= n; ++ i) MaxHeight[i][0] = height[i];
for (int i = 2; i <= n; ++ i) {
Log2[i] = Log2[i >> 1] + 1;
}
for (int j = 1; j < 20; ++ j) {
for (int i = 1; i + (1 << j) - 1 <= n; ++ i) {
MaxHeight[i][j] = std :: min(MaxHeight[i][j - 1],
MaxHeight[i + (1 << (j - 1))][j - 1]);
}
}
}
void SuffixSort() {
int M = 300;
for (int i = 1; i <= n; ++ i) ++ cnt[rk[i] = S[i]];
for (int i = 1; i <= M; ++ i) cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; -- i) sa[cnt[rk[i]] --] = i;
for (int p, w = 1; w < n; w <<= 1) {
p = 0;
for (int i = n; i > n - w; -- i) id[++ p] = i;
for (int i = 1; i <= n; ++ i) {
if (sa[i] > w) id[++ p] = sa[i] - w;
}
memset(cnt, 0, sizeof (cnt));
for (int i = 1; i <= n; ++ i) ++ cnt[(rkid[i] = rk[id[i]])];
for (int i = 1; i <= M; ++ i) cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; -- i) sa[cnt[rkid[i]] --] = id[i];
std ::swap(rk, oldrk);
M = 0;
for (int i = 1; i <= n; ++ i) {
M += (cmp(sa[i], sa[i - 1], w) ^ 1);
rk[sa[i]] = M;
}
}
GetHeight();
MakeSt();
}
void Insert(int pre_, int &now_, int L_, int R_, int val_) {
now_ = ++ node_num;
size[now_] = size[pre_] + 1;
lson[now_] = lson[pre_], rson[now_] = rson[pre_];
if(L_ >= R_) return ;
int mid = (L_ + R_) >> 1;
if(val_ > mid) Insert(rson[pre_], rson[now_], mid + 1, R_, val_);
else Insert(lson[pre_], lson[now_], L_, mid, val_);
}
int Query(int u_, int v_, int L_, int R_, int ql_, int qr_) {
if (ql_ <= L_ && R_ <= qr_) return size[v_] - size[u_];
int mid = (L_ + R_) >> 1, ret = 0;
if (ql_ <= mid) ret += Query(lson[u_], lson[v_], L_, mid, ql_, qr_);
if (qr_ > mid) ret += Query(rson[u_], rson[v_], mid + 1, R_, ql_, qr_);
return ret;
}
bool Judge(int len_, int a_, int b_, int c_) {
int l = 1, r = rk[c_], up, down;
while (l < r) {
int mid = (l + r) >> 1;
if (QueryLcp(mid + 1, rk[c_]) < len_) l = mid + 1;
else r = mid;
}
up = r, l = rk[c_], r = n;
while (l < r) {
int mid = (l + r + 1) >> 1;
if (QueryLcp(rk[c_] + 1, mid) < len_) r = mid - 1;
else l = mid;
}
down = r;
return Query(root[up - 1], root[down], 1, n, a_, b_ - len_ + 1) > 0;
}
int Solve(int a_, int b_, int c_, int d_) {
int l = 0, r = std :: min(b_ - a_ + 1, d_ - c_ + 1);
while (l < r) {
int len = (l + r + 1) >> 1;
if (Judge(len, a_, b_, c_)) l = len;
else r = len - 1;
}
return r;
}
//=============================================================
int main() {
n = read(), m = read();
scanf("%s", S + 1);
SuffixSort();
for (int i = 1; i <= n; ++ i) Insert(root[i - 1], root[i], 1, n, sa[i]);
for (int i = 1; i <= m; ++ i) {
int a = read(), b = read(), c = read(), d = read();
printf("%d\n", Solve(a, b, c, d));
}
return 0;
}
「十二省联考 2019」字符串问题
SA,可持久化线段树优化建图,DAGDP
\(T\) 组数据,每次给定一字符串 \(S\)。
在 \(S\) 中存在 \(n_a\) 个 A 类子串 \((la_i, ra_i)\),\(n_b\) 个 B 类子串 \((lb_i,rb_i)\)。且存在 \(m\) 组支配关系,支配关系 \((x,y)\) 表示第 \(x\) 个 A 类串支配第 \(y\) 个 B 类串。
要求构造一个目标串 \(T\),满足:
- \(T\) 由若干 A 类串拼接而成。
- 对于分割中所有相邻的串,后一个串存在一个被前一个串支配的前缀。
求该目标串的最大长度,若目标串可以无限长输出 \(-1\)。
\(1\le T\le 100\),\(n_a,n_b,|S|,m\le 2\times 10^5\)。
6S,1G。
首先建立图论模型,从每个 A 类子串向其支配的 B 串连边,从每个 B 串向以它为前缀的 A 串连边。A 串节点的权值为其长度,B 串节点权值为 0。
在图上 DP 求得最长路即为答案,若图中存在环则无解。
第一类边有 \(m\) 条,但第二类边数可以达到 \(n_an_b\) 级别,考虑优化建图。
对于某 A 串 \((la_i, ra_i)\),它以 B 串 \((lb_j, rb_j)\) 作为一个前缀的充要条件是 \(\operatorname{lcp}(S[la_i:n],S[lb_j:n]) \ge rb_j-lb_j+1\) 且 \(ra_i - la_i + 1\ge rb_j-lb_j+1\)。
对于限制一,考虑求得 \(S\) 的 SA,对 \(\operatorname{height}\) 建立 ST 表,可在 \(sa\) 上二分求得满足 \(\operatorname{lcp}\ge rb_j-lb_j+1\) 的区间的左右边界,满足条件的 A 串一定都在这段区间内。第二类边转化为区间连边问题。
此时不考虑限制二直接线段树优化建图,可以拿到 80 分的好成绩。
限制二实际上限定了 B 连边的对象的长度。
考虑将所有 A,B 串按长度递减排序,按长度递减枚举 A 串并依次加入可持久化线段树。
对于每一个 B 串,先找到使得 A 串长度大于其长度的最晚的历史版本,此时线段树上的所有 A 串长度都大于其长度,再向这棵线段树上的节点连边。
时间复杂度 \(O((|S| + n_a + n_b)\log n)\),空间复杂度 \(O(m + (|S| + n_a + n_b)\log n)\),不需要刻意卡常就能稳过。
看见上面轻描淡写的是不是觉得这题太傻逼了?以下是菜鸡 Lb 在代码实现上的小问题。
边数在极限数据下可以达到 \(10^7\) 级别,不注意空间大小和清空时的实现会被卡到 60。这个时空限制显然就是给选手乱搞的,数组往大了开就行。
在线段树优化建图中,实点会在建树操作中就与虚点连好边。本题的实点是代表 A,B 串的节点,在本题的可持久化线段树优化中,实点与虚点的连边发生在动态开点的插入过程中。
在新建节点时,需要将该节点连向上一个版本中对应位置的节点。
对于 A 串 \((la_i, ra_i)\),它应该被插入到线段树中 \(rk_{la_i}\) 的位置,即叶节点 \(rk_{la_i}\) 与该实点相连。
\(\operatorname{height}_1\) 没有意义。
注意二分时的初始值。
long long
函数传参顺序 是通过栈传递的,因此是从右向左的。
//知识点:SA,可持久化线段树,优化建图,DAGDP
/*
By:Luckyblock
*/
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#include <queue>
#define LL long long
const int kN = 2e5 + 10;
//=============================================================
struct Str {
int l, r, lth, id;
} subs[kN << 1];
int node_num, n, na, nb, m, into[kN <<5];
int e_num, head[kN << 5], v[50 * kN], ne[50 * kN];
LL val[kN << 5], f[kN << 5];
char s[kN];
//=============================================================
inline int read() {
int f = 1, w = 0;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-') f = -1;
for (; isdigit(ch); ch = getchar()) {
w = (w << 3) + (w << 1) + (ch ^ '0');
}
return f * w;
}
void Chkmax(LL &fir_, LL sec_) {
if (sec_ > fir_) fir_ = sec_;
}
void Chkmin(int &fir_, int sec_) {
if (sec_ < fir_) fir_ = sec_;
}
bool cmp(Str fir_, Str sec_) {
if (fir_.lth != sec_.lth) return fir_.lth > sec_.lth;
return fir_.id < sec_.id;
}
void Add(int u_, int v_) {
v[++ e_num] = v_, ne[e_num] = head[u_], head[u_] = e_num;
into[v_] ++;
}
namespace ST {
int Minn[kN][21], Log2[kN];
void MakeST(int *a_) {
for (int i = 1; i <= n; ++ i) Minn[i][0] = a_[i];
for (int i = 2; i <= n; ++ i) Log2[i] = Log2[i >> 1] + 1;
for (int j = 1; j <= 20; ++ j) {
for (int i = 1; i + (1 << j) - 1 <= n; ++ i) { //
Minn[i][j] = std::min(Minn[i][j - 1], Minn[i + (1 << (j - 1))][j - 1]);
}
}
}
int Query(int l_, int r_) {
int k = Log2[r_ - l_ + 1];
return std::min(Minn[l_][k], Minn[r_ - (1 << k) + 1][k]);
}
}
namespace SA {
int sa[kN], rk[kN << 1];
int oldrk[kN << 1], cnt[kN], id[kN];
int height[kN];
void SuffixSort() {
int rknum = std::max(n, 300);
memset(cnt, 0, sizeof (cnt));
for (int i = 1; i <= n; ++ i) cnt[rk[i] = s[i]] ++;
for (int i = 1; i <= rknum; ++ i) cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; -- i) sa[cnt[rk[i]] --] = i;
for (int w = 1, p; w < n; w <<= 1) {
p = 0;
for (int i = n; i > n - w; -- i) id[++ p] = i;
for (int i = 1; i <= n; ++ i) {
if (sa[i] > w) id[++ p] = sa[i] - w;
}
memset(cnt, 0, sizeof (cnt));
for (int i = 1; i <= n; ++ i) ++ cnt[rk[id[i]]];
for (int i = 1; i <= rknum; ++ i) cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; -- i) sa[cnt[rk[id[i]]] --] = id[i];
for (int i = 1; i <= n; ++ i) oldrk[i] = rk[i];
rknum = 0;
for (int i = 1; i <= n; ++ i) {
rknum += (oldrk[sa[i]] == oldrk[sa[i - 1]] &&
oldrk[sa[i] + w] == oldrk[sa[i - 1] + w]) ^ 1;
rk[sa[i]] = rknum;
}
}
}
void GetHeight() {
for (int i = 1, k = 0; i <= n; ++ i) {
if (rk[i] == 1) {
k = 0;
} else {
if (k) -- k;
int j = sa[rk[i] - 1];
while (i + k <= n && j + k <= n &&
s[i + k] == s[j + k]) {
++ k;
}
}
height[rk[i]] = k;
}
}
int Lcp(int x_, int y_) {
if (x_ > y_) std::swap(x_, y_);
return ST::Query(x_ + 1, y_);
}
void Init() {
SuffixSort();
GetHeight();
ST::MakeST(SA::height);
}
}
namespace Hjt {
#define ls lson[now_]
#define rs rson[now_]
#define mid ((L_+R_)>>1)
int root[kN], lson[kN << 5], rson[kN << 5];
void Insert(int &now_, int pre_, int L_, int R_, int pos_, int id_) {
now_ = ++ node_num;
ls = lson[pre_], rs = rson[pre_];
if (pre_) Add(now_, pre_);
if (L_ == R_) {
Add(now_, id_);
return ;
}
if (pos_ <= mid) {
Insert(ls, lson[pre_], L_, mid, pos_, id_);
Add(now_, ls);
} else {
Insert(rs, rson[pre_], mid + 1, R_, pos_, id_);
Add(now_, rs);
}
}
void AddEdge(int now_, int L_, int R_, int l_, int r_, int id_) {
if (! now_) return ;
if (l_ <= L_ && R_ <= r_) {
Add(id_, now_);
return ;
}
if (l_ <= mid) AddEdge(ls, L_, mid, l_, r_, id_);
if (r_ > mid) AddEdge(rs, mid + 1, R_, l_, r_, id_);
}
#undef ls
#undef rs
#undef mid
}
void Init() {
e_num = 0;
for (int i = 0; i <= node_num; ++ i) {
head[i] = val[i] = into[i] = f[i] = 0;
}
scanf("%s", s + 1);
n = strlen(s + 1);
SA::Init();
na = read();
for (int i = 1; i <= na; ++ i) {
int l_ = read(), r_ = read();
subs[i] = (Str) {l_, r_, r_ - l_ + 1, i};
val[i] = subs[i].lth;
}
nb = read();
for (int i = 1; i <= nb; ++ i) {
int l_ = read(), r_ = read();
subs[na + i] = (Str) {l_, r_, r_ - l_ + 1, na + i};
}
m = read();
for (int i = 1; i <= m; ++ i) {
int u_ = read(), v_ = read();
Add(u_, v_ + na); //Add(read(), read()+na) 会倒着读
}
node_num = na + nb;
}
bool Check(int x_, int y_, int lth_) {
return SA::Lcp(x_, y_) >= lth_;
}
void AddEdgeB(int id_, int now_) {
int pos = SA::rk[subs[id_].l], l_ = pos, r_ = pos; //l_,r_ 初始值
for (int l = 1, r = pos - 1; l <= r; ) {
int mid = (l + r) >> 1;
if (Check(mid, pos, subs[id_].lth)) {
r = mid - 1;
l_ = mid;
} else {
l = mid + 1;
}
}
for (int l = pos + 1, r = n; l <= r; ) {
int mid = (l + r) >> 1;
if (Check(pos, mid, subs[id_].lth)) {
l = mid + 1;
r_ = mid;
} else {
r = mid - 1;
}
}
Hjt::AddEdge(Hjt::root[now_], 1, n, l_, r_, subs[id_].id);
}
void Build() {
node_num = na + nb;
std::sort(subs + 1, subs + na + nb + 1, cmp);
for (int now = 0, i = 1; i <= na + nb; ++ i) {
if (subs[i].id > na) {
AddEdgeB(i, now);
continue;
}
++ now;
Hjt::Insert(Hjt::root[now], Hjt::root[now - 1], 1, n, SA::rk[subs[i].l],
subs[i].id);
}
}
void TopSort() {
std::queue <int> q;
for (int i = 1; i <= node_num; ++ i) {
if (!into[i]) {
f[i] = val[i];
q.push(i);
}
}
while (! q.empty()) {
int u_ = q.front(); q.pop();
for (int i = head[u_]; i; i = ne[i]) {
int v_ = v[i];
Chkmax(f[v_], f[u_] + val[v_]);
-- into[v_];
if (!into[v_]) q.push(v_);
}
}
LL ans = 0;
for (int i = 1; i <= node_num; ++ i) {
Chkmax(ans, f[i]);
if (into[i]) {
printf("-1\n");
return ;
}
}
printf("%lld\n", ans);
}
//=============================================================
int main() {
int T = read();
while (T --) {
Init();
Build();
TopSort();
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号